基于“学习即研究”观点的核心素养培养策略

吴 敏 刘霁华

(1. 江苏省常州市第二中学,江苏 常州 213003; 2. 江苏省常州市教育科学研究院，江苏 常州 213001)

物理观念、科学思维、科学探究、科学态度与责任构成了物理学科核心素养的4大方面．所以“素养不只是知识与技能,它是在特定情境中、通过利用和调动心理和社会资源(包括技能和态度)、以满足复杂需要的能力”．要培养学生的核心素养,就要在教学中立足学生主体,全面发展学生的学科能力、必备品格和价值观念．那么在物理课堂上如何体现核心素养培养的要求呢?

1 “学习即研究”观点

“学习即研究”观点”[1]认为:科学学习的本质是研究,学习者就是研究者,学习过程就是研究过程．这个过程要依据学生的真实思维、构建真实的情境、以问题为纽带、实现过程的体验和和方法的运用,并在质疑评价中推进研究成果的深入和发展．学习的目的包含研究本身,不惟结论、不拘形式．这一观点确立了学生的主体地位,特显了学习的本质,为当前核心素养的培养提供了有效策略．

2 “学习即研究”观点的核心素养培养策略

按照“学习即研究”观点,要落实素养培养的要求,就要用研究的观点设计学习、用研究的方式组织学习、用研究的过程深化学习、用研究的文化丰富学习．下面以江苏省高中物理优课一等奖《动量 动量定理》为例来谈谈“学习即研究观点”下的具体的做法,以期和同行们共同交流．

2.1 体现研究的选择性——回归物理学的学科本质

素养培养的课堂,要选择能促进素养发展的内容在课堂开展讨论,这里最重要的途径就是回归本质．本质中包含着理性思维的魅力、过程与方法的精妙、求真求美的精神,是培养学生科学观念、科学思维、科学探究和科学态度等核心素养的最重要素材．只有在本质中才能体验科学思维的过程、促进物理观念的形成,在知识层面则由知道上升为领悟．但本质具有隐蔽性、复杂性、抽象性,对本质的学习需要教师的挖掘和设计．如本节选择的“动量是矢量”的教学设计如下.

师:动量是矢量还是标量?(研究问题1)

生:矢量,因为速度是矢量．(此时学生处在“知道”的水平)

师:为什么动量定义成质量与速度的乘积?为什么不像动能那样,v指的是速度的大小呢?

生:……(疑惑,在本质性的问题面前产生了思维冲突,引发了问题的研究)

师:展现二维碰撞的实验视频和合成的频闪照片(图1)．引导学生理解在时间间隔相等的情况下用距离来替代速度的大小,从而计算出碰撞前后的动量,画出动量的图示(图2),很快就发现前后动量之和不变满足的是平行四边形定则(图3)．

图1

图2 图3

生:哦,原来动量果真是失量!(知其然更知其所以然——碰撞中动量这个不变量遵循的是矢量的守恒,所以动量才是矢量,这才是动量矢量性的本质! 也许学生内心还能联想到了上节课反方向碰撞要相减,联想到机械能守恒是标量的守恒,所以动能是标量．)

通过对本质的回归,选择了有价值的研究问题,学生获得的不仅是知识结论,而是理论依据和形成过程,这就从原来的知道上升为领悟,感受到了科学方法和严谨态度,实现核心素养多个维度的培养．下面的几个研究的问题也都体现了这种选择性,研究的选择性要注意循序渐进的原则——置疑不等于置难!比如本节课我们并没有对冲量的方向进行复杂的讨论,还是先分析和力的方向一致的简单情况,就是基于这样的考虑．

2.2 体现研究的曲折性——基于学生主体的本位思维

研究的过程不可能是一帆风顺的,忽视学生主体地位、一步到位、包办代替等方式是伪研究的表现,难以实现学生素养的提升．课堂要立足学生的本位思维,把质疑评价等环节引入课堂,体现研究过程的曲折性,促进学生批判性思维的发展．本节课中推演动量定理的过程就体现了这样的策略.

生:两同学展示头顶足球的表演,其他同学看着兴趣盎然．

师:在顶球的过程中,足球的动量变化了吗?

生:变化了．

师:请顶球的同学说说他的头部感受．

生:有点疼! (笑)

师:请用物理的语言表达“有点疼”．

生:有力的作用．

师:对!那么力与动量变化有什么关系?(研究问题2)

建立模型(如图4所示):

图4

理论推导:F=ma=m(v2-v1)/t.

得出结论:Ft=mv2-mv1.

质疑评价:同学们讨论,对上述研究过程有疑问吗?

生:如果不光滑、力的方向和速度方向不一致或者变力情况怎么办呢?

师:非常好!不光滑,这要把上述恒力看成是合力就解决了;如力的方向和运动方向不一致,我们在前面讨论动量的矢量性的实验中已经看到,这时动量变化应该用平行四边形法则处理．变力,其实前面同学头顶球的力就是变力．

师:那么变力与动量变化有什么关系?(研究问题3),结合过去的学习经验,思考一下变力问题我们如何处理?

生:把时间分割成一小段一小段处理(迁移)．

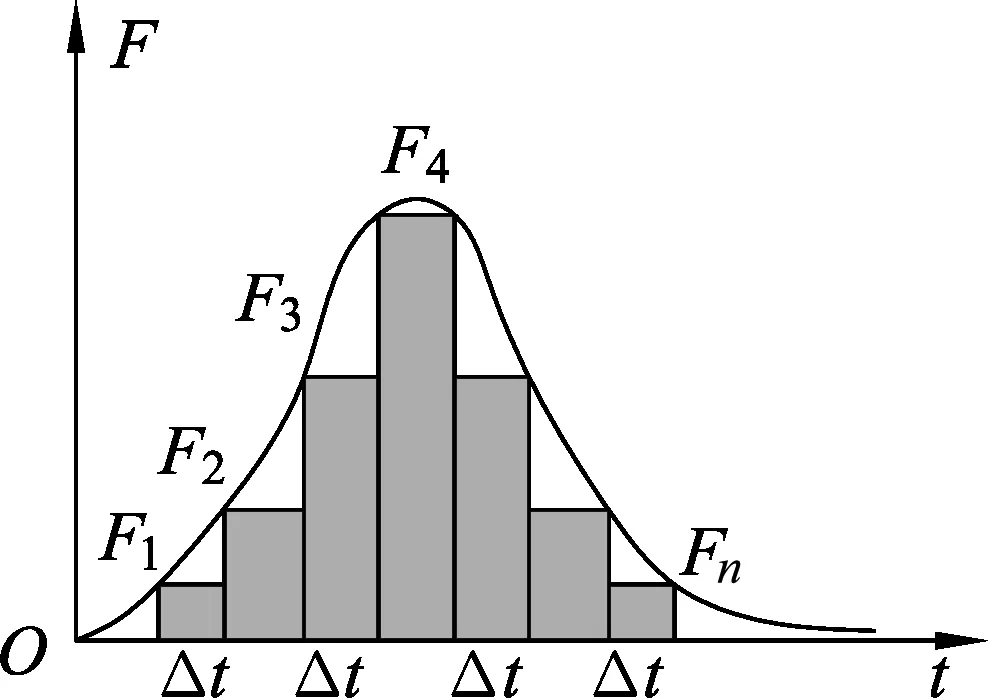
图5

师:根据下面的3幅图(图5—图7),引导学生用微元法逐步进行变力的研究．

图6 图7

如果把时间划分很短,每一小段里就可看成恒力,得到这样的一系列表达式:

F1Δt=mv1-mv0,F2Δt=mv2-mv1,F3Δt=mv3-mv2,……FnΔt=mvn-mvn-1.

把这些式子全部累加起来,就得到这样一个表达式

F1Δt+F2Δt+F3Δt…+FnΔt=mv1-mv0+mv2-mv1+mv3-mv2…+mvn-mvn-1=mvn-mv0.

而F1Δt+F2Δt+…+FnΔt在图像上表示无数个小矩形面积之和,当时间间隔划分得趋于0,就变成了图线与时间轴所围的面积,这个面积叫力与时间乘积的累积(图7)．

得出结论:力(恒力或变力)与时间乘积的累积等于这个过程初末动量的变化．

质疑评价:前面我们由特殊到一般,并利用微元法,等到了一般性的结论,但是理论推导的结果必须通过实验验证,才是可靠的(科学态度)．

实验验证:让一辆229g小车去碰力的传感器,力传感器能采集到碰撞中的实时作用力,用光电门完成对速度的测量(图8),通过朗威8.0版变力与动量变化的关系专用软件采集处理数据,动量变化为0.251kg·m/s,冲量(面积值)为0.252N·s(图9),两者符合的很好．

图8

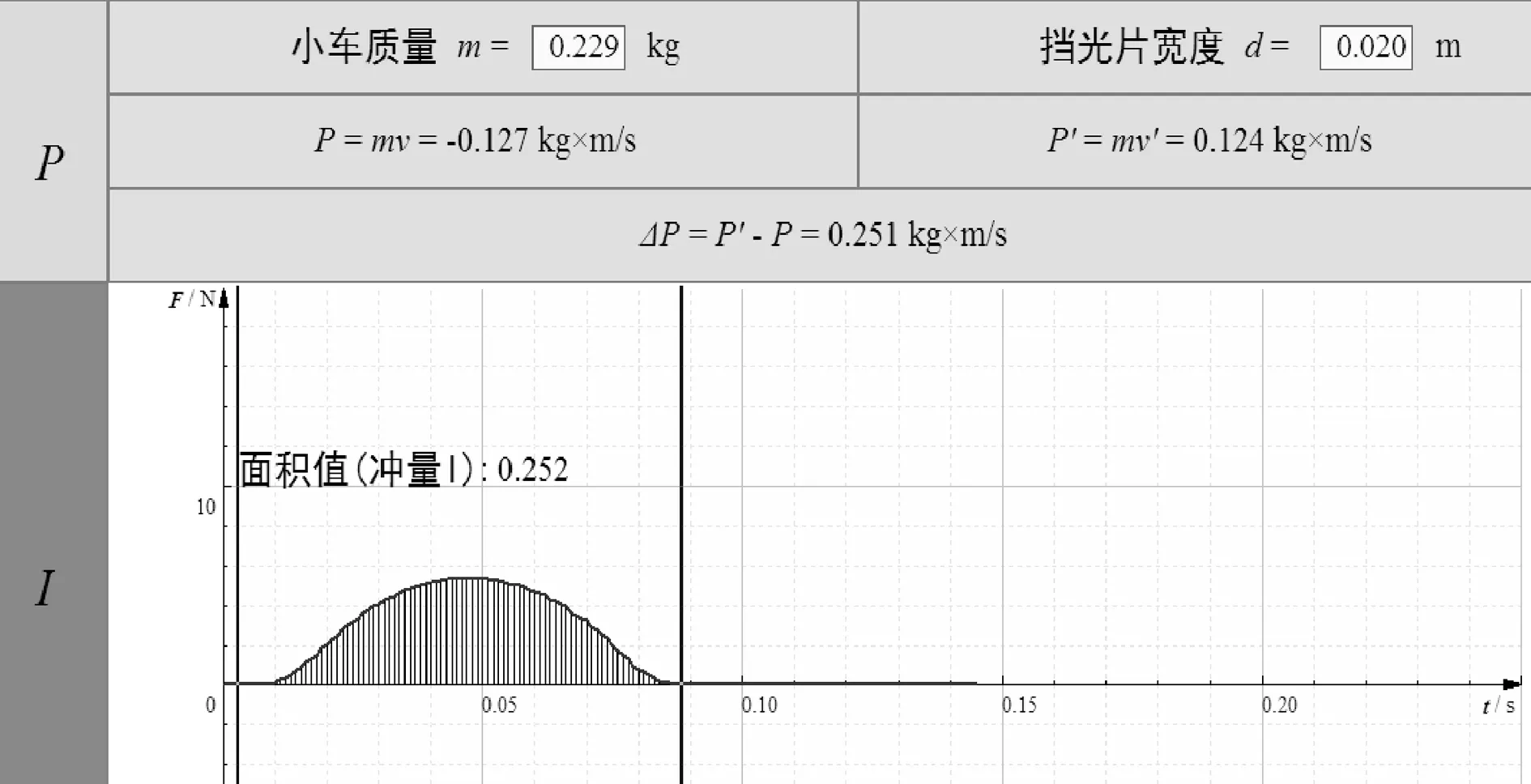
图9

通过质疑评价环节,对特殊条件下获得的结论的质疑,生成出一般条件下的问题;对一般性结论的质疑,生成了理论探究的成果需要通过实验检验的实证思想;展示了研究的曲折过程,体现了思维由浅入深、由表及里的发展过程,将学生的思维引向更高的层次．质疑批判是布鲁姆能力目标的高级层次,因此是培养学生科学探究能力、严谨认真的科学态度等核心素养的重要手段．要想提高学生的科学探究的能力,理应在课堂教学的环节中渗透质疑的意识,批判的精神．

2.3 体现研究的思想性——注重思想方法的渗透与熏陶

物理知识的学习过程,离不开思想方法、程序方法．古人说:“授人以鱼,只供一饭之需,教人以渔,则终身受用无穷”．重视知识与方法的统一性,在教学中渗透思想方法的内容,关注思想方法的习得与领悟,是科学探究能力培养的重要内容．本节课在研究力与动量变化的关系过程中,建立模型、质疑评价、实验验证等步骤,不需要教师过多的讲解,却起到了对学生的科学方法和科学态度的熏陶．使学生认识到科学研究程序的逻辑性,研究过程中显化的微元法、从特殊到一般的研究方法,必然会凝练为学生的核心素养．

2.4 体现研究的人文性——注重物理教学的情感渗透

科学态度与责任,靠灌输难以培养,要依据物理学的学科特点,创设充满人文品味的物理课堂．物理学发展的过程是人类认识世界的过程,物理教学理应展示物理学的文化品位、体现自然的和谐统一．如本节课在讨论动量的矢量性后,笔者给学生介绍了科学家对动量的认识过程及笛卡尔、惠根斯、牛顿在动量概念建立过程中发挥的关键作用,使他们认识到科学探究从来都不是一蹴而就的,科学发展的道路是曲折的．在本节课的结尾,笔者对“力与运动的关系”的讨论也是体现了物理学特有的魅力,激发了学生对自然本真的感悟和对物理学的赞美之情．

师: 力与运动这个看似简单的问题,曾困扰了人们数千年,人们理清力与运动的关系也经历了一个复杂的过程,那么我们学过哪些描述力与运动的关系式?

生:动量定理算一个吧!

师:当然,还有吗?

生:动能定理．

生:牛顿第二定律．

师:总结的很好!动能定理和动量定理都可以从牛顿第二定律推导出来,这3个关系式是否有重复的嫌疑?

生:……

师:它们各自描述问题的角度一样吗?

生:不一样,(恍然)动量定理是从力对时间累积的角度……

师:哦!那动能定理,牛顿第二定理又是从哪个角度?

生:动能定理是从力对空间累积的角度,牛顿第二定律说的是力的瞬时性问题!

师:说的太好了!看来,物理学家对力与运动的关系的认识是多角度,多元化的,这种多元的认知方式使得人类对自然的认识逐步走向全面和深刻!

2.5 体现研究的主体性——落实学生主体的自主参与

“学习即研究”观点认为,学习者即研究者,否则不能称为研究,只能被认为是灌输．物理学习的重要价值是发现,而不是简单的给予．从激疑生趣的鸡蛋砸碎彩钢板的实验开始,到概念的建立,规律的形成,以及运用规律解释实验现象、认识缓冲原理、完成抽桌布实验等研究的过程都是建立在学生的主体需求上的．这个需求不是过去的被动接受,而是通过选择性、参与性、曲折性等过程形成的成就性学习心理的需要．本节课的全过程正是在调动学生的这种需求的基础上完成的,以真正促进学生核心素养的发展．

3 结语

当前教学惟知识、惟书本、惟结论;过程缺失、批判缺失的根本原因与其说是考试等各类评价机制的制约,不如说是广大教师对学习本质缺乏深刻理解,上述案例可以看出,“学习即研究”观点下的教学过程体现了学习过程就是研究过程的学习本质、落实了学习者就是研究者的要求,为当前课堂落实培养学生核心素养的教学目标提供了有效方案和策略．