高中生物理问题表征的差异分析及教学策略

陆永华

(苏州工业园区第二高级中学,江苏 苏州 215000)

问题解决是认知心理学中的核心概念.问题表征是问题解决的关键和研究的核心.问题表征是指把已知的问题转化为内在的心理表象,经过大脑的加工,将内隐的知识外显化.从问题表征到问题解决过程如图1所示,在问题解决过程中,学生由于找到适宜的问题表征而产生顿悟现象,反之在对问题表征不完善或错误的情况下就是试误,需要重新进行表征.

图1

1 物理问题表征

具体学科问题的表征层次虽各不相同,但有共同之处,都认为问题表征可分为高、低两个层次,低层次问题表征以字面理解、表面特征的提取与加工为主,高层次的问题表征则是以问题的内部结构特征和理论范畴为主.物理问题表征既有普通问题表征的共性,又有物理问题的独特个性.物理问题表征模型是基于动力学问题提出来的,主要有两种比较有代表性的观点: (1) 西南师大的廖伯琴教授在著名物理教育家麦克德莫特(McDermott)和拉金(Larkin)提出的物理问题解决表征层次理论基础上,进行了物理问题表征的动态和静态研究,将物理问题表征分为文字表征、朴素表征、物理表征和数学表征四个层次.(2) 南师大的邓铸博士提出中学生物理问题解决是问题表征态不断变化的过程,经历了无表征态、外部表征态、初级内部表征态、低级范畴性表征态、高级范畴性表征态和符号化表征态,这种变化过程具有非线性的、连续的和静态与动态结合的特征.

2 物理问题表征的差异案例举隅

图2

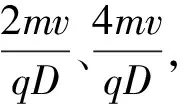
将题意进行不同层次的表征转化如图3所示,题中的图式和数量关系是一种不具形的陈述性知识,不同学生对其表征的差异较大,表征的差异影响学生对解题的顿悟.简言之,问题表征是对问题的一种理解状态,而理解有程度的深浅,因此问题表征就有层次高低的差异.下面以两个高考题的表征为例,对高一和高三年级学生进行横向和纵向的表征差异比较.

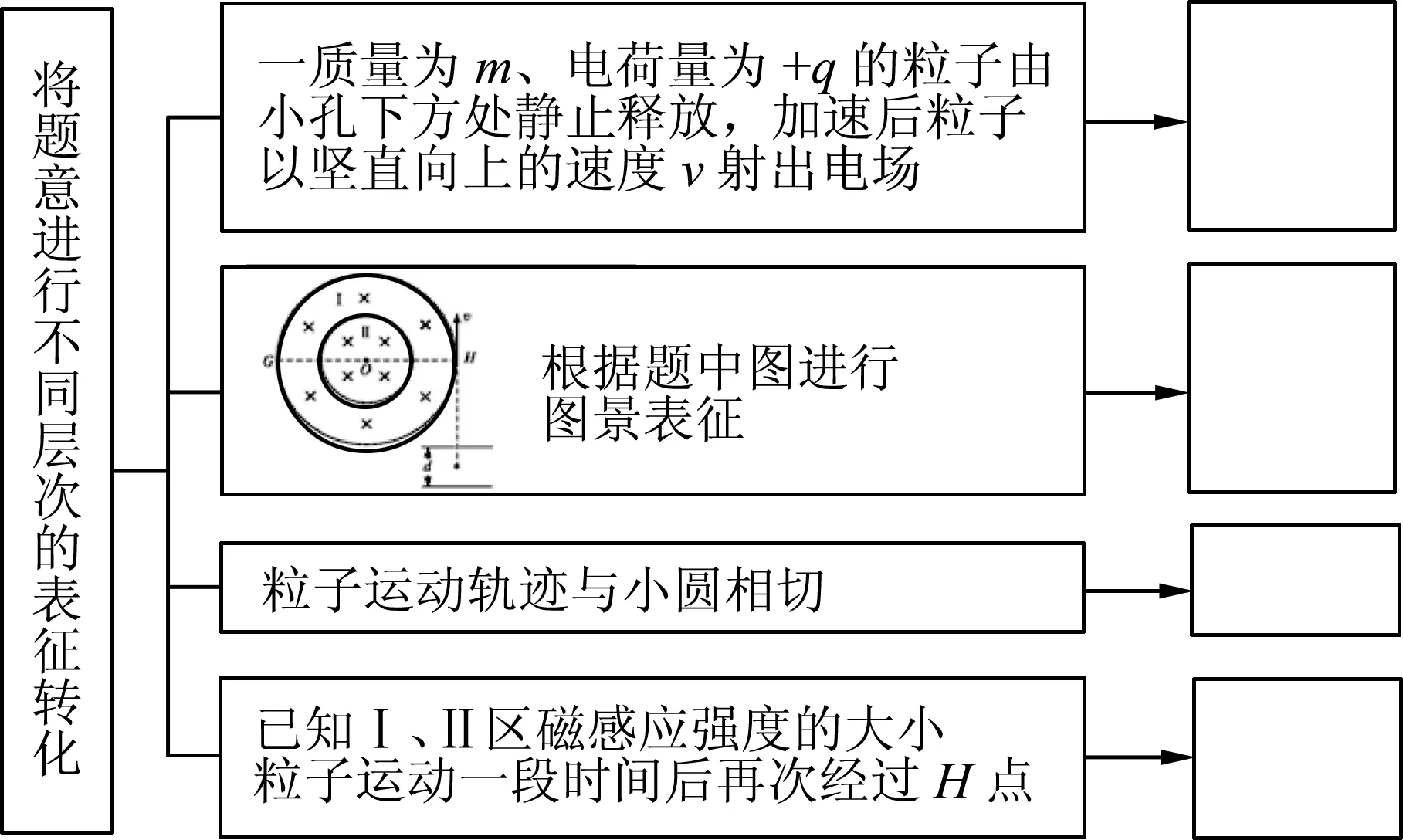
图3 题意的不同层次表征转化

表征案例1.

图4

以2016年四川高考第10题为例:避险车道(图4)是避免恶性交通事故的重要设施,由制动坡床和防撞设施等组成,如图5所示竖直平面内,制动坡床视为与水平面夹角为θ的斜面.一辆长12 m的载有货物的货车因刹车失灵从干道驶入制动坡床,当车速为23 m/s时,车尾位于制动坡床的底端,货物开始在车厢内向车头滑动,当货物在车厢内滑动了4 m时,车头距制动坡床顶端38 m,再过一段时间,货车停止.已知货车质量是货物质量的4倍.货物与车厢间的动摩擦因数为0.4;货车在制动坡床上运动受到的坡床阻力大小为货车和货物总重的0.44倍.货物与货车分别视为小滑块和平板,取cosθ=1,sinθ=0.1,g=10 m/s2.求: (1) 货物在车厢内滑动时加速度的大小和方向; (2) 制动坡床的长度.

图5

以第(1)问为例,表征过程分析如下:对题中的问题表征涉及的陈述性知识: ① 名称或标记知识,如避险车道、制动坡床和防撞设施、货车和车厢等语词知识; ② 事实和有组织论述知识,如货车车长l=12 m,货车质量是货物质量的4倍,货物与车厢间的动摩擦因数为μ=0.4,货车在制动坡床上运动受到的坡床阻力大小为货车和货物总重的0.44倍等.学生所采取的解决策略的关键是产生式系统,将程序性知识条件化:如果已知物体运动情况,那么通过受力分析和牛顿运动定律可求出物体的加速度等情况.处理该类型问题的一般步骤为确定研究对象(外显)→分析运动情况和受力情况(外显)→结合牛顿第二定律F合=ma(外显)→对结果进行验证和对解题过程进行反思(内隐).

学生的表征过程如下.

第1步:题中采用文字表征为主的多元表征,根据题中表述辨认解题情境:驶入制动坡床的货车内的货物与车厢有相对滑动,在头脑中建立题目结构的特征并转化为题给物理条件和所求问题.

第2步:画出货物受力分析图(如图6所示),建立坐标轴,沿制动坡床方向为x轴,垂直于制动坡床方向为y轴,建立“滑块—斜面”物理模型,确认问题整体结构框架,进入朴素表征层次.

图6 图7

上述两步中,有的学生表征过于简单且模糊,无法为物理表征的建立提供基础,如货物与车厢的相对滑动,没有指明具体的运动方向和摩擦力方向等情况.有的学生则在受力分析的画图表征中进一步标注了加速度a和速度v的方向(如图7所示).

第3步:学生的表征差异相对明显,主要有以下几种.

表征1:分别将两个方向范畴表征为匀加速直线运动和滑块平衡,列出下列方程式:

x方向:mgsinθ+f=ma,

y方向:mgcosθ=FN,其中f=μFN.

表征2:首先将受力分析情况分别列出来,

mgcosθ=FN,

Gx=mgsinθ,

Gy=mgcosθ,

按照FN→f→F合→a的思路顺序,

FN=mgcosθ,

f=μFN,

F合=mgsinθ+f,

F合=ma.

表征3:根据题中描述的问题情境,把沿制动坡床方向表征为匀减速直线运动,结合牛顿第二定律公式直接列方程:mgsinθ+μmgcosθ=ma.

第四步:得出加速度a的表达式,将cosθ=0.1,sinθ=0.1,μ=0.4,g=10 m/s2代入计算,并写明a的方向,达到完全表征状态.

表征案例2.

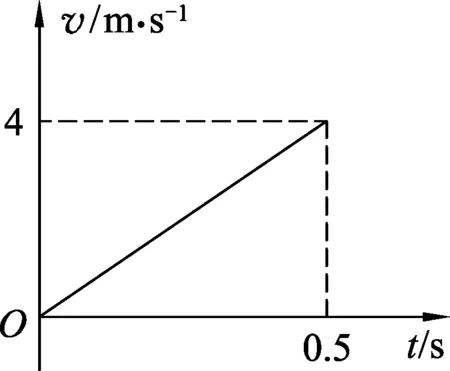
图8

以2012年安徽高考第22题为例:质量为0.1 kg的弹性球从空中某高度由静止开始下落,该下落过程对应的v-t图像如图8所示.球与水平地面相碰后离开地面时的速度大小为碰撞前的3/4.该球受到的空气阻力大小恒为f,取g=10 m/s2,求: (1) 弹性球受到的空气阻力f的大小; (2) 弹性球第一次碰撞后反弹的高度h.

第(1)问主要有两类表征:

第1类表征(逆向推理):要求f,首先要受力分析和运动分析,作出图9受力分析,根据牛顿第二定律得，mg-f=ma1,其中a1未知.

f=m(g-a1)=0.2 N.

第2类表征(顺向推理):

图9

作出图9受力分析,根据牛顿第二定律得

mg-f=ma1,

f=m(g-a1)=0.2 N.

第1类表征:第一次离开地面后,设上升过程中球的加速度大小为a2,则

mg+f=ma2,a2=12 m/s2.

第2类表征:根据动能定理W合=ΔEk，

得

在上述表征过程中,部分学生在(1)、(2)问中的画图表征受力分析如图10所示,小部分学生画出图11所示的运动过程示意图辅助表征问题.

图10 图11

3 物理问题表征差异的案例分析

认知心理学家认为,问题解决过程就是学习者不断地运用知识对问题进行表征转换与重构,直至问题最终被解决.一般问题解决可以运用多种形式进行表征,学生在解决物理问题的过程中,习惯于以自身具有的物理认知结构去表征并解决问题.不同年级学生的表征差异,除了学生原有物理认知结构的层次差异,还在于在深层表征上不能有效的实现多种不同表征方式之间的转换,缺乏对问题解决过程的有意识监控.

根据上述两例表征案例,学生在解决问题时,主要采用盲目试误法和原理统率两种典型策略,高一学生多采用盲目试误策略,更多地依赖于产生式系统(如果……那么……),且主要采用逆向推理解决策略,这种策略更多地依赖于公式的推导,朝着认知目标层层推进,最后解决问题.高三学生部分倾向于顺向推理解决问题,多数采用了原理统率策略,依据相关原理对物理问题先进行表征,然后解决问题.运用顺向推理策略解决问题,相比于运用逆向推理策略,更有利于学生获得问题的图式.

在表征案例1的具有明显表征差异的“第3步”中,表征1采取内隐表征的问题表征策略,内隐表征是在头脑中进行表征分析,从而形成问题解决的框架结构,从认知作业上说明此类学生已经了解子问题空间的相互依赖性.表征2采取的是层层推进式,表征过程较为复杂,此类学生把有限的工作记忆陷入繁琐的计算中,容易在问题表征转换过程中由于信息遗漏、信息误解而发生表征错误,达不到对问题的完全表征.表征3水平较高,直接在脑海中进行两个方向的空间表征,几乎同时进行了物理表征和数学表征.

在表征案例2的第(1)问中,高三学生偏于顺推策略,高一学生偏于逆推策略.第(2)问中,高一和高三均有部分学生(均已学过动能定理)仍采用采用动力学方法解决问题.学生对此类问题的表征来源于心理学中的“问题情境功能固着”,即学生习惯于把问题置于自己最熟悉的情境中去表征,反映出这些学生在物理认知结构的建构上的滞后性,没有建立物理知识整体框架的良好组织程度.在这些学生大脑中,动力学方法比动能定理具有相对优势兴奋性,优先被激活.

在上述两个表征案例中,画图表征值得注意,画图表征在物理问题解决中起着十分重要的作用.现代认知心理学认为一个人的工作记忆容量有限,而示意图具有简明、清晰、形象、信息量大等特点,有助于建立清晰有序的物理过程,帮助学生形成对问题的正确表征.

4 提高物理问题表征能力的教学策略

4.1 通过借助外在表征提高物理问题表征能力

问题表征在形式上分为内在表征和外在表征两种.外在问题表征有助于在一个整体情境下建构问题的框架,将问题与学生的原有认知建立沟通.外在表征能有效减轻大脑的负担,提高解决问题的效率.在物理问题表征过程中,运用文字符号、图形、模型、实验等外部表征的方法简化对问题的思考,使问题的研究对象、状态过程清晰显现出来,让问题明朗化、模型化,从而理顺物理问题的复杂关系.

学生无法实现问题解决的关键常在于表征问题时不能有效地在几种表征方式之间进行转换.由此,教师在平时教学中应该培养学生借助于外在表征形式表征问题的习惯,以促进其合理地表征问题.在解决问题过程中,引导学生用自己的语言转述题意(文字表征),对问题进行画图表征,根据模式特征搜索出必要的物理概念、规律,将概念、规律和表象有机结合,经过科学抽象后建构物理情境和物理模型,尽可能地从不同方式进行表征,帮助学生建构起相应的心理意义,使学生在潜移默化中养成借助于外在表征去表征问题的习惯.

4.2 通过构建丰富图式提高物理问题表征能力

在问题解决中常有“一听就懂,一看就会,一做就错”的现象,说明从知识到能力,从解题操作到问题解决技能,有一个不可或缺的心理历程,即形成合理的知识组块、建立问题解决的图式．认知心理学中的图式是一种由主体已往的经验所形成的关于某一常见的、复杂的概念或问题或现象的记忆组块.

在问题解决研究领域中,研究者证实“脑中一定储存有解决并组织问题的响应图式”,优生能应用已有的丰富“感知块”及高度概括的认知分枝对问题进行一系列不同层次的表征.高三学生的认知结构相对比较完整,脑中有大量的图式以知识组块的形式存在.例如“表征案例1”中,当审题完毕进行受力分析后,就能提取脑中存在的“力的分解”的图式,并在脑海中形成清晰的空间表征,继而把问题纳入一定的范畴,选用物理公式,直接进入物理表征和数学表征,最后将已知条件代入计算,实现对问题的完全表征.与图式关联的一般问题解决模式如图12所示.

图12

一个问题图式包含两部分信息:其一是关于它所对应的某类问题的特征描述,其二是该类问题的解决方法和程序.图式与某类问题匹配,一旦激活匹配该问题图式即可自动表征问题并执行相应的解题程序,努力少、步骤省、解题快,例如“导体棒平动切割磁感线时所受的安培力具体表达式”模型图式,如图13所示.

图13

样例教学是丰富学生头脑中的相关问题图式的重要途径.在物理样例教学中,通过系列物理样例问题训练学生,使学生在样例问题解决过程中掌握问题规则和强化对条件的认知能力,丰富和完善学生有关物理问题解决思想和方法的认知样例.当遇到新问题时,按照样例学习中建立的产生式对问题线索和规则进行认知和表征,帮助学生在表征问题过程中快而准的模式识别,从而提高问题表征能力.

4.3 通过编撰物理习题提高物理问题表征能力

物理习题是由一个或若干个学科原理,以一个或若干个能承载学科原理的物理情境,将学科原理中所涉及的某些物理量或物理量之间存在的某些内在联系以间接的表征方式予以呈现,进而构成具有“知识锁链脱节”特征的物理问题.成品的物理习题已经由命题者经过简化抽象的精心打磨,认知训练过程已经被命题者“越俎代庖”,导致学生的“知识与认知锁链的脱节”.若反其道而行之,教师引导帮助学生自行编撰物理习题,如图14所示,通过表征问题训练,使学生进一步理解物理问题是如何构造的,让学生对生活中的物理现象、过程与物理知识之间的联系能够更深入地理解,让学生活化长时记忆中的物理知识组块,从而提高解决物理问题的能力.

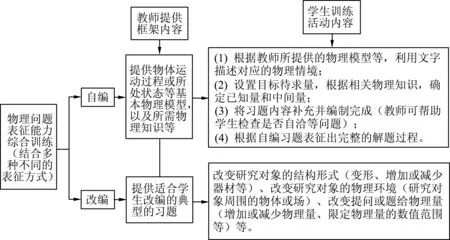
图14

4.4 通过问题解决中的元认知训练提高物理问题表征能力

元认知是对认知的认知,既是静态的认知现象,也是动态的认知过程.元认知过程是指导、调节的认知过程,选择有效认知策略的控制执行过程.元认知主要包括元认知知识、元认知体验和元认知监控三大因素,三者相互联系、影响和制约,有机结合构成一个统一整体.丰富元认知知识是提高元认知水平的前提,物理元认知知识从物理认知结构分析,包括物理经验性知识和物理前提性知识.物理学习中的元认知体验,调动非智力因素参与,产生“知”与“不知”的认知体验和情感体验.元认知的监控是通过元认知知识和元认知体验的交互作用来实现的,它贯穿于问题解决过程的始终.物理认知活动中的元认知监控的关键是三个意识,即目标意识(监控认知方向)、自控意识(监控认知进程)、策略意识(调节认知策略).与元认知相结合的解决物理问题的一般过程如图15所示．在问题解决过程中,学生依据原有的元认知知识审题表征相关问题,在实施问题解决过程中,则不断对问题进行积极、自觉的监控,产生问题表征的元认知体验,通过已有的认知体验对元认知监控进行反馈,元认知监控又在后续的实施过程中进行监控,并通过元认知体验对元认知监控的再次反馈进行调节,通过物理元认知的参与,把这些元认知体验同化到学生原有的物理认知结构中去,实现学习策略的迁移,进而促进物理问题的顺利解决.

图15

问题表征对问题能否顺利解决起着至关重要的作用.问题表征不只是一个环节和阶段,而是涵盖从呈现问题到解决问题,贯穿问题解决过程始终的动态认知过程,但问题表征层次之间并不都是呈线性关系的,经常会发生跳跃或重叠.研究学生解决物理问题过程中的问题表征,在问题解决过程中发现问题理解与表征上存在的不足,有助于为物理教学实践中扭转教师教学“不自觉”的“经验状态”提供理论基础,从而提高教学质量,更好的为培养学生的物理核心素养而服务.