基于粗糙集的数据流多标记分布特征选择
程玉胜,陈 飞,王一宾,2
(1.安庆师范大学 计算机与信息学院,安徽 安庆 246011; 2.安徽省智能感知与计算重点实验室, 安徽 安庆 246011; 3. 数据科学与智能应用福建省高校重点实验室,福建 漳州 363000)(*通信作者电子邮箱chengyshaq@163.com)
0 引言
多标记学习作为机器学习研究热点,对现实世界中多义性对象的研究具有重要意义[1],并且多标记学习对象在日常生活中广泛存在。在多标记学习框架之下,数据往往面临多标记性和高维性等多种问题,使得手工标记一般费时费力。同时随着数据维数的不断增加,分类器的分类精度也在不断下降,因此探究高效的分类算法就显得尤为重要。近年来,相关学者在此问题上的研究已经取得了卓越的成绩,提出了多种算法[2-5]。在现有的多标记分类算法中,与实例相关的标记重要程度被视作相同,然而在现实世界中,不同的标记对于同一个实例的描述程度并不都是相同的。例如在一幅自然风景图中,如果出现大量的“蓝天”,那么出现大量“白云”的概率也就高,其他标记的可能性也就比较低,这种现象被称为标记的不平衡性。针对这种标记的不平衡性,Geng等[6]提出了一种标记分布学习(Label Distribution Learning, LDL)范式,将传统的逻辑标记用概率分布的形式来进行描述,更加准确地反映了实例的相关内容。目前也有很多学者在标记分布学习范式下对人年龄[7-8]、人脸面部识别[9]、文本情感分类[10]等领域进行研究。
然而,无论是传统的多标记学习还是标记分布学习,其特征选择方法都假定从一开始就可以获得所有实例的特征数据。但是在许多情况下,往往无法一次性获取实例的所有特征数据,更多呈现动态生成并记录相应特征数据,这种情况获取的特征称为流特征,相应的特征选择算法称为流特征选择算法[11]。例如,对一篇小说进行分类并标上标记,需要提取小说里面所有的高频词特征。如果小说的篇幅比较长则提取所有特征就需要耗费大量的时间,等所有的特征全部提取完之后再进行分类训练是不可能的,更可取的方法是一次一个地生成候选特征,从生成的候选特征中选择特征集合较小并且分类效果也好的特征集合作为最后的特征,这种做法不仅会节省大量的资源,同时分类精度也得到了保证。基于此,Wu等[11]提出了在线流特征选择(Online Streaming Feature Selection, OSFS), 通过对特征的相关性和冗余性进行分析,得到满足条件的特征集合,并在文献[12]中设计出了一系列的算法,取得了十分明显的效果。但是,文献[12]中所提到的算法主要适用于离散的数据,且为单个逻辑标记的数据集,对于多个逻辑标记及其标记分布并不适用。
另外,上述算法无论是逻辑标记还是标记分布,在对特征进行选择时考虑更多的是特征与标记之间的相关性,如:张振海等[13]利用信息熵进行多标记的特征选择;Lee等[4]提出一种使用多变量互信息对特征进行选择,但对特征之间的冗余性考虑不充分,属性约简不够充分。OSFS虽然考虑了特征间的冗余性,但计算过程较为复杂,算法效率较低,而粗糙集最大的贡献就是进行属性约简,去除冗余属性。
粗糙集理论是Pawlak[14]提出的一种处理不精确、不确定的数学工具,自提出以来在人工智能、机器学习、数据挖掘等领域得到了成功应用。相较于其他的特征选择算法,粗糙集方法不需要先验知识,仅仅利用数据本身所提供的信息发现问题的规律[15],计算过程简单高效。粗糙集理论通过构建上下近似来对知识进行描述,通过下近似与全体论域之间的比值来刻画属性的依赖度从而判断属性的冗余性。一般来说,下近似越大,属性间的依赖度越大,冗余性也就越大。目前利用粗糙集进行属性约简和特征选择是多标记学习的一个热点,Yu等[16-17]将粗糙集的扩展邻域粗糙集应用在多标记分类问题上,取得了显著的成绩;段洁等[18]利用邻域粗糙集实现了多标记分类任务的特征选择算法。但上述算法都应用在逻辑标记且特征数据是静态的环境下,对现实世界中的数据流的情况并不适用。
目前,针对流特征数据的研究更加具有现实意义,同时,标记分布比传统的逻辑标记更能反映样本标记的真实情况。由此,本文提出了基于粗糙集的数据流多标记分布特征选择(multi-label Distribution learning Feature Selection with Streaming Data Using Rough Set, FSSRS)算法。首先将在线特征选择算法应用在多标记学习框架之下,其次将传统的逻辑标记转换成标记分布形式进行学习,同时利用粗糙集中的依赖度来度量特征之间的相关性,从而去除冗余属性,保证最终的特征子集的分类效果。实验结果表明该方法是有效的。
1 相关工作
1.1 传统多标记学习
多标记学习是针对现实生活中普遍存在的多义性对象而提出的一种学习框架,在这个框架之下,样本由多个特征和多个标记构成,学习的目的是将未知的实例对应上更多正确的标记[19]。假设T是含有n个特征的特征集合T={t1,t2,…,tn},L是由m个标记组成的标记集合L={l1,l2,…,lm},其中1表示有该标记,而-1表示没有该标记,则含有i个样本的多标记数据集可以表示为:
D={(Tj,Lj)|1≤j≤i,Tj∈T,Lj∈L}
(1)
1.2 标记分布学习

1.3 数据流特征选择
传统的多标记学习中,所有实例的特征数据都是完整的,并可以一次性获得,从而进行相应的分类学习。但是,在一些情况下,同一实例的不同特征数据往往是实时生成并记录的,并且这些特征的生成是无序的,有些特征数据甚至是无穷的。如果用传统的多标记特征选择算法无疑会浪费大量的时间和精力,对于那些特征数据是无穷的实例,传统方法更是无法进行特征选择。解决这个问题最好的方法就是从实时产生的特征数据中选择符合一定条件的特征构成候选特征子集,利用这个特征子集进行相应的训练和测试,这种方法被称为在线流特征选择(OSFS)[11]。在OSFS框架之下,对特征子集的选择标准总共分成两部分:1)特征与标记之间相关性;2)特征与特征之间的冗余性。根据上述两种情况,候选的特征集合又可以分为以下4个部分:1)不相关的特征;2)强相关的特征;3)弱相关非冗余特征;4)弱相关冗余特征。
通过计算特征与标记之间的相关性舍弃不相关特征并保留强相关特征,对于弱相关的特征再进行特征之间冗余性判断,舍弃冗余属性。由此,最终的特征子集应包括强相关特征和弱相关但非冗余特征。
1.4 粗糙集理论
粗糙集理论是一种处理不精确、不确定的数学工具,自提出便广泛应用到人工智能、机器学习等领域。在粗糙集理论中,对于一个信息系统IS=〈U,Q,V,f〉,其中:U表示全体论域,即样本集合;Q表示属性集合(包括条件属性C和决策属性D);V表示属性的值域;f表示一种映射。在分类过程中,差别不大的样本被划成一类,它们的关系被称为相容关系或者等价关系。为方便问题描述,本文仅仅考虑了等价关系。对于任何一个属性集合C,其等价关系可以用下面不可分辨关系IND来表示,定义如下:
IND(C)={(x,y)∈U×U:f(x,a)=f(y,a),a∈C}
(2)
不可分辨关系也就是U上的等价关系,可以用U/C来表示。粗糙集理论中,用上下近似来对知识进行描述,假设B⊆C,X⊆U,则B的上近似与B的下近似定义如下:
∅}
(3)

(4)
通过上下近似可以定义正域(POS)、负域(NEG)和边界域(BNG):
(5)
(6)
(7)
发现属性之间的依赖关系也是数据分析中十分重要的一个问题。在粗糙集理论中,可以利用依赖度(Dep)来表示两个属性之间的依赖程度。假设B⊆C,则决策属性D对条件属性B的依赖程度用式(8)进行计算:
(8)
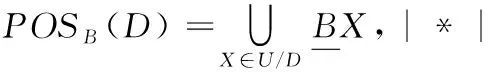


表1 粗糙集示例
2 数据流多标记分布特征选择算法
2.1 特征与标记的相关性
在多标记学习框架之下,标记的准确性常常与特征的个数有着密切的联系。在一定的范围内特征越多标记准确性也就越高,但随着特征数目的不断增加,次要特征和冗余特征也随之增多,这就会导致分类器的精度下降,所以选择与标记相关的特征就显得尤为重要。在目前的多标记特征选择中,大多数学者利用信息熵来度量特征与标记之间的相关性,选择信息熵较大的特征作为重要特征[20-22],但是,传统的信息熵只能处理离散型数据,对于标记分布中标记空间的连续型概率分布数据并不适用。
在统计学中,皮尔逊相关系数(Pearson)常常用于度量两个连续变量X和Y之间的相关性,其值为-1~1。其中正值表示正相关,反之则为负相关;皮尔逊相关系数绝对值越大则表示两个变量的相关性越大。并且规定,若相关系数大于0.6则为强相关,相关系数小于0.2则为弱相关或不相关[23]。皮尔逊相关系数可以通过式(9)进行计算:
(9)
其中:E表示数学期望,Cov表示协方差。
2.2 特征之间的冗余性
在传统的OSFS框架[11]之下,往往是利用特征与标记之间的条件概率对特征的冗余性进行判断,对于特征X、S和标记T,如果P(T|X,S)=P(T|S),则表示特征X对标记T是冗余的。这种判断方法需要知道特征空间、标记空间和每个特征的先验知识且计算复杂,而粗糙集方法可以很好地解决这个问题。在粗糙集理论中,条件属性与决策属性之间的依赖度可以很好地刻画两者之间的依赖程度。将依赖度引入到特征选择中对两个特征之间进行冗余性判断。计算流入特征与已确定特征之间的依赖度,若两者依赖度越大,独立性越小,冗余性也就越大。
2.3 基于粗糙集的数据流多标记分布特征选择
FSSRS算法对于实时产生的特征数据进行十折离散化[24],利用皮尔逊相关系数对特征与标记之间的相关性进行判断,对于强相关的特征直接保留进入最终的特征子集中,不相关的特征则直接舍弃,弱相关的特征暂时保留在弱相关子集中,在下一个弱相关特征流入时进行冗余性判断。
对于流入的弱相关特征,与弱相关子集中的特征利用式(8)计算冗余性,将冗余的属性直接舍弃,在保证分类器精度的同时也确保了最小的特征子集。
由于数据是实时产生并记录的,需要提前设置好相关参数:α为强相关系数,β为不相关系数,γ为冗余性系数。
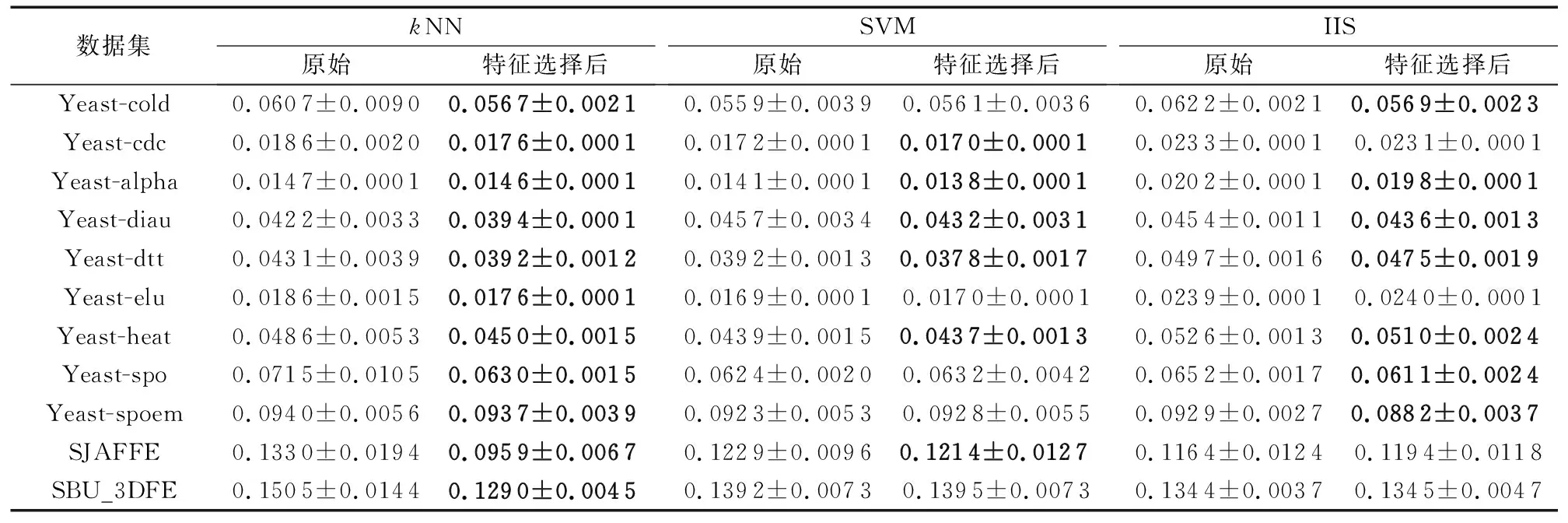
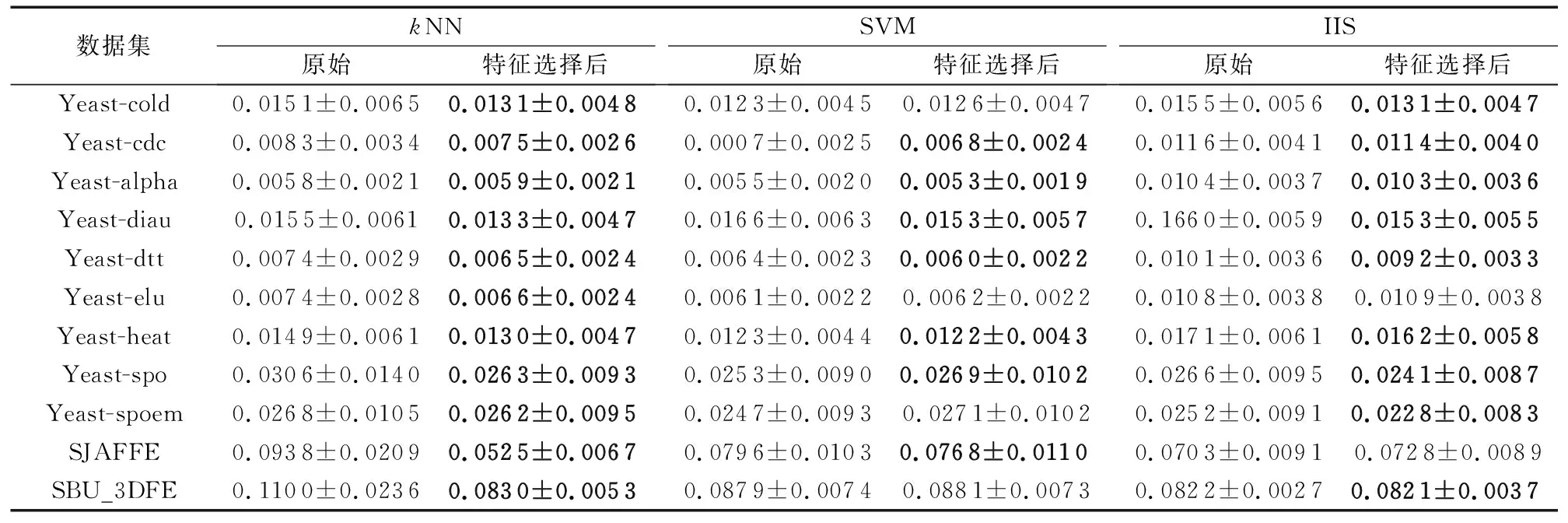
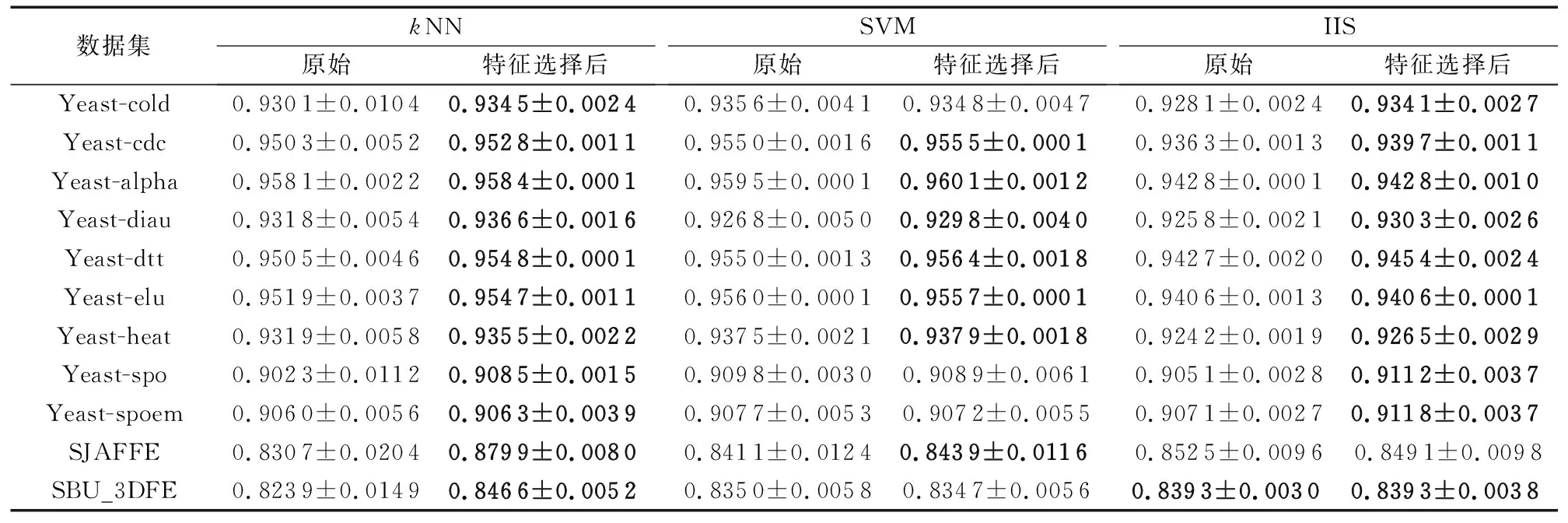
在线特征相关性 在t时刻获取特征fti,利用皮尔逊相关系数进行计算特征与标记的相关性计算: 如果Pearsonti≥α则为强相关性特征,直接存到最终的特征子集中; 如果Pearsonti≤β则为不相关特征直接舍弃,如果α 在线特征冗余性 对于暂时保留的特征fti,利用式(8)计算与ti-1时刻确定的最终特征子集进行依赖度计算,如果Depti≤γ则表示没有冗余性,该特征存到最终特征子集中,否则舍弃该特征。 通过相关性与冗余性的判断之后输出最终的特征子集,并利用此特征子集进行训练与测试。该算法的伪代码如下所示: 算法 基于粗糙集的数据流多标记分布特征选择。 输入fti为ti时刻的特征数据,α为强相关系数,β为不相关系数,γ为冗余性系数。 输出 选择后的特征子集FS。 1) repeat 2) 在ti时刻得到一个新的特征数据fti; 3) 利用皮尔逊相关系数计算t时刻的相关性Pearsonti; 4) IFPearsonti≥α 5) 将fti加入到FS中; 6) 跳转到步骤17); 7) ELSE IFPearsonti≤β 8) 舍弃fti; 9) ELSE 10) 利用式(8)计算特征间的依赖度Depti; 11) IFDepti≤γ 12) 将fti加入到FS中; 13) Else 14) 舍弃fti; 15) End IF并跳转到步骤17); 16) End IF并跳转到步骤17); 17) 直到没有新的特征流入; 18) 输出特征子集FS 算法流程如图1所示。 图1 FSSRS算法流程 1)Chebyshev距离(↓): 2)Clark距离(↓): 3)Canberra距离(↓): 4)KL-div散度(↓): 5)Cosine相似度(↑): 6)Intersection相似度(↑): 本文所有实验均运行在3.4 GHz处理器,8.00 GB内存及Matlab R2016a的实验平台上。实验数据来源于标记分布常用数据集(http://ldl.herokuapp.com/download),选取其中12个数据集进行对比实验,其基本信息如表2所示。 为验证算法的有效性,与耿新提出的AA-kNN (Algorithm Adaptationk-Nearest Neighbors)、PT-SVM (Problem Transformation SVM)和SA-IIS(Specialized Algorithm Improved Iterative Scaling)进行对比,对比实验采用10折交叉验证。表2中也列出了各数据集特征选择的数量,表3~8则给出了11个数据集在三种不同算法上的实验结果(平均值±标准差), 实验中,α=0.8,β=0.3,γ=0.5。表9和表10是在Yeast-dtt数据集上,分类器选择kNN,当γ=0.5时,α、β不同取值时的结果(说明:表中黑色加粗的数字表示在该指标上特征选择后的数据优于原始数据;数据括号中的数字为该值在评价指标中的排名情况)。 表3 Chebyshev实验结果 表4 Clark实验结果 表5 Canberra实验结果 表6 Kullback-Leibler实验结果 表7 Cosine实验结果 表8 Intersection实验结果 表9 Yeast-dtt数据集不同参数实验结果 (β=0.3,γ=0.5) 表10 Yeast-dtt数据集不同参数实验结果 (β=0.2,γ=0.5) 从实验结果来看,在11个数据集6个评价指标共66个实验结果上,AA-kNN有95.5%的结果优于原始数据,PT-SVM有56.1%的结果优于原始数据,SA-IIS有83.3%的结果优于原始数据。 从表9和表10可知: 当β=0.3时,α=0.7取得更多最优结果; 当β=0.2时,α=0.8取得更多最优结果; 所有特征选择的结果都优于原始数据。 图2~图3是Yeast-cold数据集在不同参数下的实验结果对比。由图2可以看出,特征选择数目与弱相关系数有着密切的关系;由图3可以看出, 经过特征选择后的分类效果要优于原始特征,结果也较为稳定。 针对传统多标记学习框架的逻辑标记和静态特征的情况,提出了基于粗糙集的数据流多标记分布特征选择算法,为了更加准确地对样本进行描述,将传统的逻辑标记转换成概率的形式。同时对实时产生的特征数据利用皮尔逊相关系数与粗糙集中的依赖度进行处理,保留符合条件的特征构成特征子集进行训练,在节约资源的情况下又使得分类精度得到了保证,多组实验证明了该算法的有效性。 图2 不同参数特征选择个数(Yeast-cold) 但是本文仍存在一些问题,如FSSRS算法在进行冗余性判断时,对于已经是强相关性的特征没有进行冗余性检查,以后将对此进行改进;同时本文的参数是人为设定,今后将继续完善参数选择,使得算法更加高效。 图3 Yeast-cold数据集不同参数实验结果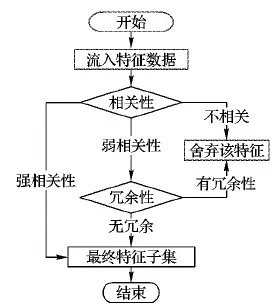
3 实验结果及分析
3.1 评价指标

3.2 实验数据集
3.3 实验结果与分析





4 结语



