刍议微专题在中考数学复习中的应用

☉江苏省高邮市送桥镇送桥初级中学赵正萍

专题复习不应该仅仅只出现在初三数学的二轮复习中，在进行中考一轮复习时，教师同样可以运用微专题帮助学生进行整理，并由此提升他们的能力和水平.

一、微专题在初中数学中考复习中的意义

将微专题应用于初中数学的中考复习，对学生知识的系统化建构，以及相应能力的提升，是很有意义的一件事情.这是由微专题的基本特点决定的.

首先，微专题的范围相对比较小，这也就导致微专题具有极强的针对性，方便学生及时而有效地展开自己的复习.尤其针对学生学习过程中一些遗留下来的重、难点问题，就显得更加有效，微专题的使用可以更加有效地提升学生回忆知识的速度，也有助于他们形成深刻的认识.

其次，微专题能够突出重点，避免学生平均用力，进而让学生能够在短时间内对重点问题进行强化处理，使得学生能够在紧张的初三复习中更加自主地实现对时间的科学安排.教师合理地设计微专题，可以帮助学生从知识、方法和思想等多方面的角度展开复习，由此从横、纵两个方向搭建知识之间的关联，并形成相对稳固的知识体系.而且学生在专题的框架下对知识进行组合，能够达成举一反三的效果.

再次，教师在对微专题进行选题、组织和设计时，都要有意识地将复习策略渗透在其中，引领学生在知识复习的同时能掌握一定的复习方法.这样，随着复习过程的深入，学生不但能够有效掌握本专题所涉及的内容，也能培养一种自发而系统的复习意识，并将相关意识应用于他们的后续学习之中.

二、初中数学微专题的内容确定

作为初三数学最重要的一种复习手段，教师必须明确，不是每一个初中数学的知识点都可以采用微专题的方式进行复习.为了让微专题起到实际效果，教师一定要注意微专题复习的选题，将这种方式使用在其最应该使用的地方.一般来讲，微专题都与综合性的知识学习相关，在数学知识重要的衔接点上，教师采用微专题的方式帮助学生进行复习，能够对知识结构的整体产生更加精确的指向性，学生在此影响下，会逐渐地形成一种自发运用相关知识和方法的意识.

波利亚曾经说过：“相比于知识而言，良好的组织能够让知识发挥实用性，这应该比知识本身更加重要.在很多时候，知识太多反而会显得累赘，它可能在一定程度上妨碍研究者探明问题的解决途径，而良好的组织则有意义得多.”这句话也点明了很多学生在学习数学知识时的一种困境，在刚刚开始学习数学时，他们处理问题时思路相对单一，但是简单直接，随着学习的深入，学生接触的内容变多，思路和方法也更多，他们在处理问题时最大的难点是如何对方法进行选择.因此教师选择微专题的内容时，往往要侧重于章节的衔接之处，即在学生已经有了较为扎实的基础知识复习之后，通过微专题促使他们获得提升和发展.

三、初中数学微专题的课例分析

在学生已经完成对相似三角形的有关内容复习之后，教师可以采用微专题的形式将数学思想融入相关问题的分析和探索之中，由此实现概念的串联，帮助学生将相似三角形与其他问题联系起来，形成更加深刻的认识，同时让自己的思维得到发展.

1.教学过程简介

教师展示两个基本问题.（1）如图1所示的两个三角形△ABC和△DEF存在相似关系吗？请简述原因.（2）如图2所示的两个三角形△ABC和△DEF存在相似关系吗？请简述原因.

图1

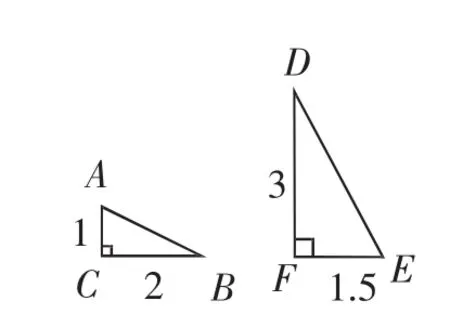
图2

上述两个问题直接衔接学生已经复习过的相似三角形相关内容，教师给出一点时间之后，学生很快给出答案.随后教师进一步提出问题（3）：现有如图3所示的Rt△ABC，其中∠B为直角，两条直角边BC和AB分别等于2和3，请在网格中画出一个直角三角形，即△DEF，以∠D为直角，直角边DE等于6，且要求这个三角形和原先的三角形相似.这是一个操作性很强的问题，通过操作，学生将经历相似三角形的形成过程，由此他们将纠正一些原本较为肤浅的认识.

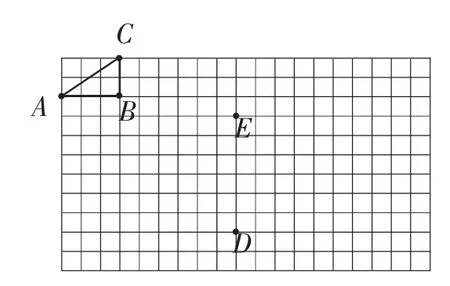
图3

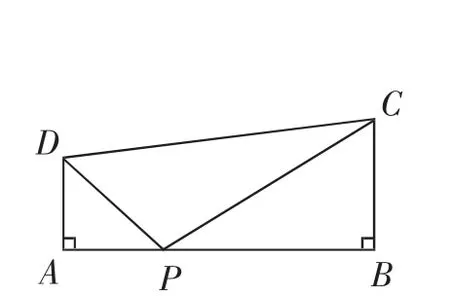
图4

学生的操作过程是一个很耗时间的过程，这时教师要舍得将时间交给学生，鼓励学生在自主操作和辨析中完善认识，并从中积累经验.当学生完成成果展示之后，教师再为学生提供一个新的问题（4）：在如图4所示的四边形ABCD中，已知∠B为直角，且有AD与BC平行，AB等于7，AD等于2，BC等于3，你能否在线段AB上找到点P，使得△PBC和△PAD这两个三角形相似？如果存在，请确定满足条件的点有几个，并求解PA的长度；如果不存在，请说明理由.这个问题兼具操作性和探索性，对学生的能力要求显然更高，这一问题的处理需要教师为学生提供更长的时间，让他们展开探索和研究，并形成属于自己的认识.

在后续环节，教师又安排变式训练，让学生进行技能训练，以便促使学生加深对相关思想的感悟.教师所选择的问题难度绝不能太大，应该切合不同层次学生的需要，整个教学过程中，教师加强了合作学习的引导，让学生在相互启发和探讨中获得解题能力的提升，相关内容在此不再赘述.

2.基本设计思路

从上述教学过程可以看出，微专题的教学是一个逐渐深入的过程.从目标层次设定来看，教师基础性提问中的问题（1）属于了解层次，其后的问题（2）属于理解层次，这两个问题带有一定的预热性质，既让学生能够完成对基本概念的复习，而且能在思想状态上完成准备.而问题（3）具有很强的操作性，对学生的要求已经上升到掌握层次，这个问题能够起到一定的缓冲作用，连接着基础性要求和提升性要求.到了问题（4），就在发展学生应用层面的能力，这个问题本身的难度虽然不大，但是其中蕴含的数学思想不容小觑，比如，其中就蕴含着数形结合、分类讨论、逻辑推理、方程思想等，而且包括一些和几何直观相关的内容.因此，相关问题难度都不大，其目的也不是为了难住学生，教师希望学生能够结合这些问题完成知识梳理，并熟悉最基本的操作方法.

在具体实施的过程中，问题（1）的处理帮助学生解决了相似三角形中最为基础且核心的问题，即三角形的判定.这些问题从表面来看只是让学生回忆“三角形的两边对应成比例，且夹角相等”这一判定定理，但是实际教学中，教师可以结合课堂的实际情况进行变通式的处理，比如，可以在原有问题的基础上继续提问：（1）如果将直角三角形这一条件删掉，结论还成立吗？如果要让结论成立，你能自己补充一些条件吗？（2）如果将图中四条边的长度删掉，结论还成立吗？如果要让结论成立，你能自己补充一些条件吗？这些问题的提出可以让学生对相似三角形的判定定理有一个系统化的复习和整理.

总之，在进行微型专题的设计过程中，教师首先要立足于学生对基础知识和基本技能的掌握，然后谋求进一步的提升和发展.微专题一般以基础性的问题为开始，随着学生的思维被逐步激活，教师要根据实际情况提出一些具有开放性和挑战性的问题，让学生向更深层次发展.此外，在问题的设计中，教师要注意这些问题应该存在一种关联性，即应该让学生经历由易到难的探索过程，并由此建立一条相对明晰的思路，这样的教学有助于学生基础的进一步夯实，而且我们可以由此训练学生的思维，让他们的能力得到切实发展.