暴露思维惯性 提升思维广度 增强解题能力
——以高三三角函数拆角技巧求值复习课为例分析
浙江 陈启超
笔者通过课堂上复习三角函数求值时发现学生对于学过的拆角技巧求值基本不会,大部分学生采用解方程的思想解题.为什么教过的方法学生不会用,而解方程的方法却有那么多的学生采用.从中反思:学生受习惯思维的束缚,按部就班,缺少独立求异的思维,这对学生的发展是不利的.笔者通过对学生学情和教师教学的分析,提了几点突破思维习惯的建议:一是暴露学生原有的思维框架,改善学生的思维习惯;二是加强变式教学,拓展学生思维广度;三是防止解题教学的简单化,提高学生思维深度,与大家共勉.
1.问题提出
在高三的一节三角函数复习课上,笔者给出这样一道题目:
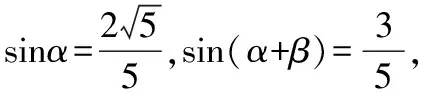
据课堂上观察,学生的做法主要有以下两种:
一种是(很多学生采用的方法)解方程的思想方法:就是利用两角和的正弦公式将sin(α+β)展开,得到sinβ,cosβ的一个关系式,再结合sin2β+cos2β=1去解cosβ.在给定的时间内,很多学生还没算出答案,有的甚至中途放弃了.
另一种是利用拆角的技巧:把β看成是(α+β)-α,则cosβ=cos[(α+β)-α]利用两角差的余弦公式展开计算.但这种方法用的学生很少,一个班就五六位学生左右.
笔者在另外一个班也给出这道题进行试验,结果大致一样,学生大部分选择了解方程的思想.课后,笔者想:拆角的方法思路巧妙,过程简洁,课堂上也讲过这种方法,但为什么过了一段时间后能顺利求解这一问题的学生那么少.这说明平常将看似很好的方法直接灌输给学生,其教学效果是很低的,学生对解题方法的认识只停留在赏析的层面上,没能在大脑中留下深刻的印象,对拆角的方法并没有深刻的理解.我们可以想象,如果下次再出现类似的题目,还是有很多学生用解方程的方法.好的方法学生不会用,为什么会如此? 这是值得思考的一个问题.
2.原因分析
2.1 学生的想法
课后笔者找了几位学生谈心,经过访谈了解到学生的一些想法.
甲同学认为(基础较好):平时在求解三角函数值时经常是利用同角三角函数关系式求解,大部分就是解方程的方法.一看此题,就发现和原来做的很类似,而且利用sin(α+β)展开,容易找到sinβ,cosβ的关系,再结合sin2β+cos2β=1,很自然就想到消元解方程了,就是没想到计算会那么复杂.
学生乙:(头脑灵活,平时有点懒):读完题目,很快就找到了题目的突破口,联立方程求解,计算没什么意思,就不算了,主要是方法知道了就可以了.像乙这类学生平时缺少思考,学习习惯不怎么好,只会耍点小聪明.
学生丙:曾经碰到过类似题目,尝试过解方程,解起来很困难,后来听老师讲解拆角的方法,印象很深.对三角函数的求值问题,不同的类型要选择不同的方法.对于此题试过解方程,但发现计算量大,就尝试用拆角来解,没想到就很方便的解出来了.
2.2 教师的看法
听了学生的想法,笔者也对任课的部分老师做了探讨性的调查.经讨论,对学生的这种解法主要归结为两个方面:一是这类题目本身具有一定的难度,拆角是一种技巧,对学生的数学思维能力要求比较高.在学生的思想中,α+β始终是看成两个角的和,α,β才认为是一个单独的角,也就是对整体思想的理解还不够,所以学生很难想到把β看成是(α+β)-α.二是学生受到惯性思维的影响,一看到这道题目就自然而然想到解方程,这个想法是很自然的.但对于一个二元一次方程和一个二元二次方程构成的方程组,通过消元之后,虽然只有一个变量,但往往难于因式分解,要用求根公式来解,结果很多学生就被计算给卡住了.
2.3 心理学视角
这次解方程解不出来,下次碰到了大部分学生还是解方程.而且现在这一届学生如此,换了一届学生仍会出现同样的问题,这可能也有心理学上的原因吧!
在心理学上,学生的这种现象叫做思维惯性.什么是思维惯性呢?从心理学上讲:我们把这种按照积累的思维活动、经验教训和已有的思维规律,在反复使用中所形成的比较稳定的、定型化了的思维路线、方式,叫做思维惯性.简单地说:就是以前怎么做,我现在就模仿着做.
思维惯性一方面有利于学生按照一定的程序思考数学问题,比较顺利地求得一般同类数学问题的答案.另一方面这种习惯思维又会带来负面效应.学生由于受思维习惯的影响,不注重变换思维的方式,缺乏探索解决问题的途径和方法,缺少了思考的空间,这对学生思维能力的培养是不利的,从而也影响到学生解题能力.
那么,作为一线教师,我们该怎么做呢?笔者通过自己的教学实践,提出了几点改善的措施.
3 .改善措施
3.1 暴露学生原有的思维框架,改善学生的思维习惯
就如本文开头讲的这道三角函数的求值问题.虽然教师在课堂上讲过拆角的方法,但是过了一段时间让学生做,还是有一大部分学生利用解方程的方法.既然这样,教师就让学生顺着他们的思路往下解,而不是马上否认此方法不行.让学生出错,摔跟头,让他们从错误中寻找原因,要让他们经历困难和挫折,才能感受深刻.
本题学生错的主要有以下一些步骤:

②联立得到的一元二次方程还要用求根公式求根,学生求根公式经常算错.(能解出一元二次方程的根的学生寥寥无几)
③即使解出来了根还得检验,可能会有增根.(做到这步的学生几乎没有)
既然解方程过程这么麻烦,那有没有其他的方法呢?这时再讲解拆角的方法,学生就有一种豁然开朗的感觉.通过两种方法的对比,让学生切身体验到第二种方法的简便和优点.成功的体验不仅限于结果,还有思考的过程,有时过程比结果更精彩.回想教师自己,可能第一次解这类题时也是用解方程的方法,通过不断地积累、思考以及认知的提高,自身的思维能力和解题能力也在逐步提升.学生正处于积累经验的初期,在解题中培养学生悟性尤为重要.我们可以以典型题为载体,让学生经历失败与成功,培养学生多尝试的思考模式和探究习惯,这是一条突破学生惯性思维的有效途径.
3.2 加强变式教学,拓展学生思维广度.
如:函数f(x)=x2+bln(x-1),其中b∈R,若f(x)在其定义域内单调递增,求b的取值范围.虽然是高三的学生了,但还是有很多学生是这样解的:
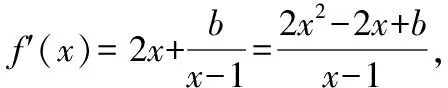
从学生的解答过程中,可以看出,学生的思维还停留在初中的水平上,对于二次函数的恒成立问题,学生习惯性的认为定义域是R,第一反应就是Δ≤0,他们的这种习惯思维导致此题失误.那么在课堂上,笔者不如这样来设计:已知函数f(x)=2x2-2x+b,
①对∀x∈R,恒有f(x)≥0,求b的取值范围.这个学生很擅长,基本没问题.
②对∀x∈[1,+∞),恒有f(x)≥0,求b的取值范围.这是二次函数定区间,定对称轴问题,但注意此时对称轴并不在定义域内,则要结合定义域求最小值.
③若f(x)=2x2+bx+2,当x∈[-1,1],f(x)≥0,求b的取值范围.二次函数定区间,不定对称轴,此时要讨论对称轴的位置.
上述设计层层递进,每做完一题,适时指出解决这类问题的要点以及前后两题之间的联系,让学生关注定义域在解决函数问题中的作用.因为很多学生对于二次函数问题,习惯的认为其定义域是R,所以要改变他们的这种习惯的思维.通过变式,加深了学生对函数概念的理解.定义域变了,即使对应法则不变,函数也是跟着变的.所以在解函数问题时首先要关注函数的定义域.通过这样的练习,他们对函数的概念有了进一步的理解,学生的思维空间得以提升,想问题,做事情也就会考虑周全,这是一种好的思维习惯.好的思维习惯的养成,对消除学生的思维惯性和培养学生的思维逻辑能力有很大的帮助.
3.3 防止解题教学的简单化
高三复习常常是以解题教学为主,因为复习的内容多,时间紧,很多老师往往分析了题目的思路,然后进行归纳,形成套路,没有分析题目所蕴含的数学思想和方法,就题论题的教学对学生的思维能力的提高是不利的.
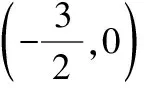
①方法上的拓展,平面几何和解析几何不是单独的两个内容,他们之间有着密不可分的联系.本题还可以利用椭圆第二定义及三角形相似这样来解:
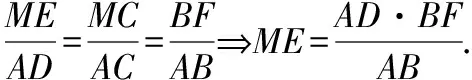

把①式代入②③中即可得ME=MF,学生惊叹,好简单呀!教师也可顺着思路讲到在历年的高考题中也经常会出现用平面几何知识来解圆锥曲线的题目.如:
( )
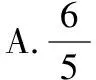
利用第二定义解比较方便.
②结论的延伸,本题的曲线是椭圆,那么换成双曲线或是抛物线是不是还有类似的结论呢?感兴趣的学生兴致就被提上来了.课后学生通过独立思考和探索,有学生说其实就是一个定值问题,等价于直线AC经过一个定点.那么,还可以进一步思考,若F点改成其他的椭圆内的与x轴的交点,定直线是准线外的其他直线,直线AC是否还经过定点呢?通过这样的变式教学,学生的思维也渐渐展开了,对题目的研究也就深了,思维的空间得到了拓展,增强了学生解题的悟性.若是碰到新题、活题,学生思考问题的空间也就不再是那么的固定和狭隘,对学生解题能力的提高是很有利的.
4.结束语


