但把试题细细看 全卷意思蔼如春
——2018年高考数学浙江卷解读与思考
浙江 杨育池
2018年是浙江省新高考改革的第二年,也是文理合卷命题的第二年.每年的6月7日下午,教师如同狂热的追剧人一样,急切地等待着数学试题“大揭秘”.帷幕拉开,可以发现2018年浙江省数学高考命题,依然坚持“起点低、坡度缓、层次多、区分好”的命题思路与风格,严格遵循国家《课程标准》、省《教学指导意见》及《考试说明》,根据文理不分科的数学素养的综合要求,聚焦学科主干内容,突出关键能力的考查,试题整体难度调控合理,“全卷意思蔼如春”,为全国新一轮数学教学改革带来积极的示范作用,对浙江省高中数学教学起到良好的导向作用.
1 注重基础,凸显人文关怀
试题在充分汲取首次命题经验的基础上,“放低起点”,符合“满足未来公民的基本数学需求”的教学理念,让基础薄弱的学生有信心动手,不至于望题兴叹,如第 11题将我国古代数学名著《张邱建算经》中的“百鸡问题”设计为解二元一次方程组,既考查考生代数变形的熟练程度和基本运算能力,也有利于考生稳定心态,纾解紧张情绪.试题也兼顾学科整体和思维价值的高度进行设计命制,“考虑差异”,对数学能力与素养的考查达到必要的深度,“满足学生对未来发展的需求”,有利于公平竞争,鼓励优秀学生独立思考,积极创新,有效地发挥并展示潜质,凸显人文关怀.
1.1 立足课本,考查基础
全卷注重数学基本概念、基础知识与基本运算的考查,绝大部分试题面向全体考生,设计取材于课本,上手易,没有偏题、难题.试题的第1~7,12~14,18题等都来源于课本,或从课本中的例、习题延伸改造而来,充分体现了数学试题的基础性.第1题考查集合的基本运算,第2题考查双曲线的简单几何性质,第4题考查复数的运算与共轭复数的定义,第5题考查函数的奇偶性及函数的零点,第6题考查空间中直线与直线以及直线与平面的位置关系,这些试题需要考生有针对性地调动数学知识进行分析运用,而不是“蚂蚁搬家”式的记忆性考核,当然不同层次的考生对知识有不同层次的理解,方法选择不当会费时低效.如果考生概念清晰,知识清楚,大可“一望而解”,无需过多动笔,给考生一种如浴春风般的愉悦轻松.
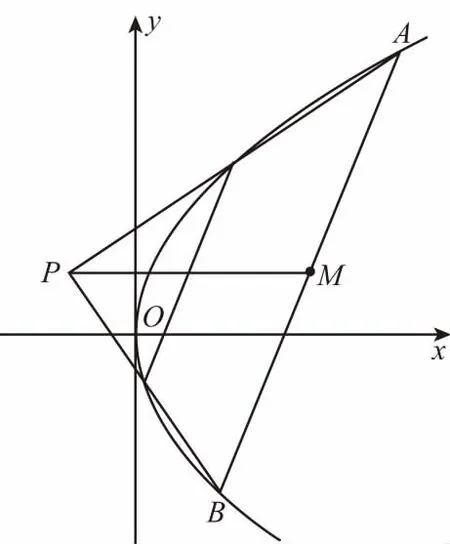
例1(2018·浙江卷·7)设0 则当p在(0,1)内增大时, ( ) A.D(ξ)减小 B.D(ξ)增大 C.D(ξ)先减小后增大 D.D(ξ)先增大后减小 对于知识面广的考生还可以利用公式D(ξ)=E(ξ2)-[E(ξ)]2简化其中的运算. 解析本题是人教A版教材必修五第一章复习参考题A组第一题的直接改编,此题不会像以往的解三角形问题边角关系隐藏繁杂,让人望而生畏,只需考生正确理解正弦定理与余弦定理,具备基本的运算技能,便可顺利解决. 又由余弦定理,有a2=b2+c2-2bccosA, 则c2-2c-3=0,又c>0,故c=3. (Ⅰ)求sin(α+π)的值; 试题聚焦高中数学的主干知识,融汇多个知识点,渗透对数学思想方法的考查,注重通性通法,关注考生在解决数学问题的过程中,所需的常用技能、思想方法和核心观念以及对数学本质的理解,有利于区分学生的数学思维能力的高低,如第8,9,17,20,21题.这些试题入口宽,往往解法多样,在解决问题的过程中,需要运用“数形结合”“设而不求”“待定系数”等思想方法.考生只有“站得高”,具备一个有组织有序的知识体系,抓住知识的本质,“才能看得远”,事半而功倍. 例4(2018·浙江卷·8)已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则 ( ) A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1 C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1 显然,两种思路均体现出在解题过程中回到定义,呈现数学概念的形成、发生和发展过程,彰显空间角问题求解的通性通法.如果更深入地揭示空间角的本质规律,则在于理解“面面角”是“线面角”中的最大角,“线面角”是“线线角”中的最小角,即可直接选择正确答案. ( ) 解析此题求解的通法是分段函数的讨论,联想到函数的本质是对应,作出函数图象,如图.则当λ=2时,函数图象位于x轴下方所对应x的取值范围为(1,4),即f(x)<0的解集为(1,4);若函数f(x)恰有2个零点,则直线x=λ左侧的抛物线部分和直线x=λ右侧的射线与x轴各只有一交点,故1<λ≤3,或直线x=λ左侧的抛物线部分与x轴有2个交点,直线x=λ右侧的射线与x轴无交点,故λ>4.综上,则λ的取值范围为(1,3]∪(4,+∞). 今年的解答题位置略有变动,数列问题难度明显下降,位置前移,在改变以往在递推关系下考不等式放缩证明,回归到等差、等比数列的条件下,研究数列的通项及前n项和等性质,贴近全省大部分高中学校的数学教学实际情况,对杜绝题海战术,重视基础,理解把握数学本质的教育观念有很好的导向作用.虽然问题设计看似很常规,但是高考是选拔性考试,所以想合理简洁得到结果,还是需要考生深刻理解数列的知识本质、并有灵活的数学思维能力和良好运算素养. 例8(2018·浙江卷·20)已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项,数列{bn}满足b1=1,数列{(bn+1-bn)an}的前n项和为2n2+n. (Ⅰ)求q的值; (Ⅱ)求数列{bn}的通项公式. 试卷立足于考查数学基础知识,突出数学本质,属于合理设置区分度较强的能力立意题,突出考查逻辑思维能力、运算求解能力和推理论证能力,体现思维的探究性,这不仅是试题设计中整合知识考查考生能力的需要,更是从不同角度有效检测考生的数学理性思维及数学学科核心素养的需要. 函数是中学数学核心内容之一,第10题是全卷的一个亮点,以数列为依托进行设计,充分体现知识和思维的探究性,需要考生挖掘“深藏”其中的函数,能引发考生对问题的“观察、猜测、抽象、概括与证明”,使之对相关数学知识进行迁移、组合并融合,发现研究对象的背景,考查考生数学抽象、数据分析和数学运算等素养,对考生的数学能力是挑战,也是对考生创新意识的淬炼.核心素养的核心是创新能力,而具有开阔的数学视野和善于发散、敢于联想的思维习惯是反映创新意识的两个重要方面.第19题侧重考查考生借助几何直观与空间想象感知空间中的直线与平面、平面与平面的位置关系,进而进行数学推理、构建数学结论,体现数学的工具性和应用的广泛性,既符合“学数学,用数学,数学就在我们身边”的现代数学理念,也能有效地从解法的创新度上投射出考生的数学素养. 例9(2018·浙江卷·10)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3).若a1>1,则 ( ) A.a1 C.a1 解析2解析1已揭示了问题的背景.解析2基于常见不等式lnx≤x-1,从整体上考虑应将“等”转化为“不等”,去掉对数符号作出推理判断.由已知得a1+a2+a3+a4=ln(a1+a2+a3)≤a1+a2+a3-1且a1+a2+a3>0,则a4≤-1.因为a1>1,故公比q<0.假设q≤-1,则a1+a2+a3=a1[1+q(1+q)]≥a1>1,即ln(a1+a2+a3)>0,而a1+a2+a3+a4=a1(1+q)(1+q2)≤0,故a1+a2+a3+a4≠ln(a1+a2+a3),所以 -1 例10(2018·浙江卷·19)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2. (Ⅰ)证明:AB1⊥平面A1B1C1; (Ⅱ)求直线AC1与平面ABB1所成的角的正弦值. 解析问题(Ⅰ)为基础知识的考查,略;下面主要考虑问题(Ⅱ),问题(Ⅱ)解法较多,可以是传统的综合法,也可以是向量法.如果把握图形的几何特征,突出转化、“割补”或“等积变换”等思想方法,则可以合理选择方法或对解法进行创新. 第21题是一道素材朴实、内蕴丰富的试题,题目本身和结论以及解法都散发着数学美的理性之光;在解法上,可以规避解析几何“程序化、套路化”的解题过程,借助数量关系上的对称性,减少运算量,彰显几何图形内在性质的雅致;在解题中,也考查考生对动点与定点,“常量”与“变量”辩证的理解,考查考生的数学建模、数学运算与逻辑推理等核心素养. 例11(2018·浙江卷·21)如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上. (Ⅰ)设AB中点为M,证明:PM垂直于y轴; 第22题以函数介值性定理为背景,不走函数问题命制的模式化的“寻常路”,紧紧围绕导数这一有力工具,研究函数的性质,需要考生综合调用导数知识、不等式等知识,还需具有通过分析观察、思考论证获取信息的能力及广阔而深刻、灵活而独到的思维品质,因而能很好地综合检测考生的数据分析、逻辑推理等数学素养及进一步学习的潜质. (Ⅰ)若f(x)在x=x1,x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8-8ln2; (Ⅱ)若a≤3-4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点. 因此,G(x)只有唯一零点.即直线y=kx+a与曲线y=f(x)有唯一公共点. 一份高考试题如果教师不能用持续的思考维持对它的热度,显然不会有“其题小而其旨极大,举类迩而见义远”的感触,也无法指导复习教学工作.反思我们的实际教学工作,每届的高考复习,我们总是希望看到自己学生的数学成绩花开月圆,师生一直在自编自导的各种“模拟”题中苦苦挣扎,以期用一张无形之网笼络住精彩的“大结局”.

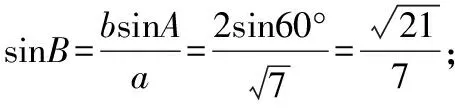

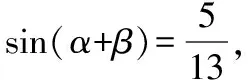
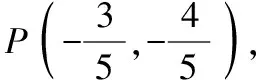
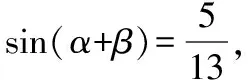
1.2 注重通法,着眼本质
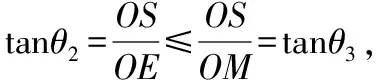

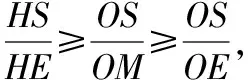







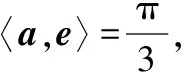



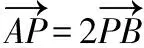


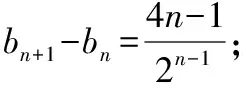
2 能力立意,聚焦数学素养
2.1 意存创新,彰显素养
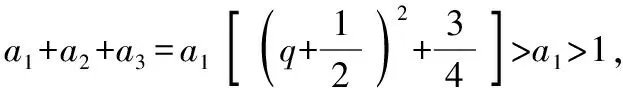

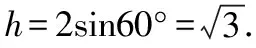
2.2 意远旨大,聚焦素养


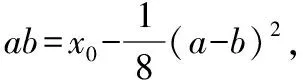

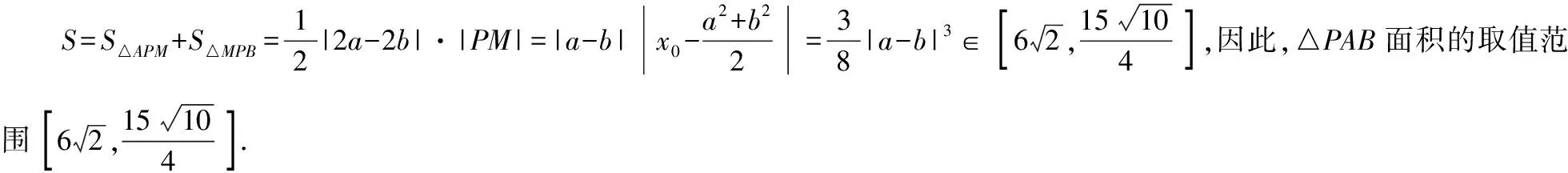

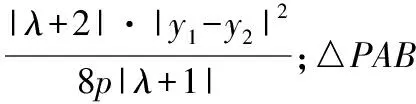
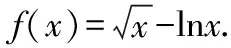

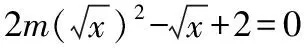
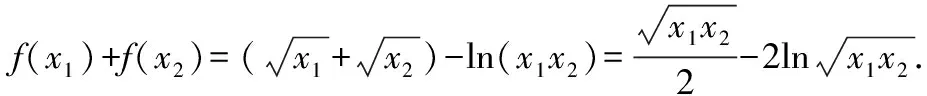
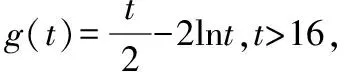
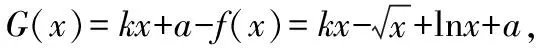
3 以思促行,启示复习教学


