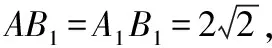立体几何一轮复习教学不容忽视的几个问题
安徽 黄海生 蒋秀梅
随着基础教育课程改革的不断深入,对学生素养的培养越来越为人们所关注.作为教师,如何将核心素养的培养真正有效地落实到课堂教学中去?学生的核心素养又如何得到体现?这都是当下关注的热点.本文结合高三立体几何一轮复习教学及笔者的一些经验和思考,提出若干个不容忽视的问题,不足之处敬请同仁批评指正.
1 不能忽视基础知识的巩固
高考复习要回顾基础知识、整理方法,但不能流于形式,合理安排时间并精读教材内容、领会教材本质,深化对教材思想方法的理解.挖掘教材例题、习题的潜力,用心体会,整合精选教材中的习题,充分发挥例题应有的功效,一题多解、一题多变、多题归一、回归本源,透过习题看数学本质.教师指导学生主动查缺补漏,构建知识网络,促进学生的反思与提升,培养学生的能力.
例1(2018·全国卷Ⅰ理·12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为
( )
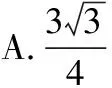


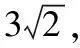
无独有偶,2013年安徽高考题也曾考查过正方体的截面问题,如下.
例2如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面积为S,则下列命题正确的是 (写出所有正确命题的编号).
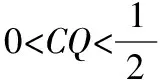
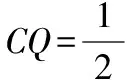


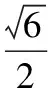
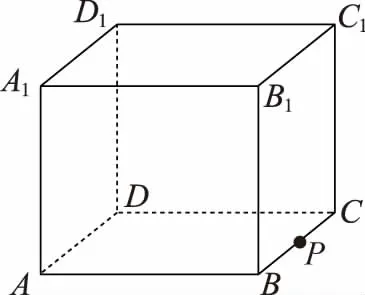
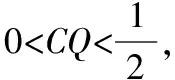
解法二:结合面面平行的性质即如果两个平行平面同时和第三个平面相交,那么它们的交线平行.过点A,P,Q的平面截该正方体所得的截面与平面ADD1A1、平面BCC1B1相交,又因为平面ADD1A1//平面BCC1B1,故交线互相平行.根据两条平行直线确定一个平面也可作出截面S.按照这种作法,当点Q在线段CC1上的不同位置时,结合平面几何的知识就可以得到相关交点,进而得到相关的截面图形.
能完整地作出截面图形是解决此题的关键.画截面与正方体有关面的交线问题,对于截面问题要利用平面的确定公理(公理2)作为理论依据,先作截面与有关棱的交点,根据“同一平面内两条直线不平行必相交”和公理1画直线进而确定交点.点动成线,线动成面,从而作出截面图形.我们可以从教材上找出这些题的“影子”.
【人教A版必修2第78页第8题】已知α,β,γ是三个平面,且α∩β=a,α∩γ=b,β∩γ=c,且a∩b=O.
求证:a,b,c三线共点.
【人教A版必修2第78页第9题】如图,平面α,β,γ两两相交,a,b,c为三条交线,且a//b,那么a与c,b与c有什么关系?为什么?

由这两个习题可知,若三个平面两两相交则它们的交线互相平行或相交.
【人教A版必修2第57页例2】已知正方体ABCD-A1B1C1D1,如图,求证:平面AB1D1//平面C1BD.

【人教A版必修2第79页B组习题2】如图,在正方体ABCD-A1B1C1D1中,求证:
(1)B1D⊥平面A1C1B;
(2)B1D与平面A1C1B的交点H是△A1C1B的重心(三角形三条中线的交点).

由这两个例题可知,若平面α与每条棱所在的直线所成的角都相等,则平面α垂直于正方体的体对角线,且根据相似三角形相关知识知道截面图形的周长均相等.
2 不能忽视作图能力的培养
理性规范的作图是解决立体几何问题的先决条件,作图就是利用图形语言描述空间位置关系.正确作图是学好立体几何的基本功,也是空间想象力的具体体现,要培养直观想象素养必须过好作图这一关,画空间图形的过程就是培养直观想象素养的过程,学生的作图水平与直观想象素养相辅相成.因此,教师不能忽视作图在立体几何教学中的地位以及在解决立体几何问题中的作用.如何正确作出图形?应重视作图的原理、规范作图.
例3如图,某空间几何体的正视图和俯视图分别是边长为2的正方形和正三角形,则该空间几何体的外接球的表面积为
( )





考试后发现很多学生不能根据三视图还原几何体,也有不少同学虽然能想象出该几何体是一个四棱锥,但是因为它的位置摆放的不“周正”,于是感觉别扭,以上原因导致解题无力为继.当几何体的摆放不“周正”时,往往难以根据三视图想象几何体的结构,我们可以考虑把几何体置于长方体(或正方体)模型中,三视图需要从后面、侧面和下面三个角度竖起与平行光线垂直的投影面,长方体(或正方体)具有现成的面可供参考.构成几何体的几何要素是点、线、面,其中点是基本元素,那么我们就把目光聚集在找出构成几何体的点上.
以棱长为2的正方体ABCD-A1B1C1D1(如图)为模型考查这个几何体.

由正视图的两条虚线可确定A1B1中点P是几何体的一个顶点,还可知C,D是几何体的顶点,结合侧视图可以排除顶点C1,D1,再由俯视图可以排除顶点A1,B1,连接相应顶点可得四棱锥P-ABCD(如图).

底面ABCD是边长为2的正方形,其中侧面PAB是边长为2的正三角形且垂直于底面,这个四棱锥的底面ABCD是面对我们的,因此很多同学不习惯,其实只要知道两个互相垂直的平面通常画成直立平面的竖边与水平平面的横边并垂直就很方便作图了,将四棱锥放置成如图所示.

3 不能忽视解题的逻辑连贯
立体几何的研究方法主要是借助于空间图形进行推理.高中教科书在内容组织上注意了以下几点:一、联系实际提出问题和引入概念,加强由实际模型到图形,再由图形到模型的基本训练,逐步培养由图形想象出空间位置关系的能力.二、从图形入手,有序地建立图形、文字、符号这三种语言的联系,在阐述定义、定理、公式等重要内容时,教科书一般是先给出图形,再用文字和符号描述对象,综合运用几种数学语言,使其优势互补,将抽象与直观结合起来,以帮助学生在图形的基础上形成更好的理解.三、加强与平面图形的联系,利用对比、引申、联想等方法,引导学生找出平面图形和立体图形的异同,以及两者之间的内在联系,逐步培养学生将立体图形问题转化为平面图形问题的能力.教师在立体几何教学中还应着重强化学生的主体地位,改变“学生被老师牵着走”的被动局面,重视过程教学,例题讲解要示范,但是不能“你画我看”“你讲我听”,更要重视学生的思维活动,“纸上得来终觉浅,绝知此事要躬行”,要让学生学会思考,透视“为什么要这样”,充分利用已有的知识切身经历并体会问题解决的过程,重视心智的参与,使学生对思想方法的来龙去脉有深切的感知.
例4(2018·浙江卷·8)已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则
( )
A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1
C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1
解析:根据异面直线所成角、线面角、二面角的定义作出θ1,θ2,θ3,再根据最小角原理即可求解;也可利用特殊值法进行求解.
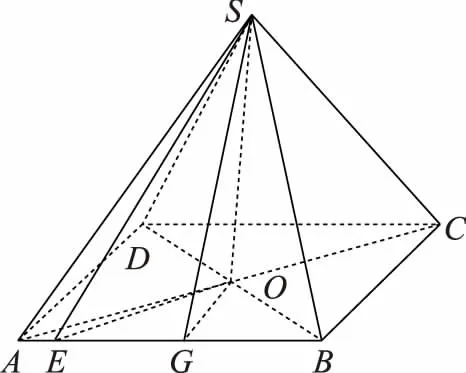
解法一:如图,连接AC交BD于点O,连接SO,则SO⊥平面ABCD,取AB的中点G,连接SG,OG,OE,则SG⊥AB,且θ2=∠SEO,θ3=∠SGO,θ3≥θ2.又θ3即为BC与平面SAB所成的角,根据最小角原理知θ3≤θ1,故θ2≤θ3≤θ1,故选D.
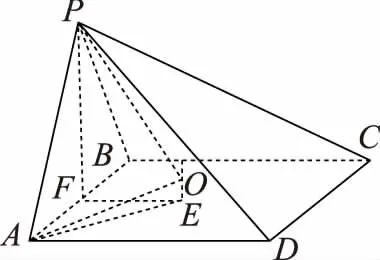
解法二:如图,设底面正方形边长为2,S到底面的距离SO=1,E是线段AB上靠近点A的四等分点,G为AB的中点,以EG,GO为邻边作矩形OO′EG,则θ1=∠SEO′,θ2=∠SEO,θ3=∠SGO,得
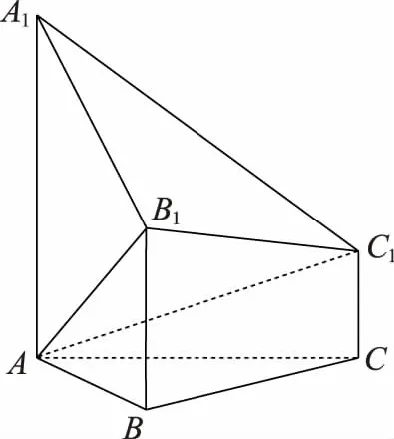
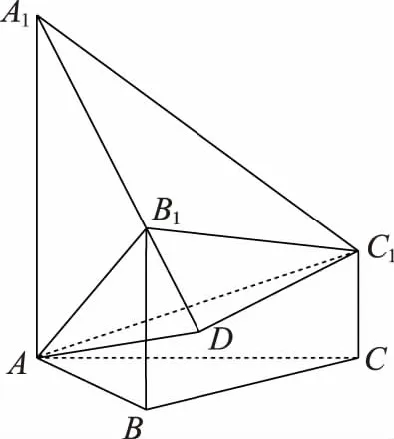
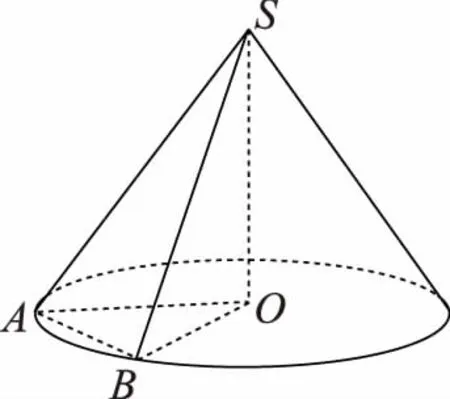
故tanθ2 当E为AB中点时,θ2=θ3=θ1. 综上有θ2≤θ3≤θ1,故选D. 本题旨在让学生体会立体几何问题“平面化”思想和“降维”思想.教学中应重视立体几何与平面知识的联系,体会转化和化归的数学思想,让学生利用类比、联想等方法理解两者的内在联系,辨别二者的区别,并感悟到将空间问题转化为平面问题是处理立体几何问题的重要思想,从而进一步拓展抽象思维和创新能力. 数学是一个整体,其整体性既体现在同一部分内容知识的前后逻辑关系上,也体现在代数、几何、三角等各部分内容之间的相互逻辑关系上.要搞好课堂教学,培养并提升学生的学科素养,不能依赖模仿、记忆,关键在于理解数学、理解教学、理解学生,善于研究教材内在的逻辑关系,站在系统的高度,整体把握教学,准确把握学生的认知基础,设计具有思考力度的问题,促进学生注重数学结构体系的系统性、逻辑性和联系性,教学中应注意各部分内容之间的联系,通过类比、联想、知识的迁移和应用等方式,使学生体会知识之间的有机联系,完善知识结构,进一步理解数学的本质,在遇到一些陌生的情境时能激活大脑中的信息,具有牵一发而动全身的效能. 本题利用三角形面积公式根据条件列出底面半径的方程,求出半径,再由条件得出圆锥母线长,最后求圆锥的侧面积. 高中立体几何课程历来以培养学生的逻辑思维能力和空间想象能力为主要目标.立体几何引入空间向量的方法后,向量作为代数与几何的载体,往往在解决立体几何二面角、夹角和距离等问题中具有明显优势,学生处理立体几何问题喜欢用空间向量的方法,久而久之,对教材中的定义、定理、性质等基础知识记忆模糊,导致推理论证能力薄弱. 例6(2018·浙江卷·19)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2. (Ⅰ)求证:AB1⊥平面A1B1C1; (Ⅱ)求直线AC1与平面ABB1所成的角的正弦值. 解法二:向量法求解(略).
4 不能忽视知识的整合构建

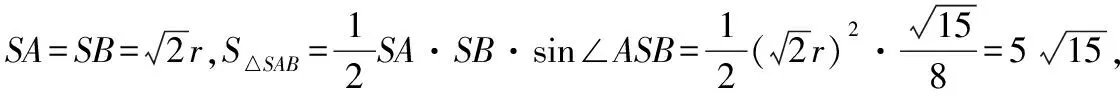
5.不能忽视论证的理性思辨