收集数据建模型 分析数据找规律——中学生养成数据分析习惯的途径

浙江 叶琪飞 余继光

大数据时代，在学会对大数据分析研究之前，即中学阶段，学会对有限的数据统计分析，特别是建立对数据的敏感性是非常有必要的，因此新课程教学目标中把“数据分析”列入学生数学学习的核心素养之一.

一、掌握数据分析的基本方法

1.数据分析是指从数据中获得有用信息，形成知识的过程.主要包括：收集数据提取信息，利用图表展示数据，构建模型分析数据，解释数据蕴含的结论.数据分析是大数据时代数学应用的主要方法，已经深入到现代社会生活和科学研究的各个方面.数据分析是现代公民应当具备的基本素质.通过数据分析核心素养的培养，学生能够养成基于数据思考问题的习惯，提升基于数据表达现实问题的能力，积累在错综复杂的情境中探索事物本质、关联和规律的经验.

2.中学生要建立数据意识，可能还需要教师的引导，特别在当前中学生只会盲目刷题、应试，不会自觉观察自然奇特现象或社会经济现象的背景下，提出有意义的问题，更加要强化，尤其在选修课程中，以小课题研究为目标，以研究性学习小组的方式，引导学生去围绕某一个问题科学地收集数据.

3.中学生要掌握数据分析方法与步骤，一方面，从调查抽样开始，掌握随机抽样的方法，科学采集数据，整理数据，分析数据，对于某个重要指标，如均值，方差，频率分布等进行分析，从而掌握社会经济统计的基本方法；另一方面，在数学解题中，面对统计与概率题目，学会从给定的数据中，按照统计整理规则，整理数据，计算特征值，分析数据，作出预测.

二、引导学生收集数据的途径

1.观察周围特别现象，用数据说话

引导学生细心观察周围社会经济现象，深入实际参与调查，善于收集数据，分析数据，指导经济活动.比如，来自绍兴农村的学生，周末回到家中从父母口中了解到，家中蔬菜大棚种植草莓在销售方面的困惑——有时不够卖，有时卖不掉，于是组织几位同学，实地调查，收集相关数据，通过分析结论，调整并指导种植方案，如下例1；

2.提出问题收集数据，用模型说话

善于从学生身边发现问题，提出问题，收集数据，建立模型，比如，从学生每天都接触的课桌椅的舒适问题入手进行的小课题研究，如下例2；

3.分析数据预测规律，用趋势说话

学生接触最多的是书本中提供的数据，或命题中提供的数据，运用正确的数据分析方法，对数据进行整理、计算、预测，用数据所呈现的趋势指导社会经济活动，如下例3、4.

三、养成数据分析习惯的体验

1.发现问题收集数据的案例

【例1】 草莓的种植与销售和地域有关，也受当时消费与供给关系的制约，因此面对草莓种植与销售问题，需要对需求量和供给量的市场进行调查，收集数据，寻找市场供求关系的平衡点，然后制定科学的种植方案，带领学生进入本地市场调查，收集数据.对草莓的市场需求量和供给量进行调查，得到以下数据：

草莓的市场需求量信息表

草莓的市场供给量信息表

根据这些信息，以供给(需求)量Q为横轴，价格P为纵轴，由已知数据在Q—P坐标系内描点，然后寻找近似的供给线和需求线，取较远的两点建立方程，求市场的供需平衡点(即需求量和供给量相等的情形).

如图，供给线近似于直线P-3Q+67=0，需求线为P+2Q-100=0(取较远的两点建立方程)，供给线与需求线的交点，就是市场供需平衡点.

由P-3Q+67=0，P+2Q-100=0，解得P=33.2，Q=33.4，即当供需量在33吨左右时，市场达到平衡，此时价格在每公斤33元左右.

为此，学生给当地草莓种植户提出建议，组织起来，成立合作社，调整种植面积，合理分配，力争保持在市场供需平衡点附近进行生产活动.

【解读】此案例具有普遍研究价值，在市场经济时代，任何商品都受着供求关系的制约，只有通过市场调查，数据分析，才能制定科学的种植方案.

2.收集数据建立数学模型的案例

【例2】 每天从早上7点至晚上9点，同学们都要生活在教室人均1平方米左右的地方，每当坐在课桌椅上听课时，有许多同学感觉不舒服，椅子太矮，腿伸不直，桌子太矮，膝关节受到压迫或磨擦，凡此种种，其原因是桌椅高度不适合自身身体，桌椅使用功能不能符合学生的实际需求.为此有必要研究适合当前中学生身体条件的课桌椅高度与功能.

首先，组织学生从两方面进行实际调查，一是学生自身身体部位的实际数据，二是测量课桌、椅子的数据(调查实际数据略).

其次，根据调查收集到的数据，建立一个课桌椅空间人体活动的数学模型，通过数学模型探索适合中学生身体特点的课桌椅空间及课桌椅尺寸，如探索小腿伸展时的轨迹，以及适合小腿伸展的桌椅高度.

如图，选择地面为x轴，椅子前面投影点为原点O，小腿与大腿连接的关节为A点，小腿AC以A为中心旋转，根据上述数据建立数学模型，探索满足下列条件的数学模型：

课桌椅空间人体活动的数学模型

(1)OA长度适合不同身高或不同小腿长的人坐；

(2)D点在旋转过程中，AD与水平面夹角为30°时应与直线EF保持一脚面距离(25cm)；

(3)人体站立时有适当的空间(30cm)，以保持人体站立时A点关节不碰撞N点桌子.

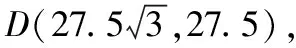
再次，为了提出适合中学生特点的课桌椅设计方案，结合数学新课程中的三视图，对已有的课桌椅进行三视图绘制，然后提出课桌椅设计修改方案，动手绘制图纸(略).

最后，结合学校实际，提出课桌椅设计修改方案与建议：在设计不同身体素质学生的课桌椅时要考虑下列因素：一是课桌椅高度可调节性；二是课桌椅功能多样性；三是课桌椅利用有效性.

3.依据数据建立模型预测的案例

【例3】 国外高速公路行车安全问题

下表是一位驾驶员手册：在干燥的混凝土路面上的停车距离

车速(英里/时)驾驶员反映距离(英尺)刹车距离(英尺)停车距离(英尺)2022224430335083404488132505513819360661982647077270369

假设观察从0秒计时，反映时间为0.75秒，这是一种乐观的假设.

A：制作一个停车距离相对汽车速度的散点图；

B：能否用一个二次函数来描述这一组数据？若能，求出一个以车速x为自变量，汽车停车距离d为因变量的二次函数.

建立数学模型：在高速公路或一般公路上开车，都会遇到上述问题，即当驾驶员发现前方道路上有障碍物时，要紧急刹车，这一过程中，由于人的反映需要时间，汽车由于惯性的作用也有一个刹车距离，这样停车距离=驾驶员反映时间内汽车所行距离+刹车距离，其中刹车距离与车速有关.

A.根据已知数据描述一个停车距离相对速度的散点图如下：

B.观察上述散点图的特征，可以用一个二次函数来描述这组数据.

设符合条件的二次函数为d=ax2+bx+c，将数据(20，44)，(40，132)，(70，369)代入可得

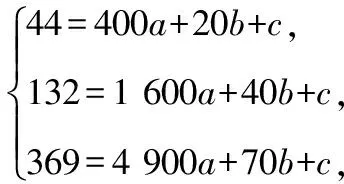
解得a=0.07，b=0.2，c=12，所以d=0.07x2+0.2x+12.

【解读】 如果选择其他数据，则所得二次函数可能不一样，其误差都比较大；如果用最小二乘法去寻找这个二次函数，其误差比较小但计算量比较大.

4.来自命题专家提供的测试案例

【例4】 (2017·全国卷Ⅲ理·18)某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完.根据往年销售经验，每天需求量与当天最高气温(单位：℃)有关.如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25)，需求量为300瓶；如果最高气温低于20，需求量为200瓶.为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574

以最高气温位于各区间的频率代替最高气温位于该区间的概率.

(Ⅰ)求六月份这种酸奶一天的需求量X(单位：瓶)的分布列；

(Ⅱ)设六月份一天销售这种酸奶的利润为Y(单位：元).当六月份这种酸奶一天的进货量n(单位：瓶)为多少时，Y的数学期望达到最大值？

【解析】 (Ⅰ)易知需求量可取200,300,500,由表格数据可知

则分布列为

X200300500P152525

(Ⅱ)①当n≤200时，Y=n(6-4)=2n，Ymax=400，此时n=200.

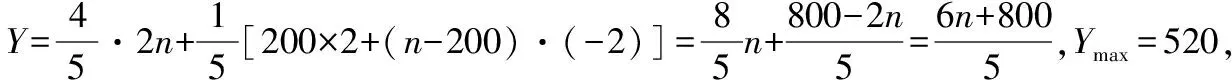
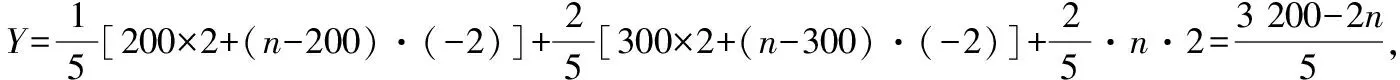
④当n≥500时，易知一定小于③的情况.

综上所述，当n=300时，取到最大值，最大值为520.

【解读】 考生面对专家提供的“频数分布表”数据，将统计数据与所求事件概率紧密相连，从而得到随机变量的概率分布，这一环节需要的是统计知识与概率知识，以及审题能力.

第(Ⅱ)问需要的是，对随机变量特征值“数学期望”概念的理解与计算方法的掌握，这一环节也是数据处理的重要一环，学生在解题训练中可以提高数据分析能力.

数据分析核心素养的培养是一个较长的过程，途径的每个方向都非常重要：

一是来自于生活实践的数学眼光，没有眼光的能力是短暂的；

二是来自于亲身体验的数学实验，没有实验的能力是空洞的；

三是来自于问题解题的数学实践，没有实践的能力是空乏的.