宝剑锋从磨砺出
——探究2018年全国卷Ⅱ文科导数题证法有感
陕西 蔡正文
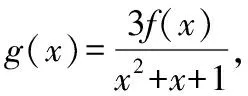
一、探究历程
(Ⅰ)若a=3,求f(x)的单调区间;
(Ⅱ)证明:f(x)只有一个零点.
【解析】(Ⅰ)略.
(Ⅱ)证明:因为f′(x)=x2-a(2x+1),①当Δ=(-2a)2-4×1×(-a)≤0,即-1≤a≤0时,f′(x)≥0恒成立(当且仅当a=0且x=0或a=-1且x=-1时,取等号),此时f(x)单调递增,所以f(x)只有一个零点;
②若a<-1或a>0时,(注:做到这里自然首先想到的是求出导函数的两个零点,然后再判断它们对应的原函数值的正负,由于导函数零点是关于a的无理式,所以“可操作性”极小,因而放弃这种想法,考虑到运用“设而不求”的策略)

②当a>0时,因为f(x)极大值=f(x1)<0,所以f(x)在(x2,+∞)有唯一零点,在(-∞,x2)无零点,即此时f(x)在(-∞,+∞)只有一个零点;
综上所述,f(x)只有一个零点.
【总评】①三次函数当x→∞时,f(x)→∞,因此要证明函数f(x)有唯一零点,只需证明函数f(x)单调或虽不单调但其极大值小于零或极小值大于零即可;②此法虽然思路清晰,但从操作层面看未必可行,即解出导函数零点代入原函数未必容易证明原函数极小值大于0或极大值小于0,尝试后果然如此!为此想到设而不求,通过整体代换变原函数极值的三次式为二次式,再通过对二次三项式的讨论得出原函数值的正负,使问题得以证明.
二、方法迁移
证完该题后,印象中以前高考真题中好像还有道可以转化为三次函数有唯一零点证明题,而且原参考答案也用了“出奇制胜”的解题招数.那么那道题能否用同样方法来证明呢?于是笔者在电脑中查到了这道题是2014年全国卷Ⅱ文科21题,并尝试着用该方法证明这道题的第二问.
【题目】已知函数f(x)=x3-3x2+ax+2,曲线y=f(x) 在点(0,2)处的切线与x轴交点的横坐标为-2.
(Ⅰ)求a;
(Ⅱ)证明:当k<1时,曲线y=f(x)与直线y=kx-2只有一个交点.
【解析】(Ⅰ)略.
(Ⅱ)证明:由(Ⅰ)知a=1,所以f(x)=x3-3x2+x+2.
设g(x)=f(x)-kx+2=x3-3x2+(1-k)x+4,那么原问题的证明就等价于函数g(x)有唯一零点的证明,因为g′(x)=3x2-6x+1-k,①当Δ=36-12(1-k)=12(2+k)≤0,即k≤-2时,g′(x)≥0恒成立(当且仅当k=-2且x=1时,取等号),此时函数g(x)只有一个零点;
②当Δ=12(2+k)>0即-2 对于思路二:可设φ(t)=-2t3+3t2+4(t≥0),则φ′(t)=-6t(t-1)>0,得0 对于2014年这道高考题的解答中,由于对零点xi采取了“精确定位”,使得两个思路都能解决,那么2018年的高考题能否也可采用消去参数a后再判断函数f(x)极值的正负呢?因此笔者又作了进一步的尝试. 综上所述,a<-1或a>0时,函数f(x)只有一个零点,所以问题得以证明. 【总评】虽然也需要对导函数的零点进行“精确定位”,但这道题定位却比2014年的题的难度要高得多!2018年这道题用降次转化为二次三项式后较容易证明,而2014年的题两种方法都需要对导函数的零点进行“精确定位”,两个途径难度相当.虽然两题目类似,但用相同方法去证明难度却又显示出一定差异,真可谓“年年岁岁题相似,岁岁年年法有别”. 作为一名数学老师,面对一道新题尤其是刚解密的高考题,应该保有较强的解题“冲动”和“欲望”,这种“冲动”和“欲望”往往能够使我们不受参考答案的束缚,有利于保持旺盛“创新力”. 虽然这种探究所得到的方法不一定是“大道通途”,但也绝不可能是“曲径通幽”,正如俗话所说“世上没有一把钥匙能开所有的锁”那样,也不存在一个方法可以解所有的数学题,这也许正是数学魅力所在.同时笔者并不太赞成动辄运用高等数学中洛必达法则、中值定理和泰勒展开式等来对高考题“牛刀小试”,不可否认大学教授在命制高考导数试题甚至是命制高考概率统计试题时具有一定的高等数学的背景,但他们在做答案时绝不考虑首先使用高等数学中定理、公式和方法去求解高考题,他们的这种“学术坚守”一直以来让笔者十分敬佩.
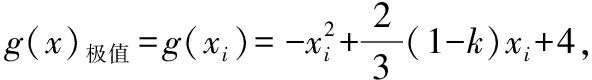



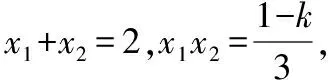
三、证后反思
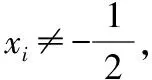



四、探究后的感悟


