关联物体问题的求解方法

孙建生

一、关联物体的速度关系

学生常对该如何分解速度搞不清楚或很难理解，其主要原因是无法弄清楚哪一个是合速度、哪一个是分速度.这里有一个简单的方法：物体的实际运动速度就是合速度，然后分析这个合速度所产生的实际效果，以确定两个分速度及分速度的方向.

例1A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体4以v1.的速度向右匀速运动，当绳被拉成与水平面夹角分别是α、β时，如图1所示.物体B的运动速度v_B为（绳始终有拉力）（    ）

例3如图6所示，一根长为/的轻杆OA，O端用铰链固定，另一端固定着一个小球A，轻杆靠在一个高为矗的物块上.若物块与地面摩擦不计，则当物块以速度v向右运动至杆与水平方向夹角为θ时，物块与轻杆的接触点为B，下列说法正确的是（    ）

二、与能量相关的关联问题

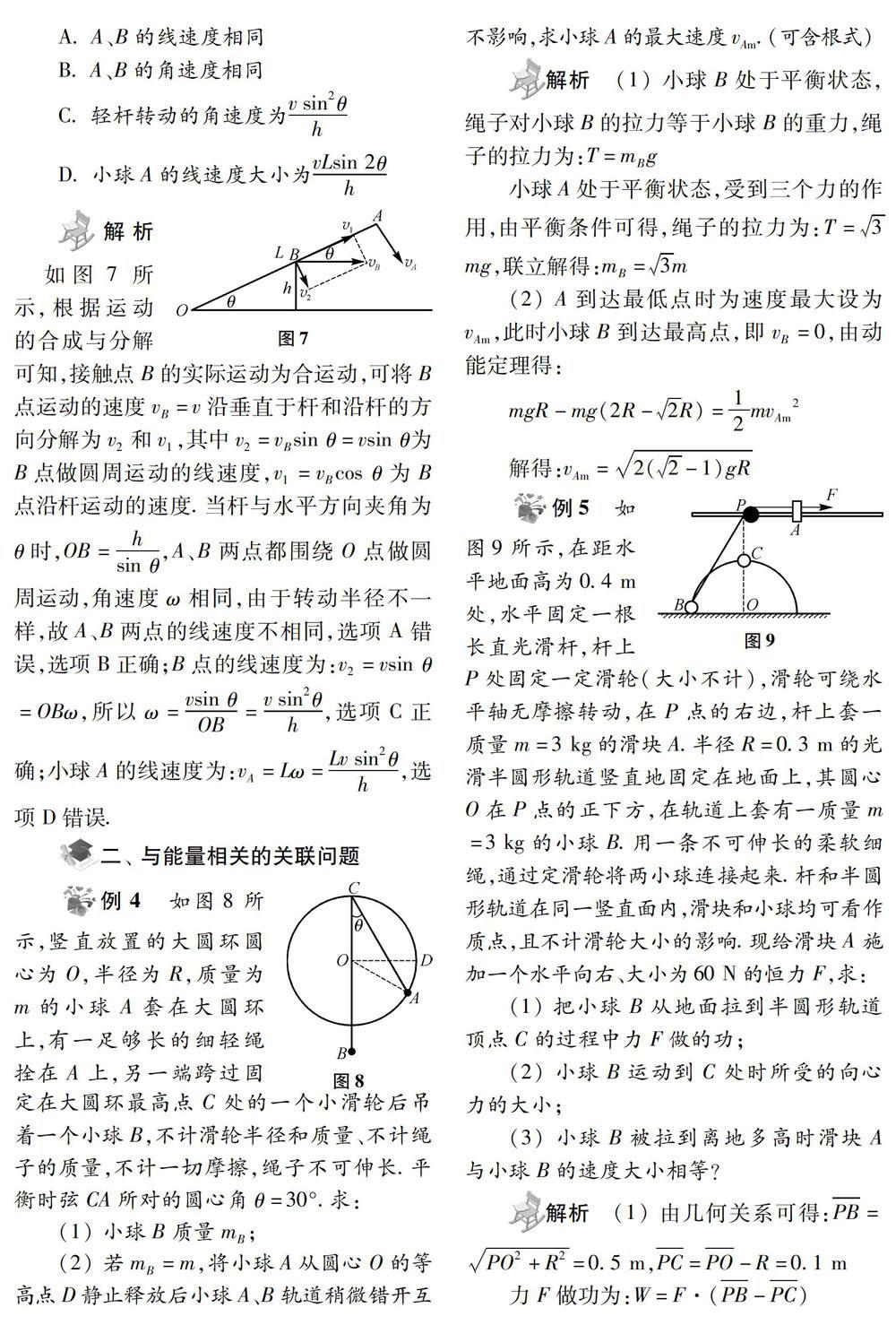
例4 如图8所示，竖直放置的大圆环圆心为O，半径为R，質量为m的小球A套在大圆环上，有一足够长的细轻绳拴在A上，另一端跨过固定在大圆环最高点C处的一个小滑轮后吊着一个小球B，不计滑轮半径和质量、不计绳子的质量，不计一切摩擦，绳子不可伸长.平衡时弦CA所对的圆心角θ=30°.求：

（1）小球B质量m_B;

（2）若m_B=m，将小球A从圆心O的等高点D静止释放后小球A、B轨道稍微错开互不影响，求小球4的最大速度V_Am.（可含根式）

解析 （1）小球B处于平衡状态，绳子对小球B的拉力等于小球B的重力，绳子的拉力为：T= m_Bg

例5如图9所示，在距水平地面高为0.4 m处，水平固定一根长直光滑杆，杆上P处固定一定滑轮（大小不计），滑轮可绕水平轴无摩擦转动，在P点的右边，杆上套一质量m =3 kg的滑块4.半径R=0.3 m的光滑半圆形轨道竖直地固定在地面上，其圆心O在P点的正下方，在轨道上套有一质量m=3 kg的小球B.用一条不可伸长的柔软细绳，通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内，滑块和小球均可看作质点，且不计滑轮大小的影响，现给滑块A施加一个水平向右、大小为60 N的恒力F，求：

（1）把小球B从地面拉到半圆形轨道顶点C的过程中力F做的功：

（2）小球B运动到C处时所受的向心力的大小：

（3）小球B被拉到离地多高时滑块A与小球B的速度大小相等？

例6 如图10所示，两根长直轨道与一半径为R的半圆形圆弧轨道相接于A、C两点，B点为轨道最低点，O为圆心，轨道各处光滑且固定在竖直平面内.质量均为m的两小环P、Q用长为√2R的轻杆连接在一起，套在轨道上，将M两环从距离地面2R处由静止释放，整个过程中轻杆和轨道始终不接触，重力加速度为g，求：

（1）当P环运动到B点时，系统减少的重力势能△E_p;

（2）当P环运动到B点时的速度v;

（3）在运动过程中，P环能达到的最大速度v_m;

（4）若将杆换成长2√2R，P环仍从原处由静止释放，经过半圆形底部再次上升后，P环能达到的最大高度H

在解决关联物体的问题时，首先要清楚物体间是通过绳、杆关联还是直接接触的，找到两物体在运动过程中速度存在的关系，分析物体实际运动的方向，然后分析这个合运动所产生的实际效果，在绳和杆不伸长的情况下，两物体沿绳或杆方向的分速度大小相同.