基于合理性问题思考的数学课堂教学设计——以“生活中的比”为例

◇傅赢芳 叶洋英

尼斯（Niss）指出，数学教师在设计教学时需要思考三个问题：一是合理性问题 （为什么要学），二是可能性问题（是否可能），三是可行性问题 （如何实施）。尽管 《义务教育数学课程标准（2011 年版）》（以下简称《课标》）和教材在编制时已经从理论上从宏观的角度充分论证了这三个问题，但是，这是否意味着数学教师在上课时就无须思考这些基本问题了呢？其实不然！事实上，教师在面对课题时，针对第一个问题，应做微观层面的思考，对其思考与否决定了课堂教学的深度与逻辑。当然，这里的合理性问题并不是指形成课堂教学目标，而是从数学或学生经验出发寻求知识之间内在的本质联系。本文以北师大版教材六年级上册“生活中的比”为例，谈一谈思考合理性问题给教学设计带来的影响。

一、合理性问题思考之前的教学设计

“生活中的比”这个课时的内容并不好上，原因是教完以后，无论是教师还是学生，都感觉自己在教或学除法。那么，这节课一般是怎么上的呢？刘琳娜老师在 《对小学教学概念教学的思考——以“比的意义”为例》[1]中展现了一些教师的做法，即直接呈现比的内容，虽然给它穿了“国旗”的外衣。北师大版教材则是以拉伸前后的一组图片（如图1）为情境，围绕两个问题——“观察上面的图片，哪几张图片与图A比较像”及“上面这些图片的长和宽有什么关系”来完成概念的引入。在解决第二个问题时，考虑两个角度，一是相像的两张图片的长之比等于宽之比，二是相像的两张图片各自的长与宽之比相等。在此背景下抽离出其中的数学式子，并将“两个数相除”定义为“比”。比如，下面这位老师的教学设计：

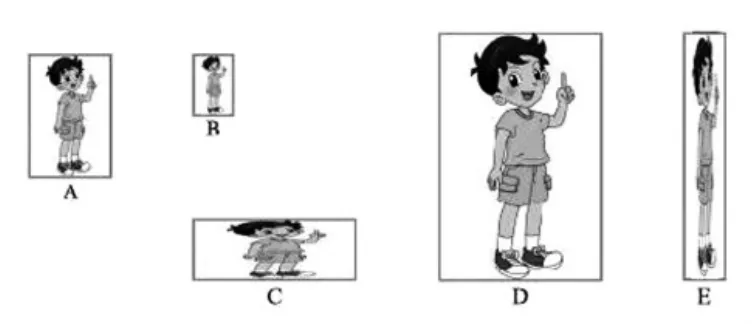
图1

师：老师带来了一组图片。（出示图1）同学们观察一下，这些图片像吗？

（1）仔细观察，哪几张图片与图A比较像？请自由说一说。

（2）大胆猜想，为什么这几张图片比较像？（出示图片 A、B、D）学生讨论。

师：你们认为这些图片像不像与什么有关系呢？

教师提示：与图片的大小、长短、宽窄有关系。

师：你们都猜想，这些图片像不像与长方形的长和宽有关系，现在我们一起验证这个猜想。算一算，想一想：这些图片的长和宽有什么关系？（课件出示带有方格的图片A、B、D）

学生尝试在练习本上用算式表示图片的长和宽的关系。比如，A：6÷4=1.5，B：3÷2=1.5，D：12÷8=1.5，或者是：宽是长的三分之二。

上述教学基本上是按照教材的情境与问题展开的。教学结束后，学生能很好地完成课后诸如求路程与时间的比、正方形周长与边长之比及其比值的问题。那么，这是否意味着学生理解了“比”的意义呢？事实上，课后对学生进行访谈时发现，学生并不能很好地明白为什么要引入“比”这个概念，尤其是之前已经学习了除法。学生会做的形式练习，实质上是套用概念，即使教师没有上这节课，没有出示图片拉伸的情境，而只是呈现“两个数相除又称为这两个数的比”这种言语形式的概念，学生也完全可以依葫芦画瓢地完成。如此看来，这节课的要点不在于会形式地写，会形式地计算，而在于理解为什么需要“比”。也就是说，如果教学伊始，教师就谨慎地思考过“为什么学习‘比’”这个问题，教学侧重点会发生变化，教学效果也会发生变化。

二、对合理性问题的深入思考

为什么要学习“比”？教师必须首先回答这个问题，然后考虑如何将自己的思考结果“展示”给学生。

为什么需要学习“比”？可以从这样几方面理解：

（1）拓宽原有对除法的理解。原有对除法的理解包括等分除 （把m个物体平均分给n个对象），以及包含除（m中含有多少个n）。但在这里，除法拓展为一种相对的比较。比如，长方形的长与宽之比是6∶4，表示长是宽的1.5倍。再如，做糖水时，糖与水之比是1∶10，表示所放的糖是水的那么，需要解决的新的问题是什么呢？既然是拓宽原有对除法的理解，为什么需要引进新的概念——比，而不是沿用原有概念及符号呢？在包含除与等分除中，我们关心的是结果，即得数是多少，但是在相对比较中，我们更关心除的过程。为了更好地区分两者，所以出现了新的概念——比，它用前项与后项忠实地记录了除的过程，或者说比较的两个对象。概言之，从意义上来说，除法所包含的意义更宽广，而比只是其中一种形式；从结果与过程来看，除法关注运算，关注运算结果，比则关注比较对象之间的差异。在这种理解中，可能出现的错误是：与作差比较混淆。比如，长方形的长与宽之比是6∶4，不能理解成长与宽相差2个单位，糖与水之比是1∶10，不能理解为糖与水相差9份。

（2）与分数的区别。分数表示部分与整体之间的关系，比则既可以表示部分与部分之间的关系，也可以体现部分与整体之间的关系。比如，图2中，黑色部分与圆的比是1∶4，也可以说成：黑色部分是圆的还存在灰色部分与黑色部分的比是1∶1，黑色部分与白色部分的比是1∶2等。除此之外，比还可以表示任意两个量之间的比较，比如，路程与时间之比，圆的面积与半径之比，这些则完全超出了分数的关系表达的范畴。

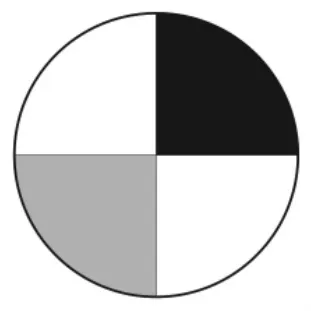
图2

此外，分数表示一个数，是一个结果形式，而比强调的是对象之间相比较的过程。

（3）实现从常量向变量的过渡。上述第一种理解确立了比这个概念的基础，那么，比在数学中起什么作用呢？比如，当给定了长方形的长与宽之比为6∶4之后，在保持比值不变的情况下，长会随着宽的变化而变化，也就产生了变量的思想。正是在这个意义下，出现了正比例函数与反比例函数，甚至后期的各种变化率。从《课标》要求及教材的后续内容看，对于比的教学，更侧重的是在控制比值不变的情况下，变化前项与后项。第一类变化是常量变化，如按比例分配问题；第二类变化是变量变化，正比例可以理解成给定比，前项（后项）随着后项（前项）的变化而变化，反比例则是正比例的横向延伸。

在各种类型的比中，又大致可以分为同一个量纲内的比较及不同量纲之间的比较。比如，长方形的长与宽之比，男生人数与女生人数之比，属于同一个量纲内的比；而路程与时间之比，总价与数量之比，圆的面积与半径之比，则是不同量纲之间的比较。如果撇开数学意义与实际意义，任何两个量之间都可以求比。

三、合理性问题思考之后的教学设计

从上面的分析看，比是出于比较的需要引入的一种特殊的量（知识点1），这种比较不是作差的形式（知识点2），而是作商的形式（知识点3），它不同于分数（知识点4），它更多地体现在控制比值不变，其中一个量随另一个量的变化而变化（知识点5）。当然，知识点5的显性化内容需要在六年级下册处理。

原有的教学设计更多地将焦点放在知识点3上，而忽略了更重要的知识点1的获得，即让学生产生学习比的需要。为此，我们重新设计这节课：依然使用图片拉伸的情境，但是在引导学生思考的方向方面做出调整。

情境描述：如图1，在一次图片制作中，A图是原图，拉伸后得到了B、C、D、E四张图片，其中B、D和A相像，C、E却变形了。那么，从数学的角度看，究竟是什么决定了图形的像或不像？（Q1）

与原来的情境创设相比，抛却了像与不像的问题的过渡，因为我们的目的是引出比的概念，所以不能把问题的焦点放在图片的像或不像上，而是需要着眼于变化过程中哪些量是不变的，哪些量是变化的。因此，问题需直指研究的核心。

为了更加自然地不露痕迹地为学生指出探究的方向，可以再提出两个辅助的子问题：Q1-1：图片是什么形状？可以从哪些量研究它？Q1-2：哪些量在A向B、D变化的过程中没有变化，但在A向C、E变化的过程中发生了变化？设立子问题Q1-1的目的是为学生的探究提供思考的方向。之前我们研究长方形时经常考虑的量有长、宽、周长、面积。设立子问题Q1-2的意图是让学生学会探究变化过程中的不变量，这正是数学最根本的研究思路。教师要允许学生逐个地考虑长、宽、周长、面积等的变化，在此基础上，引导学生或由学生独立探究基本量经过四则运算后得出的量是否在A向B、D的变化过程中保持不变，并进一步对寻求到的不变量进行命名。

因此，探究的焦点在于产生一个新的数学对象，而不只是简单地要求学生计算长除以宽的结果，并判断是否保持不变或发生变化，当然更不是解决图片到底像不像的问题。在探究结束后，教师的小结是点睛之笔：“通过讨论，我们发现了一种新的量：它表示长与宽的相对关系。那么如何来刻画它？同学们也想出了非常好的点子，采用相除的方法，也就是长除以宽，或者宽除以长。数学上，为了与我们之前所学习的除法运算区别，给这种量一种新的名称——比。”在此基础上，顺势提出前项、后项及比值的名称。

如此一来，将知识点1的教学作为重点体现在整个探究过程中，知识点2和知识点3则潜藏在学生的讨论中，知识点2和知识点4还可以通过后续练习进行进一步强化与分析。譬如，关于知识点2，可以在分析体育比赛比分的过程中强化；关于知识点4，则可以根据上面分析的比与分数的区别来突出。

因此，上每一节数学课，教师都需要从学生已有经验出发（如对于本节课，相关经验有：刻画长方形的量有长、宽、周长、面积，已学除法与分数），认真而又严谨地思考“我为什么需要教这个内容，学生为什么需要学习这个内容”，检视的结果会让教师对所要教的内容理解得更加透彻，从而带给学生的也会是更接近数学本质的、更富有数学味道的思考。