广义c-K估计优良性及其应用

钱 峰，张一枝

（1.常州工学院 数理与化工学院，江苏 常州 213002；2.南通大学 理学院，江苏 南通 226007）

0 引言

出现多重共线性问题时，统计人员会利用有偏估计克服最小二乘（LS）估计缺陷[1，2]。有偏估计的构造一般基于两点考虑：其一，通过在样本相关阵的主对角线上引进岭参数以解决设计阵的病态问题，如岭估计、广义岭估计[3，4]；其二，引进随机压缩系数将估计向原点压缩以获得较小的均方误差（MSE），如Stein估计[5]。

本文将在PC准则下讨论一种新的有偏估计压缩广义岭估计相对于LS估计的优良性问题；给出各待定系数的确定方法，并通过实例验证了该估计的可行性和优良性。

1 广义c-K估计

考虑Gauss-Markov模型：

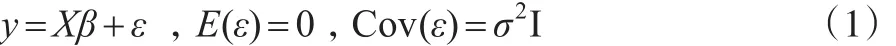
此处y是n×1维观察向量，X是n×p维列满秩矩阵(rank(X)=p)，ε是n×1维随机误差向量，β=(β1，β2，…，βp)′是p×1维未知参数向量。

对于p×p的正定矩阵X'X，必存在正交矩阵Q，使得：

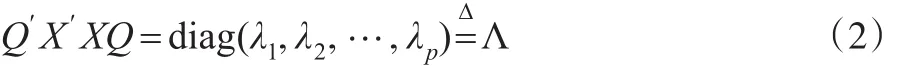
其中，λ1≥λ2≥...≥λp＞0为矩阵X'X的特征值。

对于模型（1），=(X′X)-1X'Y可作为未知参数β的LS估计。且有

设计矩阵矩阵X'X几乎奇异或病态时，

定义1[2]：模型（1），β的岭估计(ridge estimator)为：

其中k≥0为岭参数。

定义2[3]：模型（1），β的广义岭估计(general ridge estimator)为：

其中K=diag(k1，k2，...，kp) (k1，k2，...，kp≥0) 称为广义岭参数。

定义3[5]：模型（1），β的Stein估计(stein estimator)为：

其中，0≤c≤1为Stein压缩系数。

近期，统计工作者提出了用一种新的有偏估计类广义c-K估计，在考虑压缩估计的同时通过解决设计阵存在共线性或近似共线性时的问题。

定义4[6，7]：模型（1），β的广义c-K估计为：

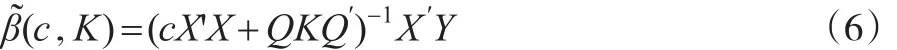
其中K=diag(k1，k2，...，kp)(k1，k2，...，kp≥0) 称为广义岭参数，参数c≥1为压缩因子。

易见，(c，K)是一个很大的估计类。特别地，c=1且K=kI(k≥0)时，得到β的岭估计(k)；K=O（零矩阵）时，得到β的Stein估计c-1)；当c=1且有KQ=QK成立时，就得到β的广义岭估计

2 PC准则下广义c-K估计估计的优良性研究

PC准则[8，9]作为比较不同估计量优劣的一个准则，原理为：设和为参数θ的两个不同估计量为损失函数，若：

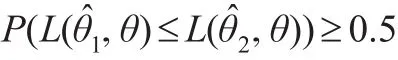
对一切θ∈Θ严格不等式“＞”至少对某θ∈Θ成立（Θ为参数空间），称在PC准则下优于。

本文将讨论对于损失函数：

在PC准则下，广义c-K估计相对于LS估计的优良性问题。

为方便起见，记A=cX′X，G=QKQ′，Γ=A-1+G-1，则易知AG=GA，则A和G可同时对角化，事实上由上文和G=QKQ′知：

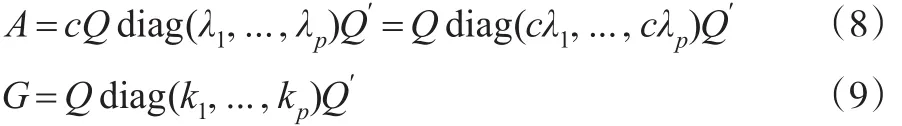
其中λ1≥λ2≥...≥λp≥0 是X'X的特征值，k1，k2，...，kp≥0是广义岭参数。

引理1：当c≥1时，cA1-A21是半正定矩阵，即

其中A1=(c-1)I+Γ-1A-1。

证明：设A1的特征值为μi(i=1，2，...，p)，下证c≥1时，对∀i有μi2≤cμi成立。

事实上，利用公式（8）和公式（9），容易计算得：

则：

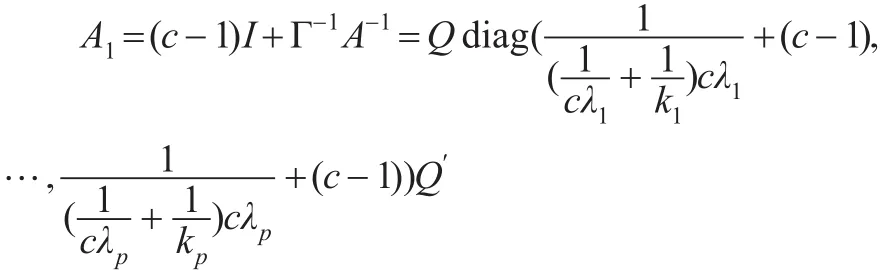
即：

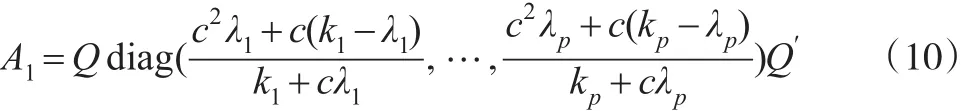
故A1的特征值分别为：

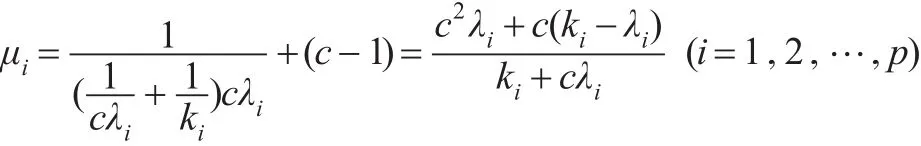
注意到：

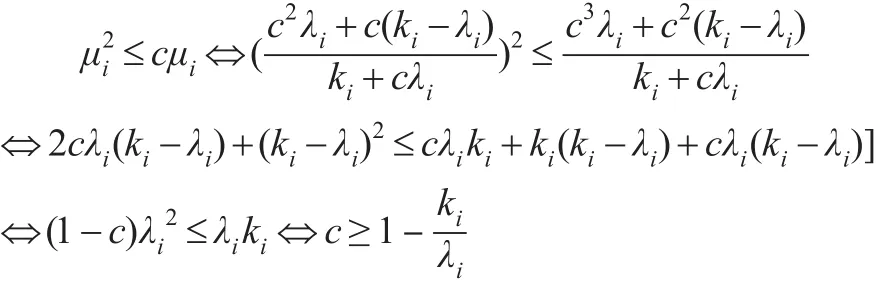
又由于c≥1，故显然成立，则(i=1，2，...，p),故引理成立。

另外，记：

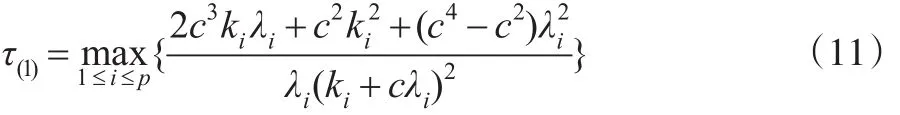
证明：

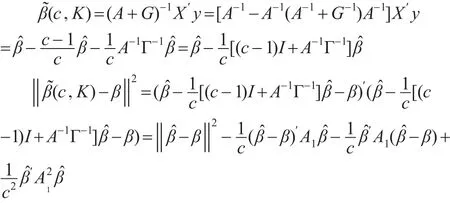
从而：

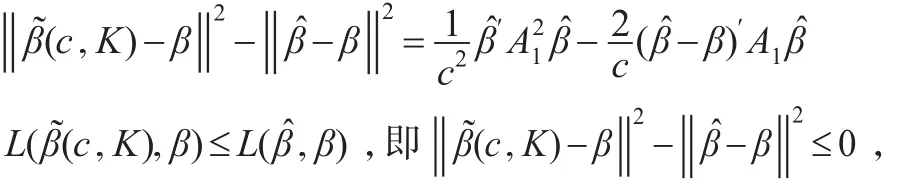
亦即等价于以下不等式成立：

而式（12）等价于下式：

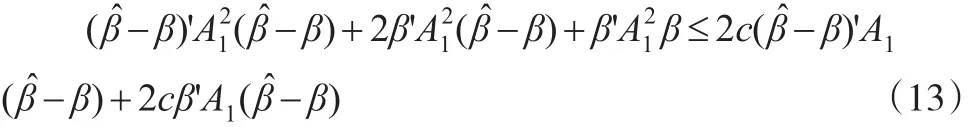
由引理知，A2

1≤cA1，故不等式（13）成立的充分条件为：

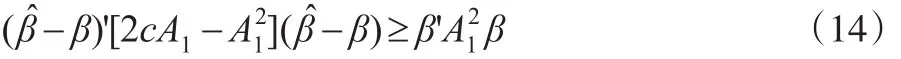
利用最小二乘估计的性质，易知-β的均值向量和协方差矩阵分别为：

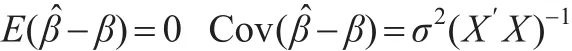
同时本文对于模型（1）作进一步假设：ε～N(0，σ2Ι)，故有：

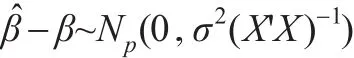
若记Z，则易知Z～N(0，Ip)。

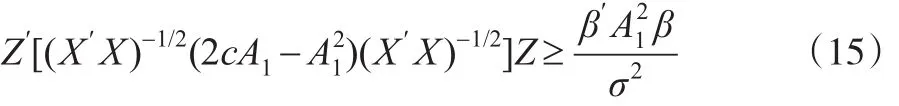
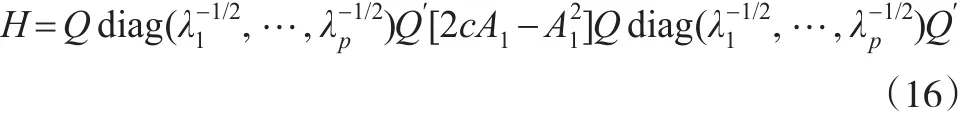
利用式（10）可求得H=Qdiag(τ1，τ2，…，τp)Q′，其中：

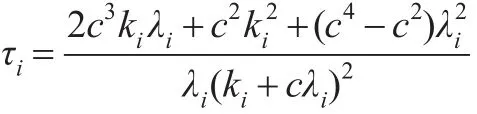
令B=Q′Z，则易知B～N(0，Ip)，故式（15）成立的充分必要条件为：

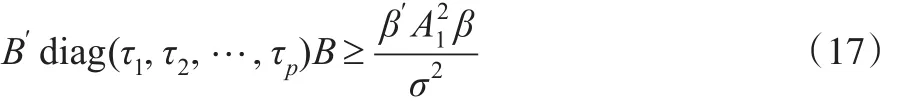
另由式（11）易知：

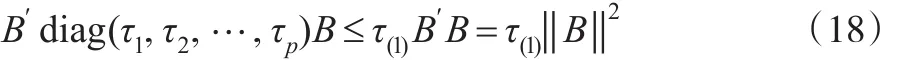
其中‖B‖2服从自由度为p的中心卡方分布。

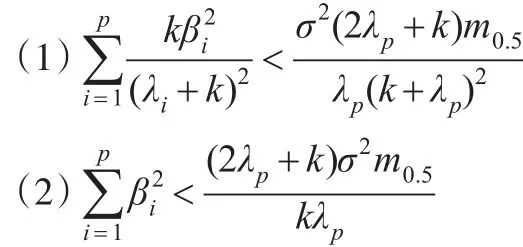
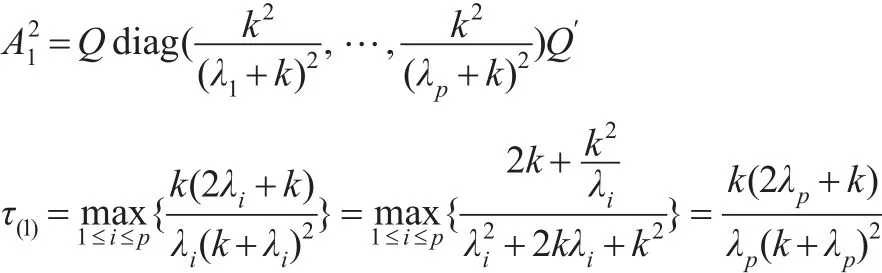
故：

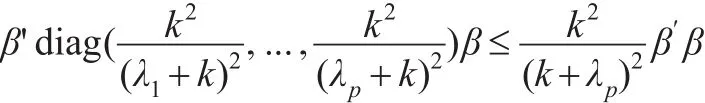
故上述推论得证。

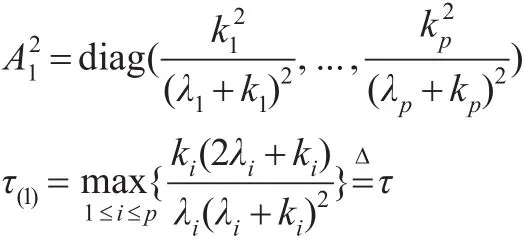
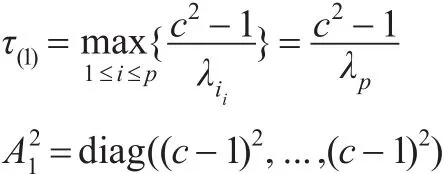
3 实例

3.1 广义c-K估计参数c和K的确定准则

根据式（7）已经推导出有：

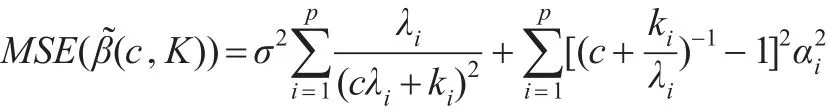
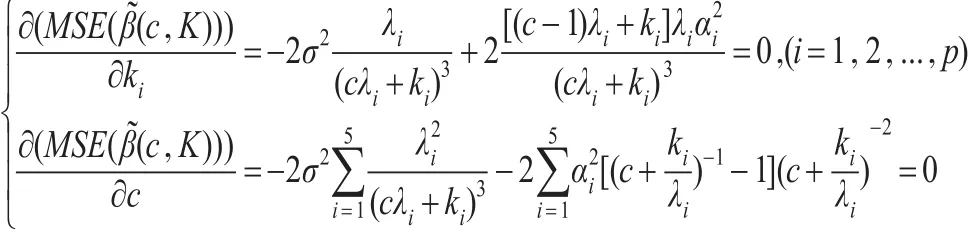
从中求的的驻点表达式为：

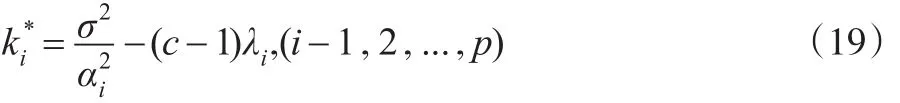
在实际问题中，由于上述表达式中σ的未知性，用数据的样本方差来代替：

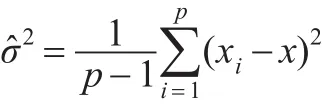
而真实值β也不易取得，故不妨用系数的最小二乘估计来代替。另外，在实际应用中未必一定要找出最优的k值,而是在均方误差准则下找到优于约束最小二乘估计的尽可能小的k值即可。

3.2 实例分析

表1（见下页）为1994—2003年共10年份的统计数据。其中Y表示民航客运量（万人），X1表示国民收入（亿元），X2表示消费额（亿元），X3表示铁路客运量，X4表示民航航线里程（万公里），X5表示来华旅游入境人数（万人）。（数据来源：《中国统计年鉴》）。

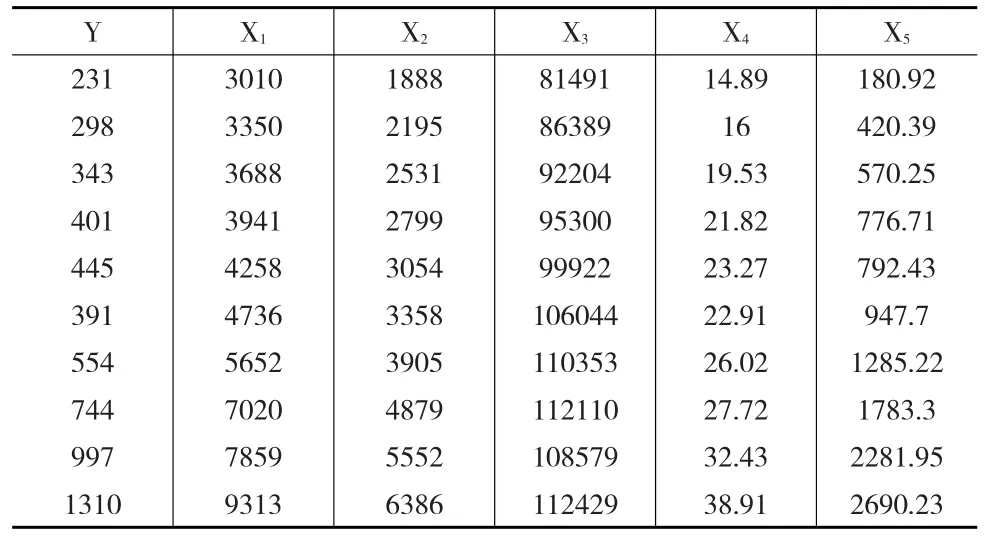
表1 中国民航客运量及相关数据

将数据中心化消除截距项后，利用最小二乘法，可得回归模型：

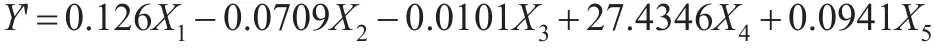
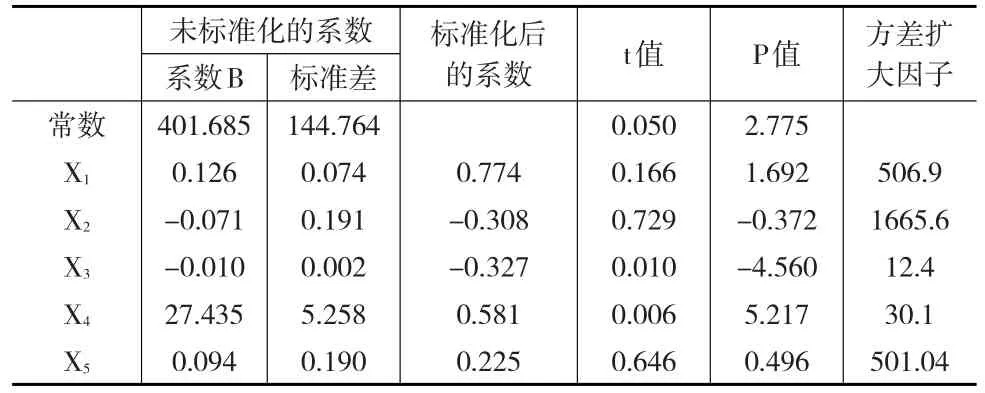
表2 回归系数表

表2表明，X1，X3，X4这三个因素对民航客运量的影响是不显著的，同时由表中的方差扩大因子都大于10，说明自变量之间存在着严重的多重共线性情况。因此，最小二乘估计不再是理想的估计。可以计算得到：

根据式（19）可以求得未知参数的表达式如下：

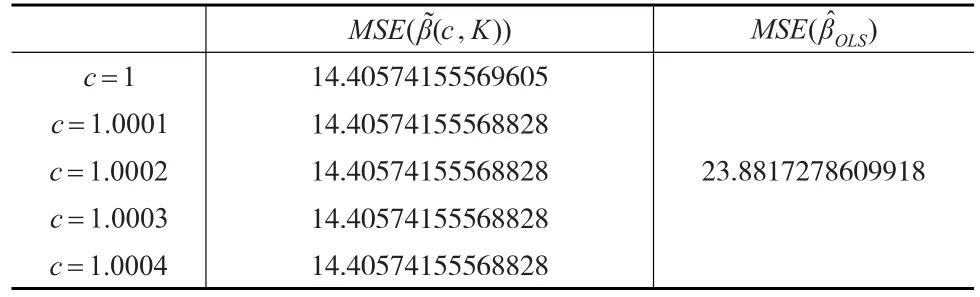
表3 两种估计的MSE值比较

另外利用式（20），确定k1=1.3644，k2=47.826，k3=3.826，k4=1.6759，k5=12.345。

4 结论

作为广义岭估计的推广估计，广义c-K估计综合体现了岭估计、Stein估计的压缩思想。通过理论证明和实例检验，均可看出其在Pitman Closeness准则、均方误差准则下均有优于最小二乘估计的良好性质。这表明：在共线性场合出现时，该估计能较好地替代最小二乘估计。