桥上半封闭式声屏障在轮轨动力作用下的振动分析
罗云柯, 张 迅, 李小珍, 阮灵辉
(西南交通大学 桥梁工程系,成都 610031)
随着我国高速铁路运营里程和运营时间的增长,一些工程问题逐渐暴露出来,如振动和噪声问题日益引起人们的关注。通常认为,当列车速度低于300 km/h时,轮轨噪声在总噪声中占主导地位[1]。声屏障是降低轮轨噪声的主要措施之一,因此,我国高速铁路多采用声屏障来降噪。
相关学者就声屏障声学性能在理论模型、预测方法和优化技术等方面均取得了不少研究成果。例如:苏卫青等[2]提出了基于双声源作为等效声源和以1 250 Hz作为等效频率的高速铁路声屏障声学计算模型;费广海等[3-4]针对我国高速铁路直立式声屏障,采用数值模拟研究了声屏障高度对其降噪效果的影响,得出了路基区段和桥梁区段声屏障的合适高度。此外,我国还开展了高速铁路鼻型声屏障、减载式声屏障等新型声屏障的研发[5-6]。
近年来,相关研究者开始关注列车脉动风对声屏障的作用。龙丽平等[7]基于流体计算软件CFX探究了列车经过声屏障时的空气脉动力分布规律。刘海涛[8]从保障声屏障结构安全工作的角度,研究了声屏障与基础连接构造的锚固性能。韩珈琪等[9]利用Fluent软件模拟作用在声屏障上的脉动风压特性,并建立有限元模型研究声屏障的脉动激励响应。张亮等[10]利用Fluent软件模拟列车以不同速度经过声屏障时的脉动力,并建立有限元模型探究了直立式声屏障的动力响应。罗文俊等[11]考虑脉动风荷载的影响,研究得出金属插板式声屏障立柱的合适间距为1.6~2.0 m。Carassale等[12]针对轨道旁的钢框架结构,实测了车致地震动和脉动风压引起的动力响应,并提出了预测模型。Tokunaga等[13]从避免共振的角度,研究了高耸直立式声屏障在列车脉动风压作用下的动力响应。
对于路基区段声屏障,其振动来源主要是列车脉动风。对于桥上高耸的半封闭式声屏障结构(如图1),其基础通常安装于箱梁的翼缘板外边缘,导致高速列车的轮轨动力作用效应不容忽视。也就是说,脉动风和轮轨激励均会引起声屏障振动;但是,二者又存在显著差异,即列车脉动风荷载是一种低频荷载,能量集中于频率几个Hz以下[10-13],而轮轨动力荷载处于中高频范围(数十至上千Hz)[14-15]。在轮轨力所引起的声屏障振动研究方面,王少林[16]基于车辆-轨道-桥梁动态相互作用原理,研究了列车过桥时的安全性与舒适性指标;蔡理平[17]等研究了全封闭声屏障在CRH2型动车组、C80型货车轮轨动荷载作用下的振动响应。

图1 高速铁路桥上半封闭式声屏障Fig.1 A semi-closed sound barrier on high-speed railway bridges
图1所示的半封闭式声屏障结构由垂直构件、水平构件、纵向连接系和单元板组成,其中,声屏障的垂直构件(立柱)和水平构件(横梁)形成主体刚架。在轮轨动力作用下,振动能量通过钢轨、轨道板、底座板、箱梁顶板和翼缘板传递到声屏障主体刚架中。为了研究这类声屏障在轮轨力激励下的中高频振动响应,本文首先采用现场试验手段对轨道结构、箱梁和声屏障主体刚架的振动进行测试,分别在时域和频域内对振动信号进行分析。然后,建立车-线-桥-声屏障耦合振动分析模型,并基于现场实测数据进行模型验证。最后,采用校验后的模型进行声屏障振动传递特性分析,并就可行的减振措施进行探讨。本文的研究成果可为今后半封闭式声屏障的减振降噪优化设计提供参考。
1 试验概况
现场试验以图1所示的桥上半封闭式声屏障为工程背景。该区段为多跨32 m混凝土简支箱梁组成的高架桥,长约1.5 km。
混凝土简支箱梁为标准设计(图号:通桥(2008)2322A-II),梁宽12.0 m,梁高3.09 m,梁长32.6 m,计算跨度31.5 m。箱梁顶板厚0.34 m,底板厚0.28 m,腹板厚0.45 m。设计速度为350 km/h,设计荷载为ZK活载,线间距为5.0 m,二期恒载取180 kN/m。
桥上采用CRTS-II型板式无砟轨道,由钢轨、扣件、轨道板、CA砂浆层、底座板、滑动层、高强度挤塑板、侧向挡块等部分组成。台后设置摩擦板、端刺及过渡板。轨道板长6 450 mm、宽2 550 mm、厚200 mm,混凝土强度等级为C60。CA砂浆层宽2 550 mm、厚30 mm,采用水泥乳化沥青砂浆。底座板宽2 950 mm、厚190 mm,混凝土强度等级为C30。扣件竖向刚度为50 kN/mm。
声屏障全高8.15 m,全宽11.7 m,立柱间距为2 m。单元板采用铝合金复合吸声板,沿高度方向共布置有13块单元板,其中,第5、6块单元板之间设有1.1 m高的通透隔声板,如图2(b)所示。声屏障刚架的垂直构件(立柱)和水平构件(横梁)为H型钢,尺寸为300×300×10×15 mm。单元板厚度为140 mm,单元板与H型钢立柱之间及上、下单元板之间垫三元乙丙橡胶。通透单元板厚度为20 mm。
图2(a)~(b)分别给出了轨道结构、箱梁和声屏障立柱上的振动传感器布置示意图。所有测点布置在跨中横断面。采用CA-YD-188型压电加速度传感器进行振动加速度测量,采样频率10 kHz。
在图2(a)中,测点V1布置在相邻两个扣件之间的中部,测试钢轨轨底的垂向振动加速度;测点V2布置在轨道板的中部;测点V3布置在底座板边缘;V4布置在箱梁顶板中心。
声屏障立柱振动测点布置在敞开侧,如图2(b)所示。其中,V5、V6和V7分别布置在与第13、10和7号单元板等高处(起算位置为声屏障底部),至立柱底部的高度分别为7.3 m、5.8 m和4.45 m。
现场测试针对过路高速列车进行,车型为CRH380B。列车通过此处的车速比较稳定,平均车速约为280 km/h。为确保测试结果的可靠性,现场监测了多组数据样本,以敞开侧行车时的测试数据进行分析。试验数据处理前,先进行初步分析以剔除异常数据,再对剩余的多组有效数据进行统计分析。
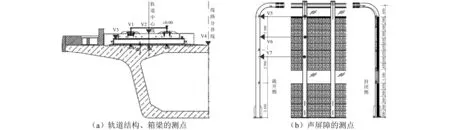
图2 振动传感器布置Fig.2 Arrangement of vibration sensors
2 测试结果分析
2.1 轨道结构和箱梁的振动
首先进行时域分析。图3给出了轨道结构和箱梁的振动加速度时程。各测点的振动加速度时程反映出背景振动要远小于高速列车强迫振动响应。
从钢轨的振动加速度时程中可以清晰地辨认出高速列车的周期性加载现象。列车通过测试断面的持时与列车整体车长及车速有关(等于车长/车速),实测加速度时程响应的持时与计算持时比较吻合(约2.5 s)。
从量值上看,钢轨(V1)的振动加速度有效值为165.08 m/s2,瞬时峰值可达4 000 m/s2;经过扣件的减振效应后,轨道板(V2)的振动加速度有效值为5.68 m/s2,瞬时峰值为50 m/s2;再经过CA砂浆和底座板的振动能量衰减后,箱梁顶板(V4)的振动加速度有效值降为1.01 m/s2,瞬时峰值为6 m/s2。上述4个测点振动加速度量值的变化反映了轮轨振动能量在轨道结构和箱梁中的传递规律。

图3 轨道结构、箱梁的实测振动加速度时程Fig.3 Measured acceleration histories of the track and box-girder
接下来进行频域分析。选取列车通过测试断面时间内的振动信号进行处理。由于轮轨激励力的频率范围很宽,本文对振动响应进行1/3倍频程分析,采用振动加速度级衡量各测点的振动强弱,定义如下[18],
VAL=201g(arms/aref)
(1)
式中:VAL为振动加速度级(Vibration Acceleration Level);arms为振动加速度有效值(m/s2),按式(2)计算;aref为基准加速度,aref=10-6m/s2。
(2)
式中:T为分析时间;a(t)为加速度时程。
图4给出了测点V1~V4的振动加速度级频谱曲线。由于钢轨测点(V1)的振动响应显著大于其它3个测点,故图4中使用了双纵坐标显示。
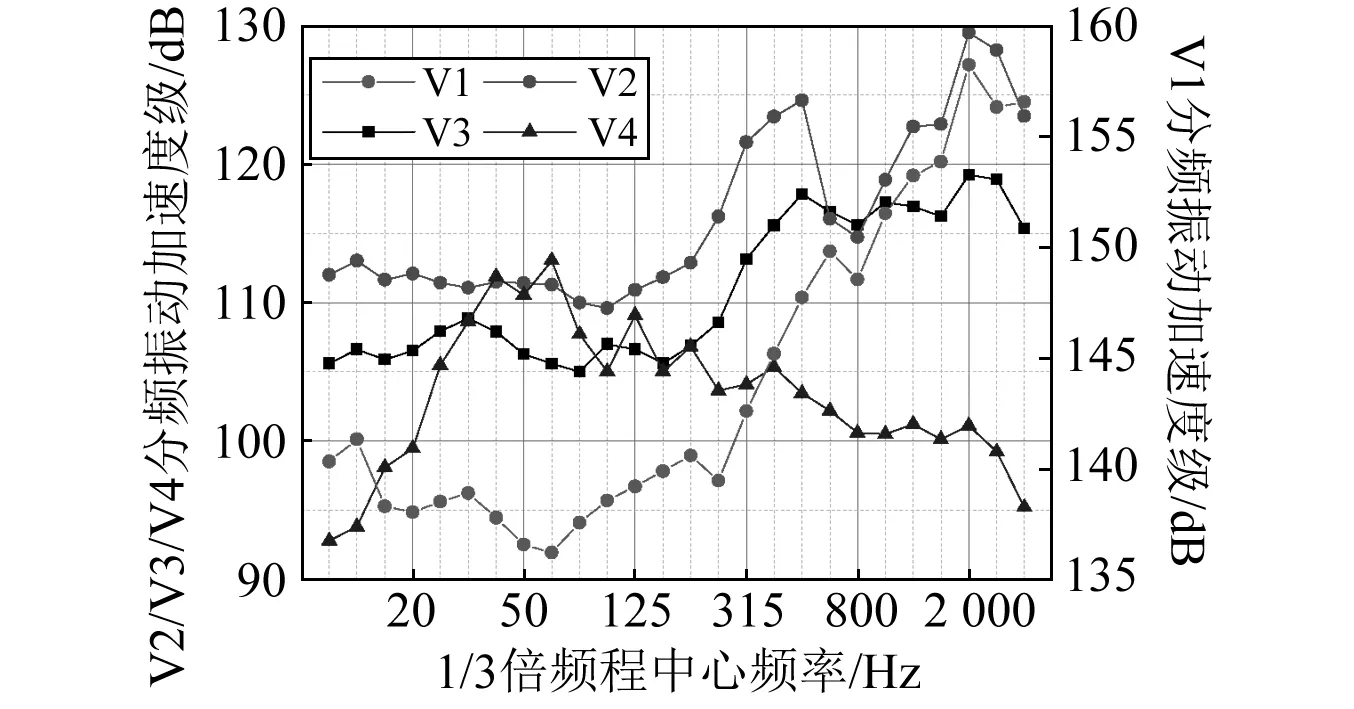
图4 轨道结构、箱梁的实测振动加速度级频谱图Fig.4 Measured VAL spectra of the track and box-girder
分析图4可以得出如下结论:
(1)总体上,随着频率增加,钢轨(V1)、轨道板(V2)和底座板(V3)的振动加速度级逐渐增大。其中,轨道板的振动加速度级频谱曲线与底座板非常相似,但前者在量值上要明显大于后者,这是由于CA砂浆起到了较好的减振效果。
(2)箱梁顶板(V4)的振动加速度级主要处于小于315 Hz的频带内,优势频段范围为40~63 Hz,这与相关研究的结论一致[19-20]。
(3)对分频振动加速度级进行叠加,可得到钢轨、轨道板、底座板和箱梁顶板的综合振动加速度级分别为164 dB、135 dB、127 dB和120 dB,即从钢轨到轨道板、再到底座板和箱梁顶板,振动加速度级分别衰减了29 dB、8 dB和7 dB。
2.2 声屏障立柱的振动
声屏障立柱通过螺栓固定在箱梁翼缘板外边缘上。翼缘板为悬臂结构,鞭梢效应将使得翼缘板产生较大的振动,并将振动能量传递给声屏障结构。
如前所述,作用在声屏障上的脉动风荷载的能量主要集中于频率几个Hz以下。为了研究轮轨力引起的声屏障振动响应,本文对实测声屏障振动时程进行10 Hz高通滤波处理,以消除列车脉动风压对测试结果的影响。图5为声屏障立柱的横向振动加速度时程。可以看出:3个测点的振动加速度时程图非常相似,且在量值上比较接近;由于测点V7位于立柱的中部,受到上部横梁和下部柱脚的约束相对弱一些,故在高速列车通过时的振动时程曲线相比上部测点V5和V6要平稳一些;V5、V6和V7的振动加速度有效值分别为0.60 m/s2、0.64 m/s2和0.67 m/s2,瞬时峰值分别为5 m/s2、5 m/s2和4 m/s2。
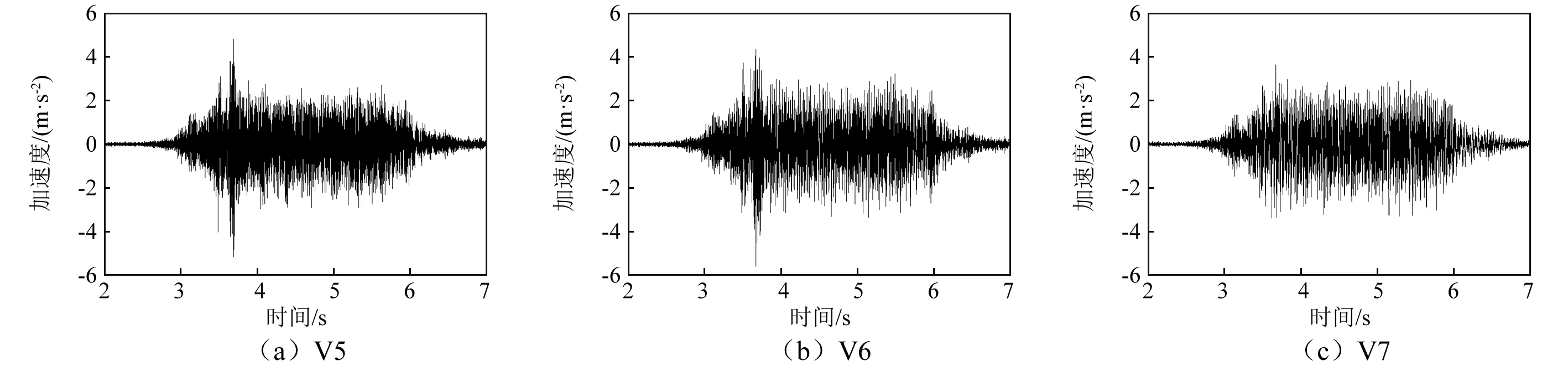
图5 声屏障的实测振动加速度时程Fig.5 Measured acceleration histories of the noise barrier
实测声屏障振动响应来源于列车脉动风和轮轨力激励,图6给出了测点V5~V7的振动加速度级频谱曲线,图中横坐标的频率范围为1~3 150 Hz。
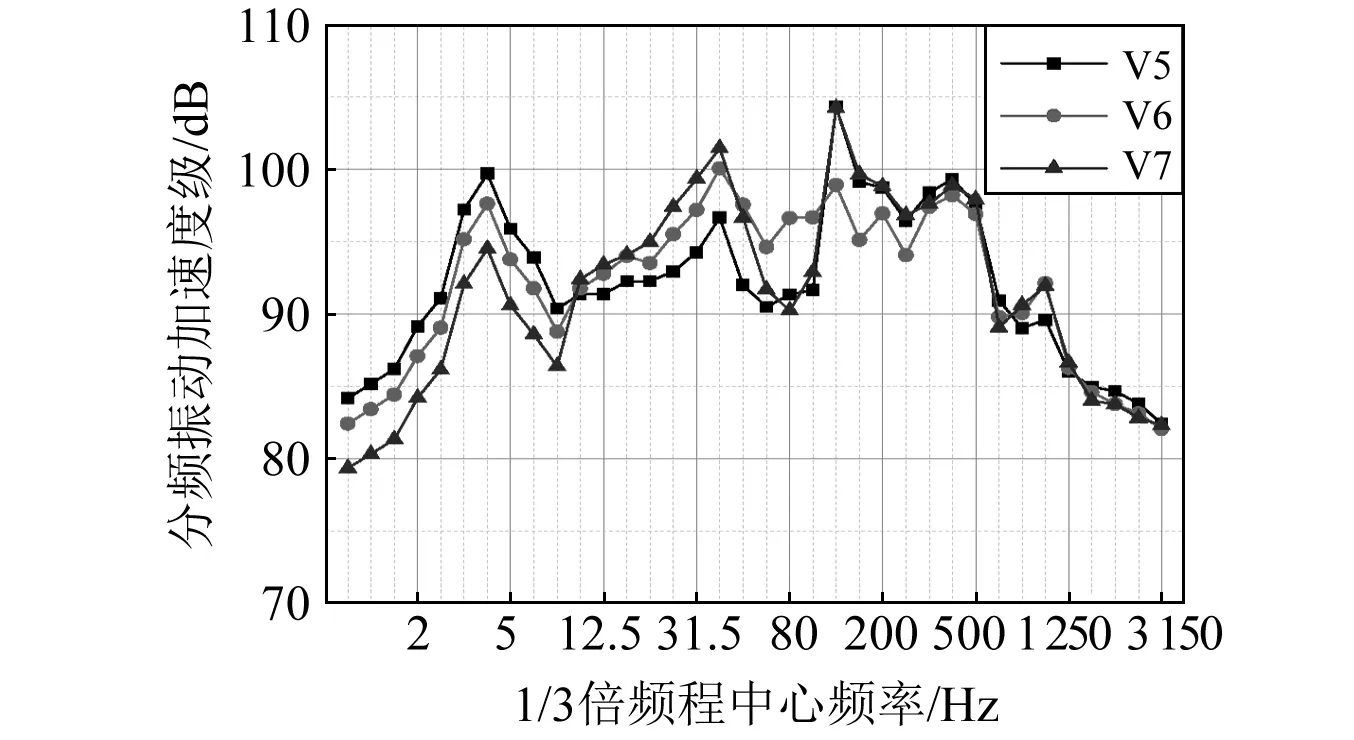
图6 声屏障的实测振动加速度级频谱图Fig.6 Measured VAL spectra of the noise barrier
从图6可以看出:在极低频段范围内(2~5 Hz),各测点振动响应出现一个局部峰值,这主要来源于列车脉动风激励;而在轮轨力激励下,3个测点的振动优势频段为20~63 Hz和100~500 Hz,峰值频率分别为40 Hz和125 Hz,这与轮轨力的频谱特性和立柱的自振特性有关。对轮轨激励优势频率范围内的振动响应进行叠加,得到3个测点的综合振动加速度级分别为109 dB、106 dB和110 dB,三者比较接近,而中部测点V7的振动略大一些。
需要指出的是:随着列车速度的提高,脉动风压将会显著增加,同时轮轨力也会不断增大。可以预见,在一定的车速范围内,列车脉动风引起的低频振动响应将超过轮轨力引起的中高频振动响应。本文仅讨论轮轨力引起的声屏障振动响应;同时,从图6可以看出,由于两种激励的频谱特性差异显著,在讨论轮轨力引起的声屏障振动响应时可忽略脉动风效应。
3 数值分析模型
3.1 箱梁-声屏障耦合振动分析模型
假设声屏障柱脚与箱梁翼缘板的连接为刚性固结,采用有限元法建立箱梁-声屏障耦合振动分析模型。在该模型中,箱梁和声屏障主体刚架均采用板单元建模,以获得结构的高频振动响应。纵向连接系采用梁单元建模,以减小模型规模、节省计算时间。
由于单元板与H型钢立柱之间垫三元乙丙橡胶,即二者之间具有足够的弹性,故忽略单元板对声屏障刚架的刚度贡献,仅将其做为附加质量考虑到声屏障刚架中。另一方面,由于高速列车脉动风荷载的频率往往只有几个Hz,故模型中忽略脉动风荷载引起的声屏障刚架振动,仅考虑轮轨动力作用效应。
图7给出了所建立的箱梁-声屏障耦合振动分析模型及典型自振模态。
由于声屏障结构的顺桥向刚度明显小于横桥向刚度,故其自振模态先表现为顺桥向振动,如图7(c)所示的一阶顺桥向振动频率为1.35 Hz。箱梁的一阶竖弯频率为4.61 Hz。

图7 箱梁-声屏障耦合振动分析模型及典型自振模态Fig.7 The box-girder-noise barrier coupled vibration model and typical natural vibration modes
3.2 车-线-桥耦合振动理论
为了分析高速列车轮轨动力作用下的声屏障振动响应,将3.1节建立的箱梁-声屏障耦合振动分析模型视为“桥梁子系统”,并基于车-线-桥耦合振动理论进行数值仿真分析。
车-线-桥耦合振动分析模型是由车辆计算模型、轨道计算模型和桥梁计算模型按一定的轮轨运动关系和线桥作用关系起来而组成的系统。运用车辆动力学、轨道动力学和桥梁结构动力学的研究方法,将车辆、轨道和桥梁看作一个耦合动力体系,分别建立桥梁、轨道和车辆的运动方程,以轮轨关系、线桥关系为联系纽带,运用数值仿真方法来求解车-线-桥系统的动力响应[14-15]。
车辆、轨道、桥梁各自由度的运动方程可运用D′Alembert原理得到,写成如下的矩阵形式:
(3)
(4)
(5)

采用分离迭代时间数值积分方法求解该动力学系统,求解列车、轨道系统动力学响应采用新型快速显式积分方法,求解桥梁结构动力响应采用Newmark-β法。更多理论推导、程序验证等详见文献[14-15],此处不再赘述。
3.3 试验验证
图8给出了声屏障振动加速度时程的仿真值与实测值对比,该时程曲线采用了10 Hz高通滤波处理。可以看出,仿真分析与现场实测的振动加速度峰值比较接近;实测振动加速度有效值为0.67 m/s2,计算振动加速度有效值为0.58 m/s2。

图8 声屏障的仿真与实测振动加速度时程对比(测点V7)Fig.8 Comparisons of simulated and measured acceleration histories of the sound barrier (measuring point V7)
图9为频域内的仿真值与实测值对比,图中分别给出了箱梁顶板(V4)和声屏障立柱(V7)的分析结果。为简便起见,图中的频段显示范围为20~1 000 Hz。不管是测点V4还是V7,仿真计算的频谱曲线与实测的频谱曲线规律一致。对于综合振动加速度级,测点V4和V7的仿真值分别为118 dB和112 dB,实测值分别为120 dB和110 dB,即仿真值与实测值的偏差较小。
从以上对比分析可以看出,在中高频范围内,可以忽略脉动风压效应,本文提出的计算方法是可行的。该模型将用于后续的声屏障振动性能和减振分析。
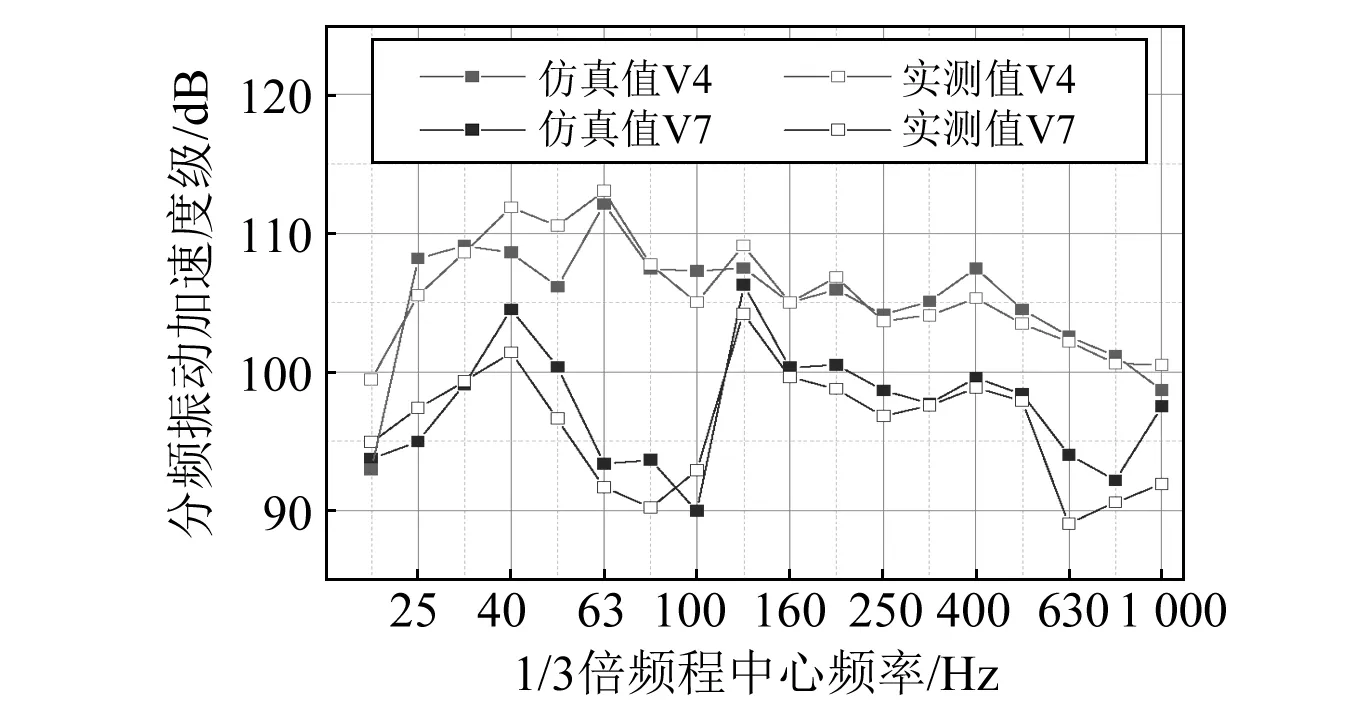
图9 频域内的仿真值与理论值对比Fig.9 Comparisons of simulated and measured results in frequency domain
3.4 车速的影响
图10给出了不同速度下,箱梁顶板(V4)和声屏障立柱(V7)的综合振动加速度级。分析可知:随着车速增加,箱梁和声屏障的综合振动加速度级均不断增加,这主要是由于轮轨荷载增加的缘故;在车速150~350 km/h范围内,考察点V4和V7的综合振动加速度级随车速提高而增加的规律分别约为5.4 dB/(50 km/h)和3.5 dB/(50 km/h),即前者受车速的影响更为明显。

图10 不同车速下的振动对比Fig.10 Comparisons of simulated vibrations at different speeds
4 讨 论
4.1 声屏障振动的分布规律
从图7(a)可以看出,该简支箱梁上共有17个声屏障主体刚架。为了分析声屏障的振动大小分布,图11(a)分别给出了跨中横截面(L/2)的声屏障刚架沿不同位置的综合振动加速度级;图11(b)给出了跨中(L/2)、四分之一跨(L/4)和八分之一跨(L/8)横截面的声屏障刚架在V7所在位置的振动加速度频谱曲线。计算车速为280 km/h。
在图11(a)中,H1~H3表示行车侧立柱的考察点,H1和H3位于两端,H2位于中部;H7~H9表示另一侧立柱的考察点,H7和H9位于两端,H8位于中部;H4~H6表示横梁的考察点,H4和H6位于两端,H5位于中部。
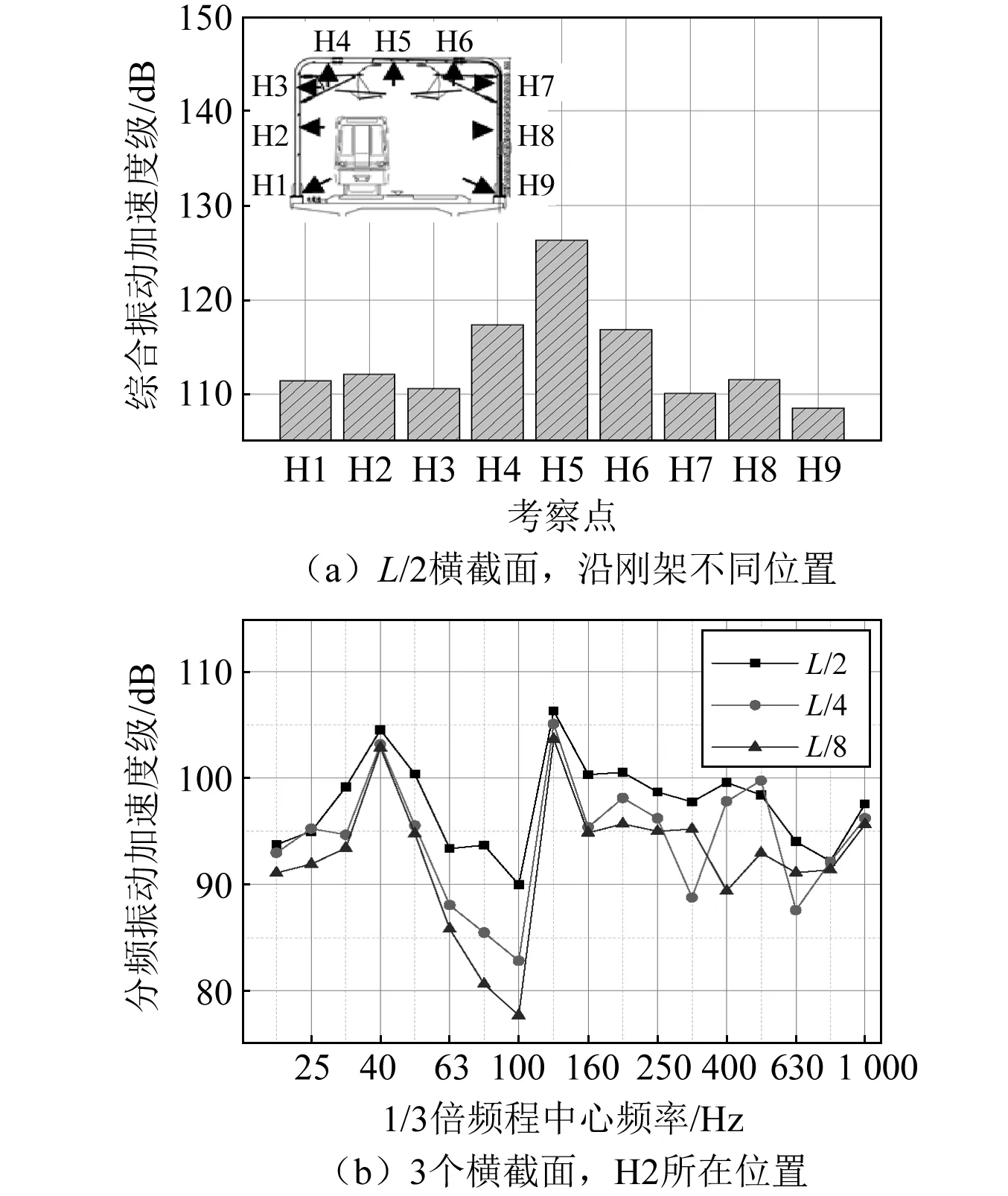
图11 声屏障各位置处的振动加速度级Fig.11 VALs of the noise barrier at different locations
分析图11可以得出如下结论:
(1)对于跨中横截面的声屏障刚架,横梁的振动要大于立柱,这是由于轮轨动力荷载以垂直方向为主。
(2)对于跨中横截面的声屏障刚架,敞开侧立柱的振动要稍大于封闭侧立柱,这是由于高速列车在敞开侧行车造成的偏载效应。
(3)对于跨中横截面的声屏障刚架,横梁和立柱的振动均表现出构件中部的振动稍大于两侧,这是由于构件中部受到两端的约束作用要弱一些的缘故。
(4)对于不同横截面的声屏障刚架,H2所在位置的分频振动加速度级的频谱曲线比较相似,只是在量值上以跨中横截面稍大,这主要与箱梁翼缘板的振动有关。L/2、L/4和L/8横截面在H2所在位置的综合振动加速度级分别为112 dB、110 dB和108 dB。
4.2 减振方案及效果分析
为降低声屏障的车致振动,本文首先讨论声屏障刚架的刚度对其振动的影响。具体分析时,提取跨中横截面的声屏障刚架的计算结果。计算车速为280 km/h。
为便于分析,以声屏障刚架材料弹性模量的变化代表刚度的变化,例如:“0.75E”表示声屏障刚架刚度折减25%;“1.25E”表示声屏障刚架刚度增加25%。图12给出了声屏障刚架刚度变化时,考察点H2、H5和H8的综合振动加速度级的变化规律。
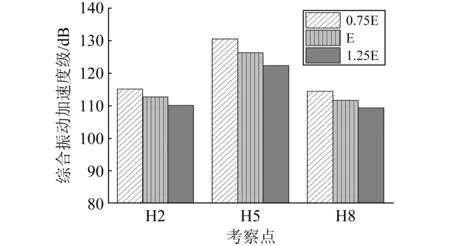
图12 刚架刚度对声屏障振动的影响Fig.12 Effects of strut stiffness on VALs of the noise barrier
从图12可以看出:
(1)总体上,随着声屏障刚架刚度的增加,其振动加速度级逐渐降低。
(2)刚度增加25%时,横梁H5的综合振动加速度级减小约4 dB;立柱H2和H8的综合振动加速度级减小约2 dB。
(3)横梁的振动受刚架刚度的变化更敏感,这主要是由于两侧立柱相当于横梁的弹性支承,横梁的振动强弱程度将受到自身的刚度大小和两端弹性支承强弱的双重影响。
前文已述及,声屏障振动的强弱程度与下部基础——箱梁翼缘板的振动大小由密切关系。考虑到箱梁翼缘板为悬臂结构,这里采用施加斜撑的方案对翼缘板加强支承。
图13给出了拟采用的斜撑方案。斜撑连接箱梁翼缘板边缘和箱梁底板边缘,采用H型钢,尺寸为300×300×10×15 mm。斜撑的间距为2 m,即与声屏障刚架等间距布置。

图13 斜撑示意图Fig.13 Diagram of the inclined bracings
图14给出了有无斜撑时考察点H2、H5和H8的综合振动加速度级对比。可以看出:无论是横梁还是立柱,施加斜撑后的振动均有明显降低,横梁和立柱的综合振动加速度级分别减小约12 dB和8 dB。显然地,施加斜撑将会增加一定的工程量,且斜撑与箱梁的连接构造需得到可靠保证,否则将会对声屏障的声学性能带来影响。

图14 斜撑对声屏障振动的影响Fig.14 Effects of inclined bracings on VALs of the noise barrier
5 结 论
(1)高速列车以速度280 km/h通过时,实测钢轨、轨道板、底座板、箱梁顶板和声屏障立柱的综合振动加速度级分别为164 dB、135 dB、127 dB、120 dB和110 dB,衰减规律与振动传递路径“钢轨→轨道板→底座板→箱梁→声屏障立柱→声屏障横梁”相符。实测声屏障立柱的振动优势频段为20~63 Hz和100~500 Hz,峰值频率分别为40 Hz和125 Hz。
(2)采用板单元模拟箱梁和声屏障刚架可以较好地反映二者的高频振动,箱梁和声屏障振动响应的仿真值与实测值吻合良好。
(3)在车速150~350 km/h范围内,箱梁顶板和声屏障立柱的综合振动加速度级随车速提高而增加的规律约为5.4 dB/(50 km/h)和3.5 dB/(50 km/h)。
(4)同一横截面上,声屏障横梁的振动要比立柱的大,且构件中部的振动要比两端稍大。跨中横截面的声屏障振动要比四分之一、八分之一横截面稍大,但三者的频谱曲线变化规律基本一致。
(5)声屏障刚架刚度增大时,其振动响应会降低。刚度增大25%时,横梁、立柱的综合振动加速度级分别减小约4 dB和2 dB。
(6)箱梁翼缘板对声屏障的振动有较大影响,对箱梁翼缘板施加斜撑可以使得横梁、立柱的综合振动加速度级分别减小约12 dB和8 dB。
展望:由于半封闭式声屏障与直立式声屏障在结构形式上差异很大,因此,列车通过时作用在二者上的脉动风压分布特征将明显不同。后续研究中,应进一步探讨半封闭式声屏障在脉动风压作用下的低频振动响应,以掌握脉动风压和轮轨动力联合作用下的全频段振动特性。

