一种EEMD-HHT与时频重排结合的转速曲线估计新方法

荣 锋， 陈 宁， 郭翠娟， 杨明珠

(1. 天津工业大学 电子与信息工程学院，天津 300387； 2. 天津市光电检测技术与系统重点实验室，天津 300387)

旋转机械广泛应用于社会生产的各个行业，保障其安全稳定的运行有着重大意义。目前，对旋转机械的状态监测与故障诊断的重要手段是对振动的监测与分析[1]。旋转机械在运行状态下的转速严格来说是波动的，尤其是升降速过程，此时的振动信号属于非平稳信号，不适合于常规的傅里叶频谱分析[2]。阶比分析是工程实际中常用的旋转机械变转速状态下振动信号的分析方法，其关键在于将时域非平稳信号通过等角度重采样转化为角度域的平稳信号，这个过程称为阶比跟踪[3-4]。阶比跟踪具体来说是指准确获得参考轴的基准频率以及得到等角度重采样时刻的过程。传统的阶比跟踪方法有硬件阶比跟踪和计算阶比跟踪，两者都需要有特定的测量转速的硬件装置，在不便安装的场合，两种方法都无能为力。近年来，随着学者不断的研究，出现了无需硬件测速装置的软件阶比跟踪技术，其关键在于从振动信号中提取出参考轴的转速曲线，从而计算得到重采样时刻。该方法极大削弱了阶比分析对硬件的依赖，得到广泛的应用。

由振动信号获取转速曲线的方法有很多种，郭瑜等首先提出利用短时傅里叶变换(STFT)或Wigner-Ville分布(WVD)的时频分析阶比跟踪方法，通过对振动信号的时频分布进行峰值搜索，从而获得参考轴的转速曲线。曹书峰等[5]提出了基于时频融合分布的转速估计方法，通过将两种时频分析的时频分布进行融合，之后再进行峰值搜索和最小二乘拟合得到参考轴的转速曲线。李辉等[6]利用Hilbert-Huang变换(HHT)获得转速曲线。以上文献虽然都有一定的成果，但是也各自存在一些问题，比如时频分析存在时频聚焦性差或交叉项干扰等问题[7]，而且在数据量较大时，产生的时频矩阵会占用极大的计算机硬件内存，大大降低计算效率；HHT变换过程中的经验模式分解(Empirical Mode Decomposition，EMD)会使相邻的本征模态函数(Intrinsic Mode Function，IMF)之间产生模态混叠，且Hilbert变换会在信号两端产生严重震荡，甚至可能出现无意义的负频率，影响转速曲线的估计精度[8-9]。

为此，本文提出一种基于EEMD的HHT与时频重排算法相结合的转速曲线估计方法。首先由EEMD得到参考转轴所对应的IMF，之后分两步得到该IMF的瞬时频率：先对IMF整体做HHT变换，得到其各个点的瞬时频率值；再截取IMF两端各一定长度的数据，分别进行时频重排变换，在得到的两个时频重排矩阵中进行限制搜索条件的瘠提取，并对瘠线拟合，得到IMF两端截取点的瞬时频率。之后用第二步得到的瞬时频率值代替第一步得到的对应点处的瞬时频率值，并由最小二乘法将“拼接”频率拟合成一条光滑的曲线，即为参考轴转频曲线，利用转频与转速间的关系即可得到转速曲线。通过对实测信号分析来详细说明算法实施步骤，分析结果表明本文方法行之有效。

1 EEMD-HHT和时频重排算法原理

1.1 EEMD-HHT算法

EEMD-HHT是对HHT的一种改进，其利用EEMD分解方法，有效的抑制了HHT变换中产生的模态混叠现象[10-11]，使得分解得到的IMF更加纯净。EEMD利用白噪声在整个频域内分布均匀的特性，在原始信号中加入白噪声，使得信号在不同尺度上连续。其在分解时要设定执行EMD的次数M，及叠加的随机白噪声序列的幅值标准差σ。EEMD-HHT的主要思想是把一个时间序列信号由EEMD分解成一系列不同尺度的单分量IMF，之后对每个IMF进行Hilbert变换，得到各IMF所对应的瞬时频率值和幅值，从而得到振幅-频率-时间的三维谱分布。EEMD-HHT有效的抑制了HHT的模态混叠现象，但是分解过程仍会产生虚假分量成分，使得有效本征模函数不好识别，而且Hilbert变换在信号端点处造成的频率震荡依旧存在。

1.2 时频重排算法

STFT变换和WVD变换是两种应用最为广泛的时频分析方法。但是前者无法兼顾时间分辨率和频率分辨率，时频聚焦性相对较差，后者分析多成分信号分量时，会产生交叉项干扰。时频重排算法最初是为了改进谱图的可读性[12]。信号x(t)的谱图定义为其STFT变化的幅值平方[13]，表达式为

(1)

式中：h(t)为STFT所用的窗函数。谱图表达式可以写成信号的WVD和分析窗的WVD的二维卷积形式

(2)

此分布一定程度上减弱了信号WVD产生的相关项，但是降低了时频分辨率，是以边缘性质和一阶矩有偏为代价的。上式表明，WVDh(t-s,f-a)是在点(t,f)附近设定了一个邻域来分配信号WVD的加权平均值。而重排算法就是将时频分布面上任意一点(t,f)处的谱值从原来位置移动到该点附近信号能量的重心

(3)

(4)

重排后谱图上任一点(t′,f′)的值是所有重排到这一点的原谱图值的和，即

(5)

式中：δ(t)为冲击函数。重排矩阵不仅利用了短时傅里叶变换的幅值信息，还利用了其相位信息，提高了时频聚焦性，改进了短时傅里叶变换所得到谱图的可读性，并且可以直接由重排谱提取瘠线，求得信号的瞬时参数。但是当数据量很大时，时频矩阵会占据大量内存空间，使得计算效率严重降低，计算时间大大增加。

2 EEMD-HHT与时频重排结合的估计方法

针对以上问题，本文提出了将EEMD-HHT与时频重排相结合的方法来估计参考轴的转速曲线，转频曲线估计算法实现的流程图如图1所示。其详细步骤如下：

(1) 将振动信号通过EEMD分解为一系列的IMF。

(2) 提取参考轴所对应的IMF分量。由于EEMD分解会产生虚假分量，因此本文提出采用相关系数与能量谱结合的方法，准确提取所需IMF。具体算法如下：首先，将所有IMF和原信号进行归一化处理，以防止对一些幅值较小的真实IMF做出误判。再分别计算各IMF分量与原振动信号间的相关系数值，相关系数公式为

(6)

式中：X和Y分别表示某个IMF分量和原始信号。相关系数越大代表该分量与原信号相关性越好，越能表示真实的信号成分，反之代表与原信号相关性不大，可能为虚假分量[14]。

图1 算法流程图Fig.1 Flow chart of algorithm

其次，定义某IMF分量中各点的平方和作为其能量的标志。分别计算各IMF的能量值，并做归一化处理，以各IMF所占的百分比作为判断指标，公式如下

(7)

式中：X表示某个IMF分量，M为IMF的个数。ek越大表示第K个IMF分量所占比重越大，越小则表示所占比重越小。由于振动信号是由参考轴转动提供动力产生的，所以其对应的IMF相关系数与能量占比两个数据都可能更大。综合考虑两种计算结果，选取相关系数值和能量占比都较大的IMF分量作为参考轴的本征模态函数。

(3) 对选择的IMF分量作Hilbert变换，得到其各个点的瞬时频率值。

(4) 截取IMF前后两端各一定长度数据做时频重排变换，得到两个时频重排矩阵。截取的数据长度可根据实际情况具体确定，本文提供如下一种方法：观察第3步得到的IMF时频曲线，将两端突变严重的数据段作为截取数据段，截取长度最好为2的N次方，以方便计算机计算，但不要过大，以免占用过多内存，影响计算效率。重排矩阵的列代表时间，行代表频率，其交叉点为该点处的能量值[15-16]。

(5) 分别对两个时频矩阵进行瘠线提取。虽然时频重排算法提高了短时傅里叶变换的聚焦性，但是由于IMF两端点处的震荡，重排矩阵中会产生明显偏离转轴频率的值。所以本文提出设置频率搜索范围进行瘠线提取，具体步骤为：

首先，设定能量阈值Ea，式中Esum为重排矩阵的总能量，N为IMF的长度。

(8)

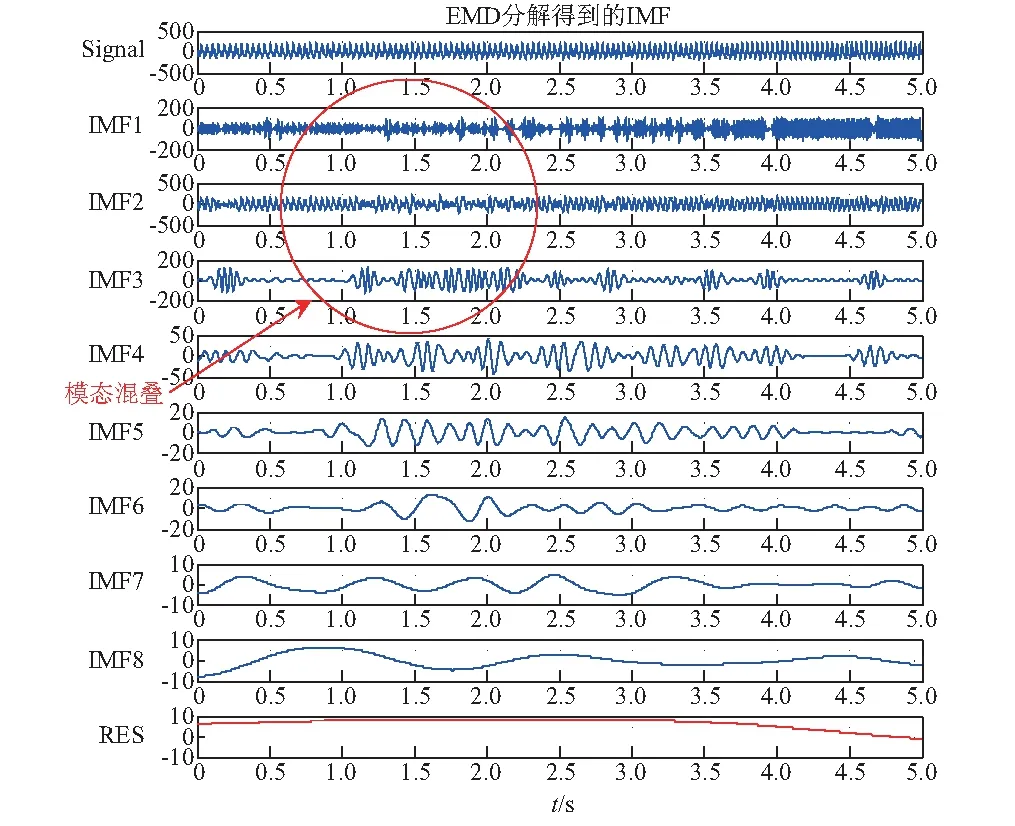
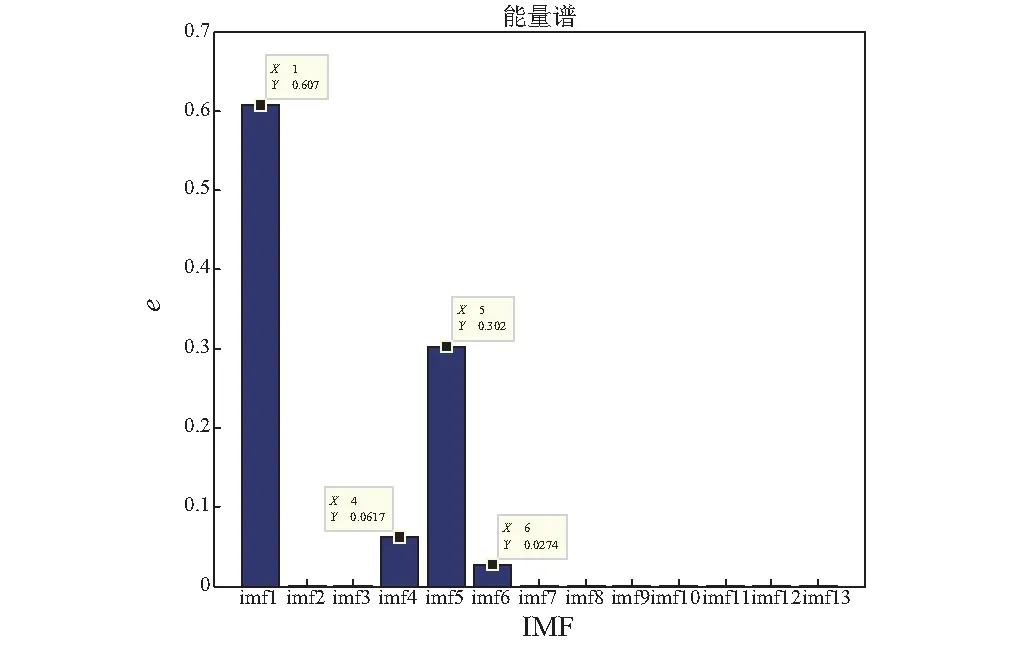
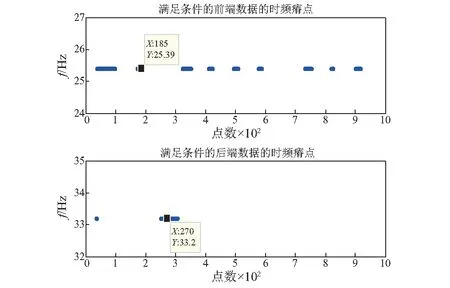
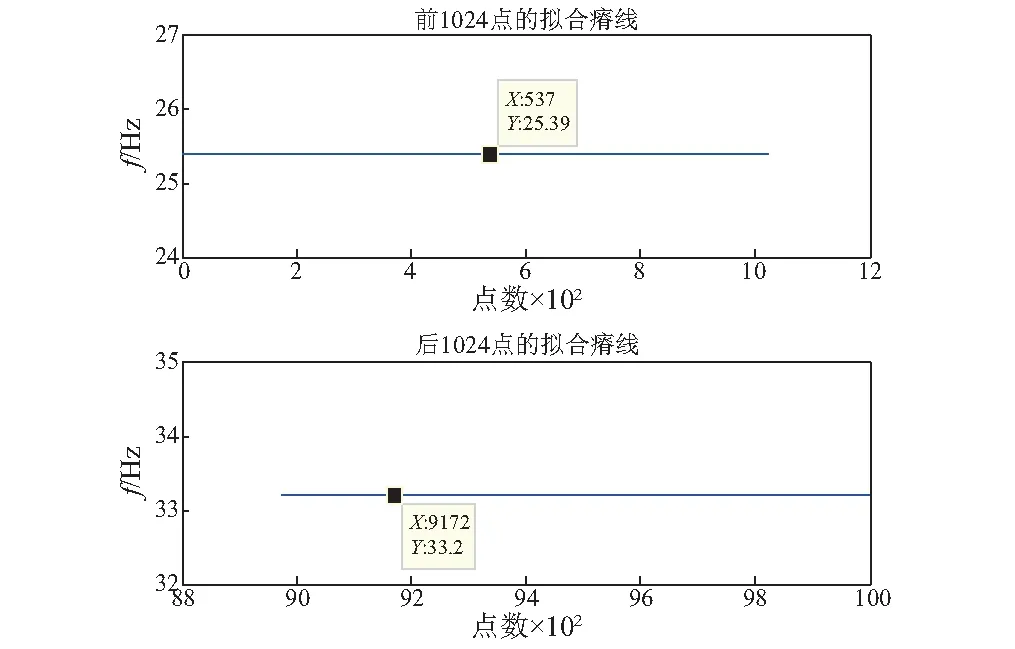
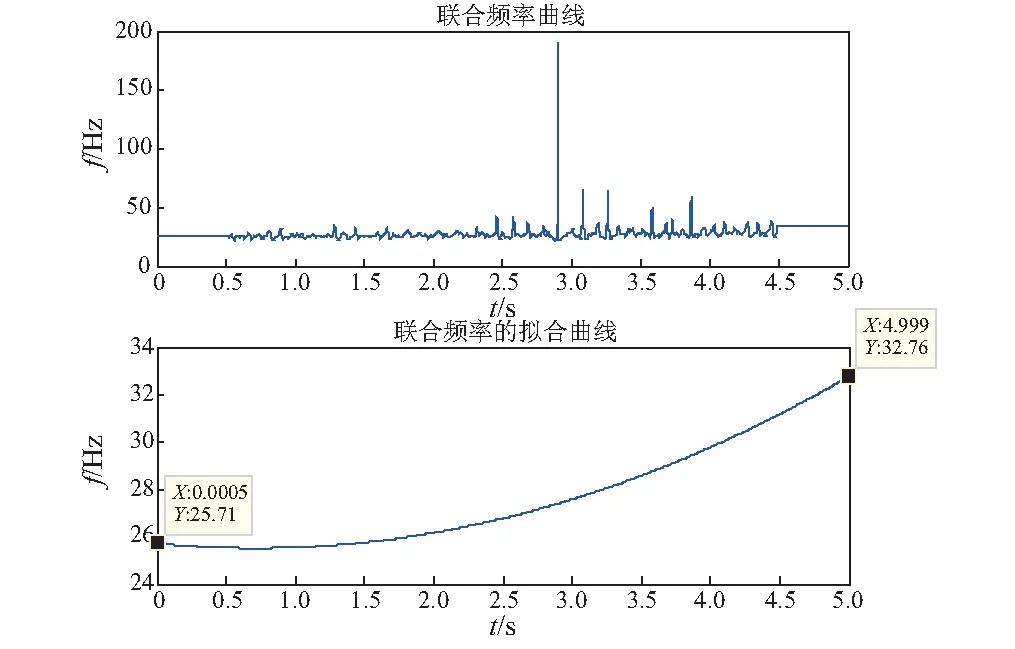
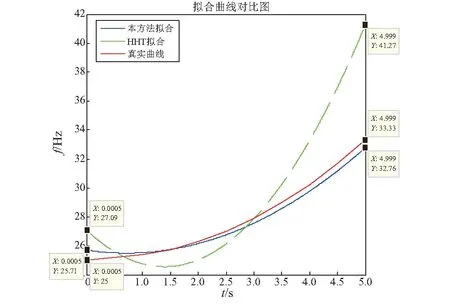
然后，以增速过程为例，对于前端数据，从(ti,fi)中找出满足fd

(9)

(6) 用第5步得到IMF前后两端截取各点的瞬时频率值代替第3步Hilbert变换得到的对应点处的值，组成一个新的频率数组。

(7) 对新的频率数组重新进行最小二乘拟合，获得光滑的转速曲线。

3 应用实例

将本文所提方法应用于某双跨转子平台的转子不平衡故障分析，以实际信号分析来说明本文算法的分析过程，并对其有效性和优越性进行验证。试验中先为质量均匀转子添加适当配重，然后接通电机电源，将转速调至1 500 r/min，待转轴速度稳定时，设定增速至2 000 r/min，并开始采集加速度传感器获得的振动信号。采样速率为2 000 Hz，采样时间为5 s，数据长10 000点。图2为升速阶段转子不平衡状态下振动信号的时序波形图，此信号为典型的非平稳信号，对其直接进行傅里叶变换会出现“频率模糊”的现象，掩盖了部分故障信息，如图3所示。

图2 振动信号时域波形Fig.2 Time domain waveform of vibration signal

图3 振动信号频谱Fig.3 Spectrum of vibration signal

对振动信号直接进行EMD分解，得到的IMF如图4所示。从图中可以看到，相邻IMF间产生了模态混叠现象，使IMF失去了真实意义。

因此，用本文所提方法对参考轴的转速曲线进行估计，之后用于阶比分析，获得阶比谱，检验方法的有效性。首先，设置EEMD中随机白噪声的标准差σ=0.5，执行次数M=200，得到不包含残差在内的共13个IMF，其中IMF1为原始信号，IMF2～13为分解得到的IMF分量，RES为残差，如图5所示。可见，EEMD分解结果中出现了很多虚假分量，需要对其进行筛选。

图4 EMD分解得到的IMFFig.4 IMF obtained by EMD decomposition

图5 EEMD分解得到的IMFFig.5 IMF obtained by EEMD decomposition

分别求各IMF与原始信号的相关系数μi(i=1,2,3,…,13)，如表1所示。由表中数据得，除作为原始信号的IMF1外，IMF4、IMF5和IMF6与原始信号的相关性相对较大。

表1 各IMF与原信号间的相关系数值

计算各IMF的能量值，并做归一化处理，得到如图6所示的能量谱柱状图。由于IMF1为原始信号分量，所以忽略其影响。从图中可以看到，除IMF1外，IMF4、IMF5和IMF6所占比重较大。

图6 能量谱图Fig.6 Energy spectrum

参考文献[14]，设置阈值ε=max(μi)/10，将大于ε的μi所对应的IMF保留下来，认为该IMF与原始信号相关性较好，是真实分量；将小于该阈值的IMF合并到残差中，认为其与原始信号相关性较差，是虚假分量。经过筛选得到的新的IMF，如图7所示。

图7 筛选得到的IMFFig.7 The filtered IMF

筛选后的IMF与EEMD分解得到的IMF对应关系，如表2所示。

表2 筛选后的IMF与原IMF对应关系

由表2可得，除原始信号IMF1外，筛选后的IMF3′与原始信号间的相关系数最大，相关性最好，并且其能量占比也同时达到最大，所以综合相关系数与能量比值，选取IMF3′作为参考轴的振动分量。对IMF3′做Hilbert变换，得到的时频曲线及其拟合曲线如图8所示。可以看到由于Hilbert变换的“端点效应”，IMF3′时频曲线两端频率明显突变，尤其是末端一些点出现了如图中“竖线”所示的极大偏差，其拟合曲线两端的值也因此大幅失真。

图8 Hilbert变换得到的时频曲线及其拟合曲线Fig.8 Time-frequency curve and fitting curve obtained by Hilbert transform

观察IMF3′的时频曲线，分别截取其两端各1 024个点进行时频重排变换。对两个重排矩阵直接进行瘠线提取，得到如图9所示的前后两端截取数据的时频瘠点。从图中可以看出，瘠点有一定的波动，并不都处于转频范围内，应该进行限制条件的瘠线提取。由于转速范围为1 500～2 000 r/min，即转轴频率在25 Hz到33.3 Hz，所以在时频矩阵中设置频率搜索下限fd=24 Hz，上限fu=34 Hz。由本转子平台电机的增速特性，选取m和n的值为2，即对于前端数据，在24～26 Hz内进行搜索；对于后端数据，在32～34 Hz内进行搜索。前后两端数据满足条件的时频瘠点，如图10所示。

图9 两端数据直接提取得到的时频瘠点Fig.9 Ridge points of both ends extracted directly

图10 两端数据满足条件的瘠点Fig.10 Qualified ridge points of both ends

将满足条件的瘠点进行最小二乘拟合，得到前后各1 024点的拟合瘠线，如图11所示。把截取各点拟合得到的瞬时频率值与Hilbert变换得到的瞬时频率值进行“拼接”。由于Hilbert变换得到的数据中间部分的瞬时频率仍有一定波动，所以需要将联合的频率进一步拟合，以得到光滑的转频曲线。联合频率曲线及其二阶拟合得到的光滑转频曲线，如图12所示。

图11 两端数据的拟合瘠线Fig.11 Fitting ridges of both ends

图12 联合频率曲线和其拟合曲线Fig.12 Joint frequency curves and its fitting curves

将HHT方法和本文方法估计的转频曲线与真实曲线作比较，如图13所示。从图中可以看到，前者最大误差为7.94 Hz，最大相对误差率为23.82%；后者最大误差为0.71 Hz，最大相对误差率为2.84%，本文方法的两种参数指标较HHT拟合方法更小，在两端点处明显改善了频率的突变现象，提高了拟合精度，验证了本文方法提取转速曲线相对于HHT方法的优越性。

图13 两种方法估计的转频曲线Fig.13 Speed curve estimated by the two methods

由转频曲线计算重采样时刻，并对原始信号进行等角度重采样，重采样结果如图14所示。之后，对重采样数据作FFT分析，得到如图15所示的阶比谱。从阶比谱中可以看到，信号能量主要集中于基频，但是有明显的二阶和三阶等高次频率存在，整个频谱呈“枞树形”，符合转子不平衡故障的特征，验证了本方法的有效性。

图14 重采样波形Fig.14 Resampling waveform

图15 阶比谱Fig.15 Order spectrum

4 结 论

(1) 针对HHT变换过程中的模态混叠、端点效应，以及传统时频分析时频聚焦性差，计算效率低等问题，提出EEMD-HHT与时频重排相结合的转速曲线估计方法。

(2) 利用该方法对某双跨转子平台的转子不平衡故障进行分析，提取参考轴对应的转频曲线，并与HHT方法直接提取的转频曲线对比，验证了本方法的优越性。将时域非平稳振动信号进行等角度间隔重采样转化为角域平稳信号，获得阶比谱，验证了本文所提方法在阶比分析中的有效性。