基于VMD和SVDD结合的滚动轴承性能退化程度定量评估

姜万录, 雷亚飞， 韩 可,3， 张 生， 苏 晓

(1.燕山大学 河北省重型机械流体动力传输与控制重点实验室，河北 秦皇岛 066004；2.燕山大学 先进锻压成形技术与科学教育部重点实验室，河北 秦皇岛 066004；3.中车南京浦镇车辆有限公司，南京 210031)

滚动轴承是机械设备中非常重要的元件，其发生故障会直接影响到整个机械设备的正常运行，因此对滚动轴承的状态监测和故障诊断也就尤为重要[1- 2]。滚动轴承从开始出现异常到最终失效是一个循序渐进的过程，需要经历不同程度的性能退化阶段[3]。通过采集滚动轴承运行过程中的振动信号，并对信号进行分析处理，从而评估性能退化的程度，便可以合理地制定维修方案。

1998年华裔科学家黄锷(Norden E. Huang)提出了经验模态分解(Empirical Mode Decomposition, EMD)方法，可以将非线性、非平稳信号分解成若干个含有不同频率成分的固有模态函数(Intrinsic Mode Function, IMF)分量，但是其存在着模态混叠、端点效应等缺点[4-5]。变分模态分解(Variational Mode Decomposition, VMD)[6]是由Konstantin Dragomiretskiy于2014年提出的一种自适应信号分析方法，通过设定分解模态个数K，可以将复杂的信号分解为K个不同频率成分的限带固有模态函数 (Band-Limited Intrinsic Mode Function, BIMF) 分量，如果分解模态个数K值选取合适，可以很好地抑制EMD方法中出现的模态混叠现象。

支持向量数据描述(Support Vector Data Description, SVDD)是Tax等[7]提出的一种单值分类方法。它的发展基础是统计学习理论，目前广泛应用于数据异常点检测和设备性能退化评估中。它通过利用给定的训练数据建立一个超球体模型，同类数据被包含在超球体内部，而不属于该类的数据则在超球体的外部[8-10]，通过计算待检样本与超球体球心的距离，可以实现异常点的检测和设备的性能退化评估。

本文提出了一种基于VMD和SVDD结合的性能退化评估方法，首先利用VMD可以自适应地将信号分解成不同频率成分BIMF分量的能力以及SVDD的异常点检测功能，提出基于VMD和SVDD的特征提取方法，提取出准确反映设备不同性能退化程度的特征信息，然后利用SVDD方法对设备进行性能退化评估，并利用隶属函数将性能退化指标划分为不同的性能退化程度范围，实现滚动轴承退化程度的定量评估。

1 变分模态分解

1.1 VMD原理

VMD方法摒弃了EMD方法的循环筛选过程，而使用交替方向乘子法来求得约束变分问题的最优解，在频域内不断更新各个分量的中心频率及带宽，然后使用傅里叶逆变换将各个分量变换成时域信号，由此可以自适应地将原始信号的频域分解成K个窄带调幅调频(AM-FM)分量的叠加。

定义1：限带的固有模态函数(Band-Limited Intrinsic Mode Function, BIMF)：

uk(t)=Ak(t)cos[φk(t)],k=1, 2, …,K

(1)

定义2：根据卡森原理(Carson’s Rule)，BIMF的带宽估计为：

BWAM-FM=2(Δf+fFM+fAM)

(2)

式中:Δf为瞬时频率的最大偏移；fFM为调频信号的最高调制频率；fAM为包络线Ak(t)的最高频率。

为了建立约束变分问题，需要经过以下几个步骤：

(1) 通过Hilbert变换求得各模态函数uk的单边频谱；

(2) 通过乘指数项，将各模态函数的频谱调制到相应的基频带；

(3) 通过计算上述解调信号的2范数，估计各模态的带宽。

约束变分问题为：

(3)

式中:uk=(u1,u2, …,uK)，为各模态函数集；ωk=(ω1,ω2, …,ωK)为各模态中心频率集；∂t为对函数求时间t的偏导数；δ(t)为单位脉冲函数；j为虚数单位；*表示卷积。

为了求得上述约束变分问题的最优解，即各个模态函数分量，引入一个增广拉格朗日函数ζ，如式(4)所示。

(4)

式中:α为二次项的惩罚因子；λ(t)为拉格朗日乘子；f(t)为原信号。

使用交替方向乘子法进行多次迭代搜索找到ζ的极小值点，从而解决式(4)中的最小化问题，进而得到各模态函数和中心频率。

1.2 VMD分解模态个数K的确定

对信号进行VMD分解前，首先要确定分解模态个数K的值。由于VMD分解得到的K个BIMF分量的中心频率是从小到大依次排列的，随着K的增大，各个分量中心频率之间的差值会越来越小，最终会出现过分解现象。所以，可以通过比较K个BIMF分量的中心频率的差值，来判断是否过分解，进而确定分解模态个数K的值。

使用以下仿真信号进行验证：

b=0.4·sin(2π·5·t)+0.3 ·cos(2π·50·t)+
0.2·sin(2π·250t)+η

(5)

式中:η～N(0,σ)为标准差σ=0.1的高斯白噪声，采样频率fs=1 000 Hz，采样点数N=1 000。

选取不同分解模态个数K，分别对仿真信号进行VMD分解，得到各个BIMF分量的中心频率如表1所示。

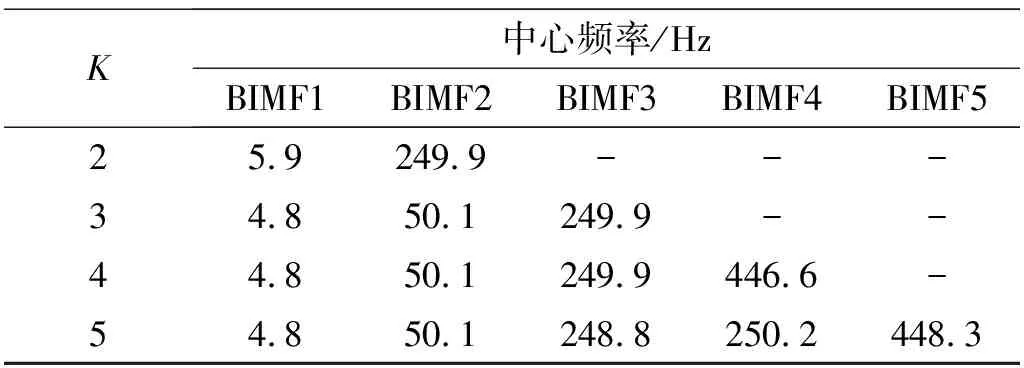
表1 不同K值各BIMF分量中心频率

观察表1可知，随着K值的增大，当K取5时，5个BIMF分量中第一次出现248.8 Hz和250.2 Hz两个相近频率的分量，此时出现了过分解现象，因此，分解模态个数K应取4，当K取4时，仿真信号中的各个频率成分5 Hz正弦信号、50 Hz余弦信号、250 Hz正弦信号以及噪声信号均被有效分解出来。因此，按照观察各个BIMF分量的中心频率之间差值来确定分解模态个数K的方法是有效的。

由于实际信号采样频率高，信号中频率成分多，随着K的增大，不会很快出现中心频率特别接近的BIMF分量，因此根据经验，本文设置一个阈值r，当相邻两个BIMF分量的中心频率的差值小于阈值r时，可以判定此时信号被过分解。通过大量的仿真数据和实测数据的检验，当阈值为0.05倍的采样频率时，分解得到的各BIMF分量可以很好地反映原信号的各频率成分，且不会产生过多的分量，因此取。r=0.05·f

2 支持向量数据描述

SVDD方法是在统计学习理论的基础上发展起来的一种单值分类方法。它首先通过对目标样本{xi,i=1, 2,…,N}进行训练，使用一个非线性映射φ将目标样本映射到高维特征空间内，得到{φ(xi),i=1, 2, …,N}，然后在特征空间内找到一个包含所有或者绝大部分目标样本的最小超球体，超球体内部的点为目标样本，超球体外部的点为非目标样本，即为异常样本，该超球体可以用球心a和半径R来表示。如图1所示为在二维空间内SVDD方法训练得到最小超球体的示意图。

超球体模型的结构风险可以表示为：

F(R,a)=R2

(6)

结构风险最小化的约束条件为：

‖φ(xi)-a‖2≤R2

(7)

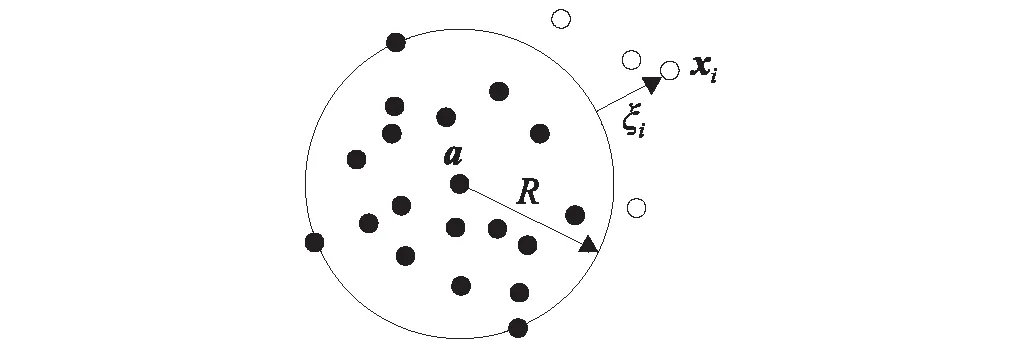
图1 二维空间超球体分类示意图Fig.1 Two dimensional space hypersphere classification sketch

为了避免目标样本内的异常样本对超球体的影响，提高方法的鲁棒性，引入了松弛因子ξ和惩罚参数C，允许部分样本在超球体的外部。此时，上述最小化问题可以表示为：

(8)

引入拉格朗日函数，最小化问题可转化为：

(9)

式中:α,γ为拉格朗日系数。

式(9)分别对R,a和ξ求偏导数，并令其等于0得：

(10)

将式(10)代入式(9)，得到最小化问题式(8)的对偶形式：

(11)

式中:K(xi,xj)为核函数，代替内积运算，即K(xi,xj)=〈φ(xi),φ(xj)〉。SVDD方法中，核函数通常选用高斯核函数：

(12)

当xi=xj时，式(11)中K(xi,xj)=1，算法得到了简化，可以加快SVDD的训练速度。

求解式(11)并结合KKT互补条件，可以得到如下结论：

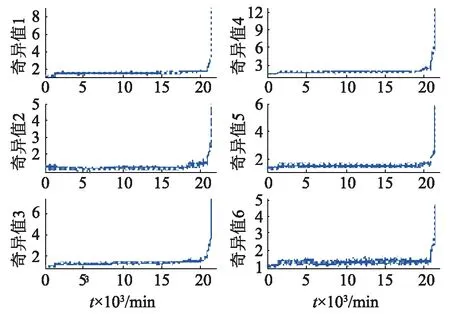
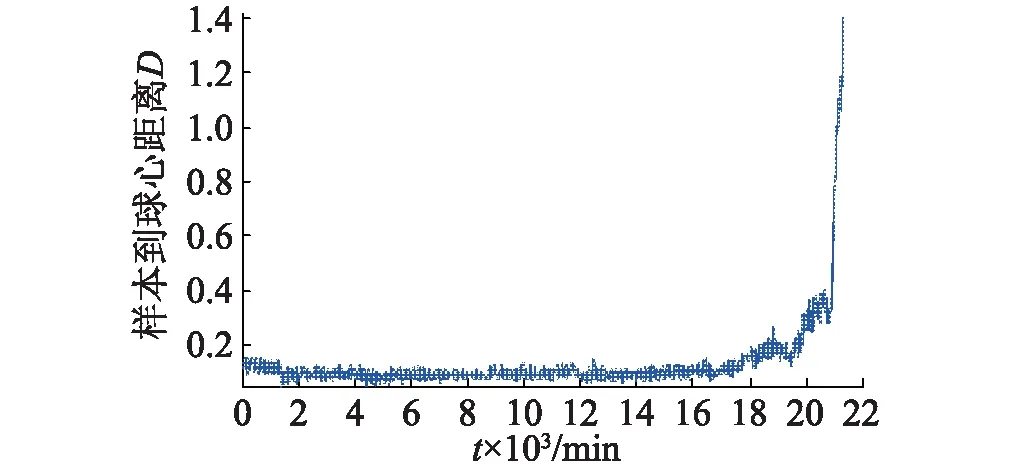
(1) 当αi=0时，‖φ(xi)-a‖2

(2) 当0<αi

(3) 当αi=C时，‖φ(xi-a)‖2>R2，样本在超球体外部，这些样本为异常点；

超球体半径R可以由边界上的任一支持向量xsv距超球体球心a的距离求出：

(13)

同时，任意样本z距超球体球心a的距离D可以通过下式求出：

(14)

比较D与R的大小，如果D≤R，可以判断出样本z与训练样本为同一类；如果D>R，样本z与训练样本不是同一类，即为异常点。

通过计算D与R的差值，可以判断样本z偏离训练样本的程度，差值越大，则越偏离训练样本，根据这个原理，可以将SVDD方法应用在设备的性能退化评估中。

3 基于VMD和SVDD结合的性能退化评估方法

3.1 基于VMD和SVDD的特征提取方法

在设备性能不断退化的过程中，采集到的信号中不同频率成分的能量变化情况也不同，因此，将信号进行VMD分解，得到信号的不同频率成分，然后分别提取出不同频率成分的特征。由矩阵理论可知，矩阵的奇异值是矩阵的固有特征，具有良好的稳定性[11]，当矩阵为一维矩阵时，求得该一维矩阵的奇异值大小可以反映其功率的大小。因此，可以求取不同频率成分BIMF分量的奇异值来组成信号的特征向量。

在信号处理中，当采样时间较长时，采集到的信号中的数据点一般会很多，直接分析会因为数据长度过长而导致运算量过大，通常情况下是截取其中的数千个点用来分析，然而实际上信号中可能会有噪声等异常信号的干扰，如果截取的这一小段信号恰好包含有过多异常信号，分析得到的结果则不可信。针对这种情况，本文提出了如下异常数据样本剔除方法。

对于一个有大量数据点的信号，首先将信号分为m帧，然后分别对每一帧信号进行VMD分解并求出各个BIMF分量的奇异值组成一个特征向量，最终得到一个包含有m个特征向量的特征向量集。使用SVDD方法对该特征向量集进行训练得到最小超球体模型，计算所有特征向量与超球体球心的距离，距离大于超球体半径的特征向量即为异常样本点，设有k个异常样本点，这些异常样本点由于受异常信号干扰，造成提取出的特征向量与其他没受干扰信号的特征向量相差很大，剔除这k个异常样本点，求取剩余(m-k)个特征向量的平均值作为原始信号的特征向量。

对于长信号的分帧，应使每一帧短信号包含有一定数量的故障频率周期。如果分帧数量过多，每帧信号包含的数据点过少，可能无法完整反映信号的故障信息；如果每帧信号包含的数据点过多，则不能有效剔除异常样本点。

以美国辛辛那提大学实测的一组内圈故障轴承信号[12]为例，采样频率fs=20 kHz，采集时间为1.024 s，每个样本中有20 480个数据点，任取其中一个样本。首先确定VMD的分解模态个数K值，不同K值对应的各BIMF分量的中心频率,如表2所示。

表2 实验数据的BIMF分量中心频率

设阈值r=0.05·fs=1 000Hz，随着K增大，当K取7时，BIMF2和BIMF3中心频率的差值为958.7 Hz，各个分量中心频率的差值首次小于阈值r，因此取VMD的分解模态个数K= 6。

将信号分为20帧，每帧信号中有1 024个数据点，如图2所示。通过计算，轴承内圈故障频率为296.9 Hz，每帧信号中包含有296.9×1.024/20=15.2个故障周期，可以完整地反映故障信息并能有效剔除内圈故障信号的离群点。

图2 信号分帧示意图Fig.2 Signal framing sketch

分别使用VMD方法将20帧信号分解成6个BIMF分量，经Hilbert包络解调后求出奇异值，构成含有20个6维特征向量的特征向量集，如图3所示。

图3 各帧信号特征向量及均值Fig.3 Feature vectors of each frame signal and the average value

图3中粗虚线为20个特征向量的平均值。可以看出，20个特征向量中，有3个特征向量比其他特征向量大很多，对应的短信号分别为s1、s15和s17。使用SVDD方法对20个特征向量进行训练，找到其中的3个异常样本点并剔除，然后求出剩余特征向量的平均值，并与剔除异常样本点之前所有特征向量的平均值进行对比，如图4所示。

图4 剔除异常点前后特征向量均值对比Fig.4 Comparison of feature vectors average value before and after removing outliers

图4中，下方粗实线为剔除异常样本点后，求得的特征向量的平均值，上方粗虚线为不剔除异常样本点，直接求得所有特征向量的平均值。可以看出，剔除异常样本点后求得的平均值比直接求得的特征向量平均值小，免受几个很大的异常特征向量的影响，能够更好地反映原始信号的特征。

3.2 性能退化评估流程

对于一组包含设备从正常运行到发生故障之间各个退化状态的全寿命样本，为了从中获取设备的性能退化程度，本文提出了基于VMD和SVDD结合的性能退化评估方法，性能退化评估流程图如图5所示。

(1) 将全寿命样本内每一个长信号都分为m帧短信号，然后分别使用VMD分解并提取特征向量，每个样本分别对应一个含有m个特征向量的特征向量集。

(2) 使用SVDD方法对每个特征向量集进行训练得到一个最小超球体，计算特征向量集中每个特征向量与超球体球心的距离，距离大于超球体半径的即为异常样本点，找到这些异常样本点并剔除，对剩余的特征向量求平均。此时，每个样本分别得到一个特征向量，即为全寿命样本的特征向量。

图5 性能退化评估流程图Fig.5 Flow chart of performance degradation assessment

(3)由于在设备的全寿命周期中，正常运行阶段相对于性能退化阶段往往占有更长的时间，且正常运行阶段设备的各项性能基本保持不变。因此，可以从全寿命样本特征向量中初步找出正常状态特征向量，取出其中一部分作为SVDD的训练样本。

(4) 使用SVDD方法对正常样本进行训练，在高维特征空间内找到包含正常状态特征向量的最小超球体，即为SVDD超球体模型。

(5) 将全寿命样本特征向量输入所建立的SVDD超球体模型中，计算得到每个样本与超球体球心的距离D。

(6) 对于不同的故障类型和故障程度，通过采集到的数据分析处理得到的SVDD超球体模型以及每个样本与超球体球心的距离指标的大小及变化情况不同，因此，引入隶属函数，将不同样本的性能退化程度转化为与正常状态样本的隶属度，作为刻画性能退化的指标PI(Performance Index)。本文使用的是降半柯西型隶属函数：

(15)

式中:a,b>0。

令x为样本到超球体球心的距离D，c为超球体半径R，根据实际情况调整参数a和b，以隶属度μ(D)为性能指标，得到全寿命性能退化曲线，并将隶属度值进行分级，以确定性能退化的程度。

4 实验验证与分析

本文使用美国辛辛那提大学公布的滚动轴承内圈故障全寿命数据，来验证基于VMD和SVDD结合的性能退化评估方法的有效性。图6和图7分别为进行轴承全寿命实验的实验简图和传感器布置图。

图6 实验简图Fig.6 Experimental diagram

图7 传感器布置图Fig.7 Sensor layout diagram

实验系统由电机驱动，通过带传动将力矩传递给转轴，轴转速为2 000 r/min，转轴上安装有4个相同的轴承，轴承型号为ZA-2115，轴承节圆直径为7.15 cm，滚动体直径为0.84 cm，接触角为15.17°。轴承的润滑方式为强制润滑，使用安装在轴承外圈上的4个电热偶监测轴承的温度，从而调节润滑油流量。同时使用弹性装置对每个轴承施加26 670 N的径向载荷。每个轴承在水平方向和竖直方向分别安装一个振动传感器，用来采集水平和竖直方向的振动信号，传感器型号为PCB353B33。使用的数据采集卡为NI公司DAQCard-6062E型号采集卡，每隔10 min采集一个样本，采样频率为20 kHz，每次采集时间为1.024 s。

本文使用的是轴承3内圈失效数据。采集了轴承3从正常运行到内圈失效全寿命过程的数据，共采集到了2 134个样本，每个样本内包含有20 480个数据点，全寿命信号采集时间跨度为21 340 min。

对于内圈失效的全寿命样本，首先需要确定VMD方法的分解模态个数K。分别取5 000 min、10 000 min、15 000 min和20 000 min时刻的样本，确定分解模态个数K。

分别使用不同K值对5 000 min时刻的样本进行VMD分解，不同K值对应的各BIMF分量的中心频率如表3。

表3 5 000 min时刻样本的BIMF分量中心频率

设定阈值r=0.05·fs=1 000 Hz，随着分解模态个数K值增大，当K取7时，BIMF1和BIMF2中心频率的差值为615.9 Hz，各个分量中心频率的差值首次小于阈值r，因此，取VMD的分解模态个数K=6。

使用同样方法确定10 000 min、15 000 min和20 000 min时刻样本的分解模态个数K，其值均为6，因此，使用VMD方法对全寿命样本进行分解时，取分解模态个数K=6。

将全寿命样本中每个样本信号都平均分为20帧短信号，每帧信号中有1 024个数据点，信号分帧图如图2所示。对于每一个样本，分别使用VMD方法将20帧短信号分解成6个频率成分由低到高的BIMF分量，每个分量经Hilbert包络解调后再求出6个奇异值，构成含有20个特征向量的特征向量集。使用SVDD方法找到并剔除所有特征向量集内的异常样本点，然后对剩余特征向量求出平均值，最终得到含有2 134个6维特征向量的全寿命特征样本集。6个BIMF分量对应的6个奇异值在全寿命过程中的变化情况，如图8所示。

图8 各BIMF分量奇异值全寿命过程的变化趋势Fig.8 The change trend of singular values calculated from each BIMF component in the complete life cycle

由图8可以看出，各个奇异值在前17 000 min一直保持平稳，均没有明显的波动，即为正常运行状态，取前15 000 min即前1 500个样本的特征向量作为SVDD的训练样本。

训练样本经SVDD方法训练后得到包含有正常状态特征向量的最小超球体模型，超球体的半径R=0.152 9。将全寿命2 134个样本输入训练所得的超球体模型中，得到每个样本到超球体球心的距离D的变化趋势，如图9所示。

图9 全寿命样本到球心的距离Fig.9 Distances?from complete life samples to the sphere center

由图9可以看出，轴承从开始运行到最终发生故障大致可以分为4个阶段，可以将其划分为：正常状态、轻度故障状态、中度故障状态和重度故障状态。

引入降半柯西型隶属函数，将隶属度作为性能退化指标，用于定量刻画性能退化程度。

(16)

式中：R= 0.152 9。

为了便于观察、计算和统计，通过调整参数a,b，使得μ(D)在指定范围内分布。取a=2.65，b=1，此时μ(D)的范围及对应的运行状态如下：

当μ(D)=1时为正常状态，μ(D)=0.8～1时为轻度故障状态，μ(D)=0.6～0.8时为中度故障状态，μ(D)<0.6时为重度故障状态。

将隶属度μ(D)作为性能退化指标PI，得到全寿命性能退化曲线，如图10所示。

图10 性能退化曲线Fig.10 Performance degradation curve

由图10可以看出，在17 730 min之前，性能退化指标PI一直为1，此时轴承为正常状态；17 730 min后，PI开始小于1，一直到19 840 min，PI基本都在0.8～1范围内波动，此时轴承为轻度故障状态；从19 850 min到20 970 min，PI一直在0.6～0.8范围内波动，此时轴承为中度故障状态；从20 980 min开始到最后，PI一直小于0.6，轴承达到了重度故障状态。

5 与传统时域特征指标分析结果的对比

本节使用波形指标Sf、峰值指标Cf、脉冲指标If、裕度指标CLf、峭度指标Kf五个无量纲传统时域特征与前面提出的基于VMD和SVDD的特征提取方法作对比。

对于内圈失效全寿命样本，分别从每个样本的20 480个数据点中截取4 096个点作为待分析信号，所有信号经Hilbert包络解调后分别提取出上述五个无量纲时域特征，组成2 134个5维的全寿命特征向量集，5个特征在全寿命过程中的变化情况，如图11所示。

图11 传统时域特征全寿命过程的变化趋势Fig.11 The change trend of traditional time domain features in the complete life cycle

由图11可以看出，五个特征在前17 000 min内基本没有变化，选取前15 000 min五个特征作为SVDD的训练样本。

使用SVDD方法对训练样本进行训练，得到包含有正常状态特征向量的最小超球体模型，超球体的半径R=0.166 0。将全寿命2 134个样本输入超球体模型中，得到每个样本到超球体球心的距离D，如图12所示。

图12 传统时域特征全寿命样本到球心距离Fig.12 Distances from complete life samples obtained from traditional time domain features to the sphere center

由图12可以看出，在18 040 min之前，样本到超球体球心的距离D一直小于超球体半径R，即0.166 0(图12中虚线)，在这期间轴承为正常状态，从18 040 min往后，距离D持续有较大波动，最后一段时间却又趋于稳定变得很小，无法区分性能退化的程度。因此，本文提出的特征提取方法与传统的时域特征提取方法相比，更具有优势。

6 结 论

(1) 采用VMD分解得到的各BIMF分量的奇异值作为特征，可以很好地反映信号各个频率成分的功率大小。

(2) 在特征提取时将长信号进行分帧处理并结合SVDD方法的异常点检测功能，能够有效解决当采样时间长，采集到的信号数据点多时，信号中某些部分可能受到异常信号干扰的问题。

(3) 采用隶属函数对全寿命样本到球心距离进行处理，以隶属度作为性能退化指标，可以定量地评估轴承性能退化程度。

(4) 利用滚动轴承全寿命数据对基于VMD和SVDD结合的性能退化评估方法进行了验证，得到性能退化曲线很好地对不同的性能退化程度进行划分，非常清晰地反映出滚动轴承的性能退化过程。

(5) 使用传统时域无量纲特征与本文提出的基于VMD和SVDD的特征提取方法作对比，进一步验证了本文方法的优越性。