含弱界面的多铁性空心层合柱内径 对振动行为的影响
潘晶雯, 罗 静, 姜广绪, 鞠丽梅, 张少亮
(1. 陆军装甲兵学院车辆工程系, 北京 100072; 2. 陆军装甲兵学院教研保障中心, 北京 100072; 3. 中国能源建设集团规划设计有限公司, 北京 100120)
多铁性层合柱是一类应用于智能器件中的常见多铁性结构形式。对于层合柱,界面是关键部位,它起着磁电耦合的应变介导作用[1]。在动态载荷环境中,多铁性智能结构常处于振动的工作状态,而在力-电-磁耦合作用下,其界面容易产生机械损伤、电学损伤、磁学损伤等界面损伤。界面损伤会在一定程度上削弱界面和结构的功能,也势必影响层状多铁性器件的力-电-磁响应特性。因此,振动条件下含损伤界面的智能结构力学研究成为近年来国内外的研究热点[2-10]。
目前,界面损伤模型一般都是解耦的线性模型,而忽略了不同种类损伤之间的耦合作用。在含弱界面的多铁性层合结构研究中,损伤耦合条件下进行力学分析更符合实际情况。基于此,笔者利用平面问题中的弱界面耦合广义线弹簧模型对含弱界面的多铁性空心层合柱振动行为进行分析,以探究空心层合柱内径变化影响界面损伤系数和损伤耦合系数对机械振动频率的作用规律,为空心柱状智能元器件的尺寸设计提供一定的理论依据。
1 含弱界面的多铁性层合柱的耦合广义线弹簧模型
在高温、高压条件下,多铁性材料制造时2种材料之间因相互渗透或者扩散,而在接触面产生界面层,即弱界面[3],这种作用使得界面层同时含有铁电、铁磁成分。因此,在无力、电、磁损伤存在的情况下,该类界面层一般具有磁电弹性质,其平面问题的本构关系为[11]
σr=Mu,
(1)
式中:σr=[σrBrDr]T,为广义应力,其中σr、Br、Dr分别为径向的正应力、磁感应强度、电位移;u=[urφrφr]T,为广义位移,其中ur、φr、φr分别为径向的机械位移、磁势、电势;
为将界面层的材料系数矩阵与广义位移偏导运算联立得到的矩阵,其下标中的逗号后表示对相应坐标求偏导运算所针对的变量,c33、μ33、ε33、h33、e33、d33分别为界面层的弹性常数、磁导率、介电系数、压磁系数、压电系数、磁电系数。
在机械载荷和电磁场作用下,含弱界面的多铁性层合柱的耦合广义线弹簧模型为[12]
σr|Γ=βΓ(u|Γ+-u|Γ-),
(2)
式中:
(3)
为广义刚度矩阵,其中β2为机械损伤系数,β3为磁学损伤系数,β4为电学损伤系数,β5、β6和β7分别为力-磁损伤耦合系数、力-电损伤耦合系数和力-磁-电损伤耦合系数;u|Γ+、u|Γ-分别为弱界面上铁磁侧、铁电侧的广义位移。
由于βi(i=2,3,…,7)的量纲彼此不同,为便于分析,将式(3)改写为
(4)
2 含弱界面的多铁性层合柱的理论模型
2.1 几何模型
图1为一个含弱界面的空心多铁性层合柱的横截面,其中外部为铁电层,内部为铁磁层,中间为弱界面。以横截面圆心O为原点建立极坐标系,θ为半径r和极轴Ox的夹角。铁磁层内、外半径分别为r0、r1,铁电层内、外半径分别为r1、r2。于是,铁磁层、铁电层的厚度分别为tm=r1-r0,te=r2-r1。
该多铁性层合柱位于径向电场中,其内、外表面的径向电场分量的大小分别为E1和E2。在铁磁层的内表面加以接地,而在铁电层的外表面加以φ0eiωt的交流电压,其中φ0为提供电势的振幅,ω为交流电压的角频率,t为时间。为了简便,在后面的说明中消去时间因子,则多铁性层合柱的边界条件为
(5)
(6)
另外,在设置层合柱的内、外表面的边界条件后,也需对弱界面的相关参数进行连续性假设,则有

σr(r1)=βΓ(u(2)(r1)-u(1)(r1))。
(7)
2.2 基本方程
2.2.1 压电部分
压电部分的基本方程如下:
(8)
(9)
(10)
(11)
弹性力学的平衡方程为
(12)
(13)
(14)
将式(13)进行积分可得
(15)
将式(15)代入式(10),可得
(16)
将式(8)、(9)代入式(12),可得
(17)
式中:A1为积分常数;η=ωr/v2,为定义的无量纲量,v2为常数(见附录A);α2、λ2为常数(见附录A)。
二阶非齐次微分方程的解为[13]
A1λ2(γ1h(η)+γ2l(η)),
(18)
式中:A2、A3为积分常数;Jα2(η)、Yα2(η) 为α2阶第一类和第二类Bessel函数;γ1、γ2为常数(见附录A);h(η)、l(η)为已知函数(见附录B)。
将式(18)代入式(8)中,化简后可得
(19)
对式(16)进行积分,化简后可得
φr(2)=f21(η)A1+f22(η)A2+A3f23(η)+A4;
(20)
对式(14)进行积分可得
(21)
将式(21)代入式(11),可得
(22)
式中:g21(η)、g22(η)、g23(η),f21(η)、f22(η)、f23(η)均为已知函数(见附录B);A4、B1、B2为积分常数。
2.2.2 压磁部分
压磁部分的计算推导与压电部分相似。同理,其基本方程为
(23)
(24)
(25)
(26)
推导得到如下结果:
(27)
(28)
(29)
C1λ1(γ11h1(ξ)+γ22l1(ξ)),
(30)
(31)
(32)
式中:C1、C2、C3、C4、D1、D2为积分常数;Jα1(ξ)、Yα1(ξ) 为α1阶第一类和第二类Bessel函数,其中ξ=ωr/v1,为定义的无量纲量,α1、v1为常数(见附录A);λ1、γ11、γ22为常数(见附录A);g11(ξ)、g12(ξ)、g13(ξ)、h1(ξ)、l1(ξ)、f11(ξ)、f12(ξ)、f13(ξ)均为已知函数(见附录B)。
2.2.3 振动分析
将式(8)-(11)、(20)、(22)和式(27)-(32)代入式(5)-(7)中,得到代数方程
MF=C。
(33)
式中:
F=(A1,A2,A3,A4,B1,B2,C1,C2,C3,C4,D1,D2)T;
C=(0,0,0,0,0,φ0,0,0,0,0,0,0)T;
M=(mij)12×12,矩阵中各元素表达式见附录C。
根据式(15)、(33),电位移可以表示为
(34)
式中:N=(nij)12×12,其中nij=mij(i=01,02,…,12;j=02,03,…,12),n0101=n0201=…=n0501=0,n0601=φ0,n0701=n0801=…=n1201=0。
3 数值分析结果
假设铁电层和铁磁层的材料分别为BaTiO3和CoFe2O4[11,14]。另外,假设铁电层与铁磁层具有相同的厚度,即t=te=tm=0.01 m。
3.1 多铁性层合柱内径对界面损伤的影响
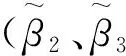

3.2 多铁性层合柱内径对弱界面损伤耦合的影响
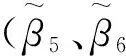
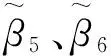
3.3 多铁性层合柱的径厚比对机械振动频率的影响
由3.1、3.2节可知:当内径r0=0.08 m时,弱界面损伤系数及损伤耦合系数对机械振动频率的影响很小。因此,有必要研究层合柱的径厚比n=r0/t对机械振动频率的影响。
图8为在不同的弱界面损伤系数及损伤耦合系数存在的情况下,径厚比n对机械振动频率的影响变化曲线。可以看出:随着n的不断增大,各损伤系数及损伤耦合系数对机械振动频率的影响呈下降趋势;当n≈8时,各系数对振动频率的影响已很小,且趋于稳定。
4 结论
针对多铁性复合材料力电磁耦合的特征,利用含弱界面多铁性层合柱的耦合广义线弹簧模型,对指定参数的空心多铁性层合柱进行了振动分析。结果表明:当空心层合柱的径厚比n≈8时,界面损伤系数及损伤耦合系数对机械振动频率的影响很小。此结论可为空心柱状各铁性智能器件的尺寸优化设计提供一定的理论依据。
附录A:常数
(A-1)
(A-2)
(A-3)
(A-4)
式中:Γ(x)为Gamma函数。
附录B:已知函数
(B-1)
(B-2)
式中:pFq[{a1,…,ap},{b1,…,bq},x]为广义超几何函数,其中p为包含a1,…,ap的参数,q为包含b1,…,bq的参数,这里p=1,q=2。
(B-3)
式中:
Ω21(η)=η-1Γ(1-α2)J-α2(η)Jα2(η);
Ω22(η)=ηα2pFq[{α2/2},{1+α2,1+
α2/2},-η2/4]Ω20(η);
Ω20(η)= [Yα2-1(η)-Yα2+1(η)-
(Jα2-1(η)-Jα2+1(η))cot(α2π)];
Ω23(η)=η-1Γ(1+α2)Jα2(η)×
(Yα2(η)-Jα2(η)cot(α2π));
Ω24(η)=η-α2(Jα2-1(η)-Jα2+1(η))×
pFq[{-α2/2},{1-α2,1-α2/2},-η2/4];
Ω25(η)=η-1(γ1h(η)+γ2l(η));
(B-4)
式中:
(B-5)
式中:
Ω10(ξ)= Yα1-1(ξ)-Yα1+1(ξ)-
(Jα1-1(ξ)-Jα1+1(ξ))cot(α1π);
Ω11(ξ)=ξ-1Γ(1-α1)J-α1(ξ)Jα1(ξ);
Ω12(ξ)=ξα1pFq[{α1/2},{1+α1,1+
α1/2},-ξ2/4]Ω10(ξ);
Ω13(ξ)=ξ-1Γ(1+α1)Jα1(ξ)(Yα1(ξ)-
Jα1(ξ)cot(α1π));
Ω14(ξ)=ξ-α1(Jα1-1(ξ)-Jα1+1(ξ))×
pFq[{-α1/2},{1-α1,1-α1/2},-ξ2/4];
(B-6)
式中:
附录C:矩阵元素
m0101=m0102=m0103=m0104=m0105=m0106=0,
m0110=m0111=m0112=0;
m0201=m0202=m0203=m0204=m0205=m0206=
m0207=m0208=m0209=m0210=0,
m0301=m0302=m0303=m0304=m0305=m0306=0,
m0311=m0312=0;
m0406=m0407=m0408=m0409=m0410=
m0411=m0412=0;
m0506=m0507=m0508=m0509=m0510=
m0511=m0512=0;
m0604=1,m0605=m0606=m0607=
m0608=m0609=m0610=m0611=m0612=0;
m0704=m0705=m0706=0,
m0808=m0809=m0810=m0811=m0812=0;
m0906=m0907=m0908=m0909=

