双源平行激光光幕系统安装误差分析
徐 达, 高 源, 李子民
(1. 陆军装甲兵学院兵器与控制系, 北京 100072; 2. 陆军第五综合训练基地, 甘肃 武威 733000)
射击密集度是评定武器性能的一项重要指标,对其进行有效测试具有十分重要的意义[1],为此研发了多种测试靶,包括声靶[2]、光幕靶[3]、CCD靶[4]等,其中光幕靶以光幕作为测试靶面,当有弹丸过靶时,将遮挡部分光幕形成投影,光电检测器件可以测得投影参数,对投影参数进行处理,能够确定弹丸过靶坐标,实现弹丸射击密集度测试[5]。每分钟射速万发以上的弹幕武器具有射频高、初速大的特点,为了实现对其射击密集度的有效测试,需要一种高灵敏度、高精度的测试靶[6-7]。激光具有亮度高、方向性和相干性好、能量集中的特点,以其作为光源构成的光幕靶能够满足弹幕武器射击密集度测试要求[8-9],为此笔者设计了一种双源平行激光光幕系统,用于弹丸射击密集度测试。
在光幕测试系统中,存在多种影响测试结果的因素,为了改善测试系统性能,保证测试结果真实可信,需要对这些影响因素进行研究。蔡荣立等[10]分析了炮口焰在光幕测试中的影响,并利用光电补偿部件和信号处理电路消除了干扰信号;张智诠等[11]研究了弹丸激波在光幕靶测试中的影响,并根据弹丸飞行姿态对测试结果进行了数据修正;高芬等[12]分析了弹丸着靶位置、靶距、幕面夹角、靶面大小、弹丸斜入射角等对四光幕精度靶测试结果的影响,为后续系统的设计安装提供了依据;贾云飞等[13]分析了光能分布均匀性对测试结果的影响,并对光幕靶进行了改进,提升了光幕中光能分布的均匀性,保证了测试结果的真实准确。除了上述各类影响因素外,安装误差也会对测试结果造成影响。安装误差不可避免,但可以通过调节将其对测试结果造成的影响控制在可接受范围内。为此,笔者以双源平行激光光幕系统为研究对象,分析了不同安装误差对射击密集度测试结果的影响,可为激光光幕系统安装调试提供依据,并保证激光光幕测试系统可有效完成弹幕武器射击密集度测试。
1 激光光幕系统
1.1 系统构成
为了实现弹幕武器射击密集度的有效测试,构建了一种双源平行激光光幕系统。图1为单源激光光幕,线激光器被搭载平台固定在空中,用于生成一个三角形光幕,激光检测阵列安装在地面,用于接收激光信号,二者组合使用,构成单源激光光幕。
双源平行激光光幕系统如图2所示,在垂直于弹丸飞行方向的平面内,安装了2个反向对称的单源激光光幕,同时二者沿弹丸飞行方向呈前后分布。从弹丸飞行方向看去,二者存在部分重叠,这个重叠部分即可作为测试靶面,不过考虑到测试靶面的形状多为方形,因此最终选择光幕重叠部分中的四边形作为有效靶面。当有弹丸过靶时,将会遮挡部分光幕,并在2个检测阵列上生成投影,由于激光检测阵列由呈阵列排布的光电二级管构成,因此可以对光电二极管依次进行编号,进而将激光检测阵列作为长度测量工具,实现对投影信号位置参数的测量。在投影参数已知的情况下,将其代入坐标解算模型,就可以实现弹丸过靶坐标的测试。
1.2 弹丸过靶坐标解算模型
图3为弹丸过靶坐标解算图,取激光检测阵列所在直线为x轴,过光源的垂线为y轴,两轴交点为原点O,构建直角坐标系。设2个光源点分别为点P、Q,有效靶面为矩形OGIJ,点D为弹丸截面圆心。当弹丸穿过光幕时,将会遮挡部分光幕,并在检测阵列上形成投影。取点D为弹丸过靶坐标,直线PA、PB、QE、QF为弹丸截面的切线,直线AB和EF为弹丸在检测阵列上形成的投影,点C为直线PD与x轴的交点,点H为直线QD与x轴的交点。
设直线OA、OB、GE、GF的长度分别为a、b、c、d,直线OP的长度为l,直线OG的长度为m,由此计算得到弹丸过靶坐标D(xD,yD)为
(1)
式中:
当检测阵列存在安装误差时,其与光源之间的相对位置发生改变,弹丸投影随之变化,最终影响测试结果。由于测试系统中2个光幕是对称分布的,因此只需对一侧检测阵列的安装误差进行分析,另一侧检测阵列安装误差造成的影响可以通过对应关系转换得到。
当存在安装误差时,单侧检测阵列会偏离标准位置,使得测试数据发生变化,此时a变为an,b变为bn,而c和d仍保持原值,由此求得弹丸过靶坐标Dn(xDn,yDn)为
(2)
式中:
2 检测阵列安装误差分析
取激光光幕系统有效靶面大小为1 m×1 m,被测弹丸直径为30 mm,可接受测试误差最大值为6 mm,分别对左侧检测阵列上下偏移、上下偏转、前后偏转和3种情况共同作用下的测试坐标误差分布情况进行分析。
为了能够得到具体数值,利用MATLAB进行了仿真分析,工作原理如下:假定实际过靶坐标已知,则根据式(1)、(2)可以求出对应的测试坐标,再将2组坐标进行对比,求得的结果就是测试误差。利用上述思路对靶面内所有坐标点进行相同处理,最终可以得到测试坐标误差分布情况。
需要注意的是,由于弹丸本身具有一定尺寸,因此以有效靶面四条边为基准,向内会存在4个宽度为r的矩形,该部分靶面为无用靶面,如图4所示,当弹丸圆心位于这部分靶面时,只有部分弹体进入了测试靶,导致形成的投影不属于完整弹丸,不能用于弹丸坐标的求解。因此在进行坐标误差分析的过程中,无论是x坐标还是y坐标,用于分析的坐标范围都小于实际靶面,由0到m变为由r到m-r,只有弹丸圆心位于上述范围时,得到的数据才与实际情况相符。m和r的大小取决于有效靶面大小和弹丸直径,本文中效靶面大小为1 m×1 m,被测弹丸直径为30 mm,因此m取值为1 000 mm,r取值为15 mm。
2.1 上下偏移误差
由于定位不当和人为因素的影响,在安装过程中,检测阵列在竖直方向上会出现整体偏移的情况,偏移后的位置相较于标准位置偏高或者偏低。设偏移距离为h,当检测阵列向上偏移时,h取值为正;当检测阵列向下偏移时,h取值为负。检测阵列上下偏移时投影分布如图5所示。
发生偏移后,检测阵列起点变为O1,弹丸投影变为A1B1,由此测得的投影参数随之发生变化,其中a变为a1,b变为b1,a1和b1分别为
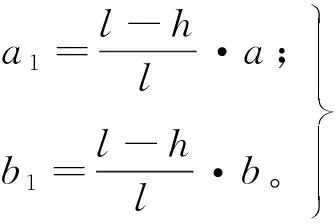
(3)
将式(3)代入式(2),再与式(1)联立求解,可以确定测试坐标误差,通过代入不同数值的h,得到多组测试坐标误差分布,对结果进行对比,得出当h的绝对值限定在4 mm以内时,可以保证最大误差不超过6 mm,其对测试坐标造成的影响在可接受的范围内。取h=4 mm,得到x、y坐标误差分布如图6所示。
当检测阵列向上偏移时,其上的投影整体向左偏移,由此确定的直线PC相较于实际位置向左偏转,此时求得的坐标点位于真实值的左下方,因此x、y坐标的误差均为负值;反之,当检测阵列向下偏移时,则求得的误差均为正值。而由图6可知:当检测阵列上移4 mm时,求得的Δx和Δy均为负值,与理论分析相符。对计算结果取绝对值,x坐标最大误差为1.10 mm,y坐标最大误差为5.64 mm,表明当检测阵列上下偏移时,对y坐标的影响较大。
2.2 上下偏转误差
在激光光幕系统安装调试过程中,检测阵列在竖直方向上会出现上下偏转的情况,即以左侧端点作为原点,在竖直方向上的上下偏转。设偏转角为γ,当检测阵列向上偏转时,γ为正值;当检测阵列向下偏转时,γ为负值,图7为检测阵列向上偏转时投影分布。
发生偏转之后,检测阵列起点仍为点O,弹丸投影变为A2B2,由此测得的投影参数随之发生变化,其中a变为a2,b变为b2,a2和b2分别为
(4)
将式(4)代入式(2),再与式(1)联立求解,可以确定测试坐标误差,通过代入不同数值的γ,得到多组测试坐标误差分布,对结果进行对比,得出当γ的绝对值限定在10′以内时,可以保证最大误差不超过6 mm,其对测试坐标造成的影响在可接受的范围内。取γ=10′,得到的x、y坐标误差分布如图8所示。
当检测阵列向上偏转时,检测阵列上各个点不同程度偏离原有位置,其中距离左侧端点越远的点,偏离程度越大,此时获得的弹丸投影相较于实际值发生了左移,由此确定的x、y坐标均小于实际值,求得的坐标误差均为负值;反之,当检测阵列向下偏转时,则求得的坐标误差均为正值。由图8可知:当检测阵列向上偏转时,求得的Δx和Δy均为负值,与理论分析相符。对计算结果取绝对值,x坐标最大误差为0.84 mm,y坐标最大误差为3.98 mm,表明当检测阵列上下偏转时,对y坐标的影响较大。
2.3 前后偏转误差
检测阵列出现前后偏转的原因与上下偏转相同,这时检测阵列以左侧端点为原点,在水平面内进行转动,设转角为λ。以标准位置为基准,在角度大小相同的情况下,检测阵列向前偏转和向后偏转时得到的投影具有对称性,因此只对其中一种情况进行分析。从空中俯视检测阵列,向后偏转时投影分布如图9所示。
发生偏转后,检测阵列起点仍为点O,弹丸投影变为A3B3,由此测得的投影参数随之发生变化,其中a变为a3,b变为b3,a3和b3分别为
(5)
将式(5)代入式(2),再与式(1)联立求解,可以确定测试坐标误差。通过代入不同数值的λ,得到多组测试坐标误差分布情况,对结果进行对比,得出当λ的绝对值限定在1°以内时,可以保证最大误差不超过6 mm,其对测试坐标造成的影响在可接受的范围内。取λ=1°,得到的x、y坐标误差分布如图10所示。
当检测阵列前后偏转时,偏转后获得的投影相较于原有位置右移,由此确定的直线PC相较于实际位置向右发生了偏转,求得的坐标误差均为正值,表明测得的坐标值大于实际值。由图10可知:当检测阵列向后偏转1°时,Δx和Δy均为正值,与理论分析相符。其中Δx的最大值为0.84 mm,Δy的最大值为1.96 mm,表明当检测阵列前后偏转时,对测试结果的影响较小。
2.4 综合误差分析
对前3种情况共同作用下的测试坐标误差进行分析,得到一组新的误差值,其中x、y坐标误差分布如图11所示。
在对测试结果取绝对值后,得到x、y坐标误差最大值分别为1.19 mm和7.90 mm。将3种情况共同作用下的误差分布分别与前3种情况进行对比,可以看出其误差分布与检测阵列向上偏移时相近,且在数值上相差较小,表明在各种因素中,检测阵列向上偏移时的影响占据了主要地位,因此在降低安装误差影响的过程中,主要应考虑尽可能限制上下偏移。
3 试验验证
笔者通过实弹射击对理论分析的正确性进行验证,构建了一个有效靶面为 1m×1 m的光幕测试系统,以30 mm弹作为测试对象,相关参数如下:两线激光器之间的水平距离为1 m,光源有效张角为45°,光源高度为2 m,检测阵列长为2 m,线激光器最大功率为1 W,检测阵列的分辨率为1 mm。
在系统完成安装后,以标准安装位置作为基准,将左侧检测阵列依次整体向上平移4 mm,而后以左侧端点为原点向上偏转10′,再以左侧端点为原点向后偏转1°,完成安装误差的人为设置。而为了获取弹丸过靶时的实际坐标,在光幕测试系统前方对应位置安装一张靶面大小为1 m×1 m的纸靶,用于过靶坐标的标定。
通过实弹射击,获得一组测试坐标和标定坐标。对标定坐标进行处理,可以求出当检测阵列存在安装误差时测试系统的理论测试坐标,而后将其与实际测试坐标进行比较,得到了测试坐标与理论坐标的差值。实弹射击各类坐标值如表1所示。

表1 实弹射击各类坐标值 mm
由表1可知,理论坐标与测试坐标并不相等,两者之间存在差值的主要原因是:1)在统计标定坐标时,是以弹孔圆心作为测量点的,而圆心的选择带有主观性,会在确定标定坐标时引入误差,从而使求得的理论坐标存在偏差;2)由于检测阵列测试精度有限,测得的投影坐标不准确,导致最终求出的测试坐标带有误差。尽管理论坐标与测试坐标不相等,但通过分析后发现,上述2个因素对理论坐标和测试坐标造成的影响其实很小,因此理论坐标与测试坐标间的差值并不大,其中x坐标的最大差值为0.88 mm,y坐标的最大差值为1.51 mm。在不考虑误差影响因素的情况下,理论坐标与测试坐标可以近似相等,即理论分析求得的结果与实际情况相符,从而证明了上述误差分析的正确性。
4 结论
笔者以一种双源平行激光光幕系统为研究对象,分析了当单侧检测阵列存在安装误差时对测试结果造成的影响。通过构建坐标误差计算模型,利用MATLAB实现了数值仿真,得出了系统可接受的安装误差范围,分析结果可以作为测试系统安装调整的依据。同时通过对比,确定了系统在安装过程中应尽可能限制检测阵列出现上下偏移。下一步将针对影响测试结果的其他因素进行分析,并以分析结果作为依据,对测试系统进行调整改进,以保证测试结果真实可信。

