基于短时加权峰度的包络解调及其优化研究
樊新海, 张传清, 刘相波, 邱绵浩
(陆军装甲兵学院车辆工程系, 北京 100072)
旋转机械中齿轮、轴承等主要零部件出现故障时常会伴有或强或弱、或持续或断续、或规律明显或随机出现的冲击现象,在实测振动信号中存在冲击成分[1-3]。同时,由于旋转机械内部结构特点,这种冲击成分往往还会和其他频率成分调制在一起。因此,如何从原信号中提取这种冲击成分,并深入分析其频谱结构特点,再结合研究对象的旋转频率、啮合频率、通过频率、固有频率等找到对应信号特征是实现故障辨识和定位的有效手段之一。
基于Hilbert变换的解调方法应用非常广泛,可将原信号中的冲击成分以包络的形式提取出来,且在时域上2次相邻冲击往往间隔时间较长,而在频域上表现为基频较低、倍频衰减较快,因此其能量主要集中在低频段,对此类信号的分析处理通常还需要结合频谱细化技术来共同完成。在稳定工况下,旋转机械振动信号的平稳性较强,零部件故障引起的大幅值冲击脉冲往往间歇性存在,波形样式表现为幅值急速增大后又快速振荡衰减,具有明显的非高斯特性。在存在冲击的时段和不存在冲击的时段,幅域参数有所变化,因此选择合适的幅域参数[4],再结合信号短时处理手段,亦可将其中的大幅值冲击成分有效地提取出来。
鉴于此,笔者利用窗函数截取原信号,以窗口内信号的加权峰度作为幅域参数,再通过窗函数逐点滑动来提取信号中的冲击成分,提出基于短时加权峰度的包络解调方法,并通过与基于Hilbert变换的传统解调方法对比分析,验证该方法的有效性,最后就该方法自身的特点以及窗宽对其解调效果的影响进行深入分析,给出一种基于大幅值冲击成分基频及其倍频功率和占包络总功率比值作为评价指标的最佳窗宽选择方法,实现解调效果的优化。
1 基于Hilbert变换的解调方法
有关信号的包络定义方式并不唯一,而包络提取方法又与定义方式密切相关(即包络定义方式不同,提取方法也不相同),基于Hilbert变换的包络定义方式和提取方法在信号处理领域被广泛应用。
1.1 信号包络的定义
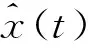

(1)
即x(t)与1/(πt)的卷积。
从线性系统的输入、输出和单位冲激响应函数三者之间的关系来看,Hilbert变换可以看作是x(t)通过一个单位冲激响应为h(t)=1/(πt)滤波器的输出,所以也称之为Hilbert变换器。

(2)
为x(t)的解析信号,并记z(t)的模为
(3)
称为x(t)的瞬时幅值。由于a(t)=|z(t)|≥|x(t)|,因此a(t)是x(t)幅值绝对值的包络,简称包络。
1.2 信号包络的频域算法
由傅里叶变换理论可知:h(t)=1/(πt)的傅里叶变换为H(jΩ)=-jsgn(Ω)。对式(2)两边进行傅里叶变换,有
Z(jΩ)=X(jΩ)+jX(jΩ)H(jΩ)=
(4)
利用式(4)便可得到离散信号x(n)的Hilbert变换及其包络的频域算法,利用离散傅里叶变换及其快速算法来实现。对于N点x(n)(n=0,1,…,N-1),具体算法如下:
1) 计算x(n)的离散傅里叶变换,得到频谱序列X(k)(k=0,1,…,N-1)。
2) 利用X(k)构建Z(k),令
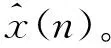
4) 求z(n)的模,即可得到x(n)的包络a(n)。
2 基于短时加权峰度的包络解调方法
2.1 加权峰度
峰度(kurtosis)是随机变量X(t)非高斯性的一种测度[5],定义方式为
Ku1=E(X-EX)4-3[E(X-EX)2]2,
(5)
或
(6)
其中,式(5)是有量纲的,而式(6)是无量纲的。式中:E(X-EX)4为X(t)的4阶中心矩;E(X-EX)2为X(t)的2阶中心矩,亦即方差。
本文在此定义一个新的幅域参数
(7)
式(7)虽然是以比值方式定义,但它是有量纲的,可理解为用方差对峰度Ku2加权,因此称为加权峰度。
2.2 短时加权峰度
短时加权峰度就是将加权峰度与信号短时处理方法相结合[6],用一个窗函数对原信号进行截断,计算窗口内信号的加权峰度(此时的加权峰度是由窗口内的信号计算所得,而与窗口外的信号无关),再通过移动窗重复上述过程,直至信号全部通过窗口。具体算法如下:
1) 对一长离散信号x(l)(l=0,1,…,L-1),利用长度为N′(N′ xm(n′)=x(m+n′)w(n′),n′=0,1,…,N′-1,m=0,1,…,L-N′。 2)xm(n′)的均值和方差分别为 3) 计算xm(n′)的加权峰度 需要注意的是:为了保证短时加权峰度序列的点数与原信号的点数相同,以在时间上不产生延迟错位,且保持窗口内信号原貌,在上述算法中窗函数w(n′)最好选用矩形窗,宽度N′最好是奇数,并先在x(l)数据两端分别补N′/2个0。由于窗函数是逐点滑动的,原信号中的冲击特征会在短时加权峰度中体现出来,且冲击发生的时刻也会相应保留。 图1为某型坦克变速箱被动齿轮断齿时的振动加速度信号,其实车故障模拟测试工况为平坦水泥路、柴油机低速3挡平稳直驶。由图1可以看出:齿轮断齿时,振动信号中明显存在周期性较强的大幅值冲击脉冲。 利用Hilbert变换解调方法对图1所示信号进行处理得到其包络,如图2所示;去除均值后的包络幅值谱如图3所示;频率为0~250 Hz时,利用线性调频Z变换进行25倍频谱细化,得到包络细化谱如图4所示[7]。结合图1-4可以看出:1)原信号中的大幅值冲击特征在其包络中得到了很好的保留和体现;2)大幅值冲击脉冲相邻2次间隔时间较长,其能量主要集中在低频段,而原信号的采样频率较高,因此受频率分辨率的影响,若直接进行频谱分析,往往难以清晰观察到低频段的频谱结构;3)利用频谱细化得到的包络细化谱可清楚观察到大幅值冲击脉冲的基频及其前19阶倍频,而更高阶倍频因衰减和受其他频率成分的影响而变得不明显。 采用窗宽N′=3,99,199的矩形窗函数,分别计算图1所示信号的短时加权峰度,结果如图5所示,对应的细化谱如图6所示。对比图1、5可以看出:短时加权峰度解调方法可将原信号中的大幅值冲击特征提取出来,证明了该方法的有效性,但受窗宽的影响,其又表现出一些自身的变化特点。由图5可以看出:1)当矩形窗较窄时,短时加权峰度具有良好的局部特性,大幅值冲击脉冲被提取出来的同时,小幅值冲击成分也会得到保留,其解调效果更加接近基于Hilbert变换的解调方法,但其优势在于大幅值冲击成分得到了强化突出,频域谐波的规律性更好;2)当矩形窗较宽时,短时加权峰度具有良好的平滑能力,小幅值冲击成分会被抑制,具有低通滤波效果,所得到的包络更为光滑;3)随着窗宽的增加,短时加权峰度在时域上反映信号局部特性的能力减弱,而抑制小幅值冲击的能力增强,所提取包络中单个脉冲的幅值有降低趋势,但脉冲持续时间有增加趋势,脉冲形状有由冲击脉冲先向锯齿脉冲转变,再向矩形脉冲转变趋势。 由图6可以看出:在频域上,周期性脉冲的基频对应的幅值有增大趋势,而倍频对应的幅值随谐波阶次的增加整体上有加快衰减趋势。 通过上述分析可以看出:1)基于Hilbert变换的解调方法的包络定义明确,对整个信号解调得到的包络完全由信号自身决定,不受其他因素影响;2)基于短时加权峰度的解调方法得到的包络并没有严格的定义,又因窗的存在致使所提取的包络不仅与信号自身有关,还会受窗宽的影响,也就是说,即使是同一信号,不同窗宽解调得到的包络形状也不同。 利用短时加权峰度提取信号中的大幅值冲击成分时,窗函数的宽度选择非常重要,但也很难给出窗宽选择的公认准则。总体来看,窄时窗反映局部性能好,宽时窗平滑能力强:若原信号中的冲击脉冲持续时间短,想保留冲击脉冲中的细节,应采用窄时窗;若原信号中的冲击脉冲持续时间较长,重点观察脉冲整体变化趋势,应采用宽时窗。因此,需要就窗宽问题给出一种优化选择方法。 原信号中大幅值冲击成分是需提取保留的,但短时加权峰度解调得到的包络中难免还会保留一些其他成分。由于大幅值周期性冲击成分在频域具有很强的谐波性,能量主要集中在基频及其倍频处,因此,可用包络细化谱中基频及其倍频的功率和占包络总功率的比值作为评价指标,来量化所提取包络的质量,通过窗宽与评价指标之间的关系来确定最佳窗宽。具体方法如下: 2) 用给定的窗宽N′对原信号进行基于短时加权峰度的解调,得到包络a(l),其总功率 对比图2、8可以看出:基于短时加权峰度优化解调得到的包络,既突出保留了大幅值冲击脉冲,同时又很好地抑制了小幅值冲击成分,包络整体较为光滑,单个大幅值冲击脉冲持续时间也基本与图1中相同。 对比图4、9可以看出:图9中前12次谐波频率成分清晰可见,谐波幅值随谐波阶次基本呈线性降低趋势,规律性明显优于图4,且频段内包含其他频率成分少,细化谱也更为干净。 针对机械振动信号中大幅值冲击成分提取和分析问题,提出了基于短时加权峰度的解调方法,与基于Hilbert变换的传统解调方法进行了对比分析,结果表明: 1) 当窗宽较窄时,短时加权峰度的解调效果较接近基于Hilbert变换的解调方法,但前者对大幅值冲击脉冲有强化作用,由于窗宽的改变增加了其应用的灵活性,使用不同的窗宽可以得到不同的解调效果。 2) 当使用窄时窗时,短时加权峰度解调效果反映信号的局部性能好;宽时窗平滑能力强,会起到一定的低通滤波作用,抑制小幅值冲击成分。 3) 采用包络细化谱中大幅值冲击成分的基频及其倍频功率和占包络总功率的比值作为评价指标,可实现最佳窗宽选择和基于短时加权峰度的优化解调。
3 解调效果的对比分析
4 窗宽的优化选择
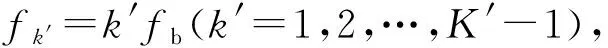
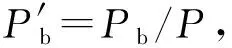
5 结论

