非理想状态下斜幕面对四光幕阵列精度靶测量误差的影响*

陈 瑞，倪晋平，马时亮

(西安工业大学 陕西省光电测试与仪器技术重点实验室，西安 710021)

弹丸密集度一直是衡量枪、炮和弹药性能的一项重要参数[1-2].传统的密集度测量，多采用接触式方法，此方法无法实现实时测量，且具有一定的危险性.近些年国内外研究了多种不同的非接触式测量方法[3-7]，其中，利用天幕靶光幕[8]或光幕靶光幕[9]构成的四光幕阵列精度靶，以其结构简单，使用维护方便及成本低等优点，在国内外靶场得到广泛应用[10-12].四光幕阵列精度靶在空间形成特定形式排列的四光幕结构[13]，根据选定的空间直角坐标系，分别定义三个基准面为水平面(XOZ平面)、铅垂面1(XOY平面)和铅垂面2(ZOY平面)，将四个光幕看作平面[14]， 则光幕Ⅰ和光幕Ⅳ沿预设弹道的垂直方向放置并与铅垂面2平行，光幕Ⅱ、光幕Ⅲ在光幕Ⅰ与光幕Ⅳ之间交错倾斜放置，本文统称为斜幕面.且光幕Ⅱ严格垂直于水平面、光幕Ⅲ严格垂直于铅垂面1，此时光幕Ⅱ与光幕Ⅲ与基准面的结构关系属于理想状态.文献[14]对四光幕阵列精度靶测量误差的分析均是基于此类理想状态.而在工程实现中，光幕Ⅱ与水平面、光幕Ⅲ与铅垂面1之间的垂直关系往往难以保证，不是严格的90°，本文称之为斜幕面的非理想状态.当两个斜幕面处于非理想状态时，势必会带来光幕阵列空间结构的改变，从而带来测量误差.本文建立斜幕面非理想状态下的四光幕阵列测量模型，推导误差传递公式，并通过MATLAB分析弹丸入射坐标、斜幕面位置及斜幕面与基准面倾角等因素对四光幕阵列精度靶测量误差的影响，为工程实际测量提供参考.

1 测量原理

图1为四光幕阵列精度靶的理想结构模型[13]，建立以光幕Ⅰ中心为原点的三维直角坐标系，其在XOZ和XOY平面上的投影视图分别如图2(a)和图2(b)所示，其中α表示光幕Ⅱ与YOZ平面的夹角，β表示光幕Ⅲ与YOZ平面的夹角，S为光幕Ⅰ与光幕Ⅳ之间的距离.四个探测区域为矩形的光幕以特定的角度布置在六面体中，预设弹道O1O2与光幕Ⅰ垂直，T1、T2、T3、T4依次为弹丸穿过四个光幕时与光幕的交点.α、β、S统称为光幕阵列的结构参数.

若测时仪记录下弹丸在T1、T2、T3、T4的时刻信息分别为t1、t2、t3、t4，则弹丸穿过光幕Ⅰ和光幕Ⅳ的平均速度v可以表示为

v=S/t4

(1)

弹丸在平行于YOZ平面的靶面内的着靶坐标(z、y)为

(2)

(3)

图1 四光幕阵列理想模型

图2 理想模型投影视图

式(2)和式(3)分别表示四光幕阵列精度靶对弹丸横坐标z和纵坐标y的测量结果，可以看出，弹丸着靶横坐标测量结果仅由S、α、t1、t2和t4决定，即其仅与光幕Ⅰ、光幕Ⅳ和光幕Ⅱ相关；而弹丸着靶纵坐标测量结果仅由S、β、t1、t3和t4决定，即其仅与光幕Ⅰ、光幕Ⅳ和光幕Ⅲ相关.因此，在分析非理想状态下斜幕面对四光幕阵列精度靶着靶坐标测量误差的影响过程中，需分析光幕Ⅱ倾斜对弹丸着靶横坐标z的测量误差影响和光幕Ⅲ倾斜对弹丸着靶纵坐标y的测量误差影响.

2 误差分析

2.1 理想状态误差分析

理想状态下光幕Ⅱ在XOZ面内的投影为一条线段，测量误差主要受结构参数误差(dS、dα、dβ)、测时误差(dt1、dt2、dt3、dt4)以及弹丸入射位置(z，y)等因素影响[15].为了分析误差最大值，本文参考工程实际，选取结构参数S=1 m、α=β=30°，装调误差dS=0.5 mm、dα=dβ=0.02°，测时仪测时误差dt1=dt2=dt3=dt4=0.1 μs，弹丸速度V=800 m·s-1，计算光幕面Ⅰ内以坐标系原点为中心，1 m×1 m矩形靶面范围横坐标测量误差分布，得到其最大值约为0.9 mm.

2.2 非理想状态误差分析

首先分析非理想状态下斜光幕Ⅱ与XOZ面不垂直的情况，其光幕如图3所示.图3中Y′轴与Z′轴分别为Y轴与Z轴沿X轴的平移，平移后的原点O′仍然在X轴上，光幕Ⅱ与Y轴的夹角γ表示幕面Ⅱ与XOZ面的倾斜程度，幕面Ⅱ与Y轴交点I的纵坐标为h，则光幕Ⅱ在XOZ面内的投影如图4所示.

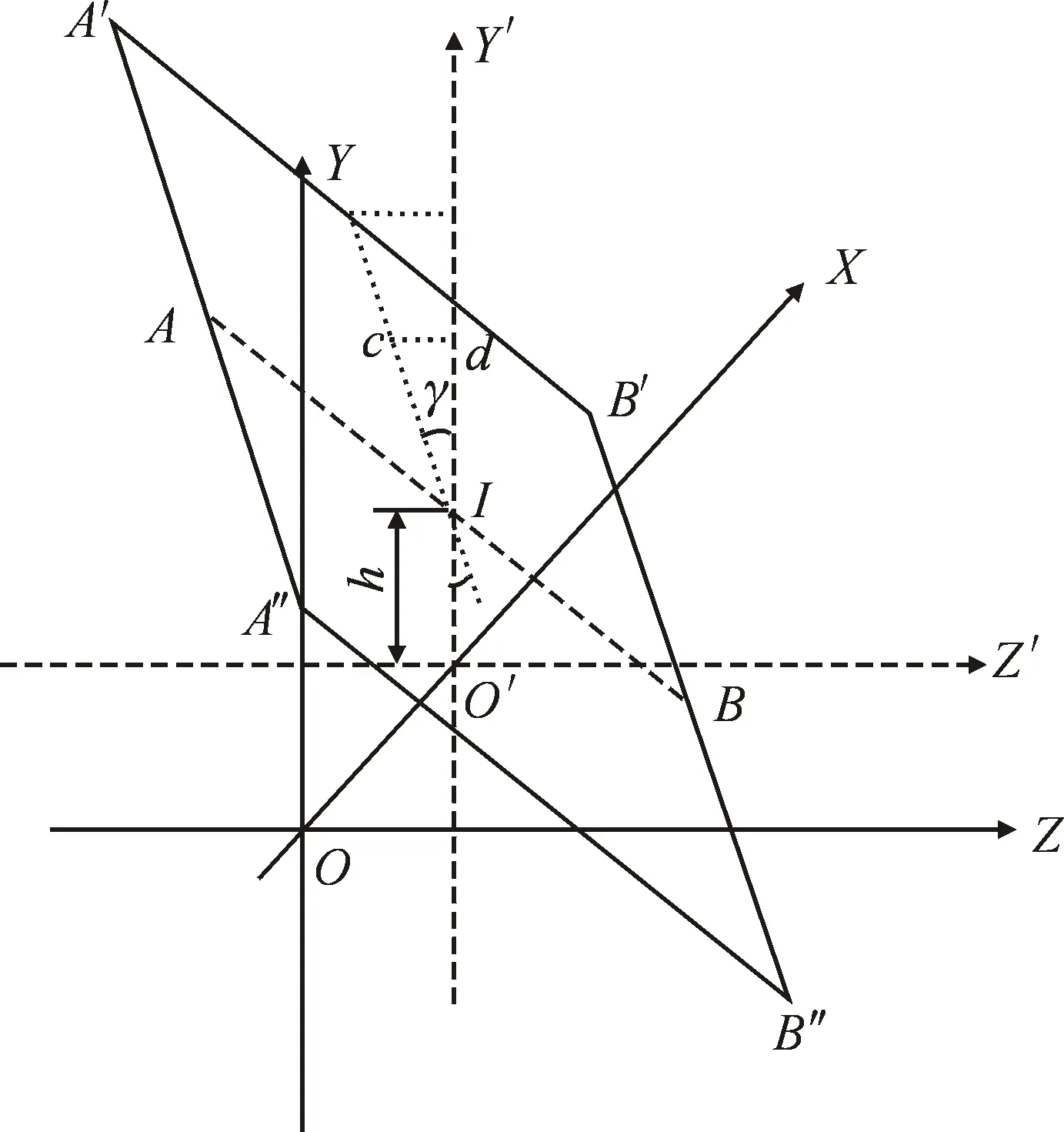
图3 不垂直于XOZ面的光幕Ⅱ

图4 非理想状态下的XOZ面投影图

平行四边形A′A″B″B′表示光幕Ⅱ在平面XOZ内的投影，A′B′和A″B″分别为光幕Ⅱ上边界和下边界投影，AB为光幕面Ⅱ内平行于XOZ面且过I点线段的投影，与图2(a)中光幕Ⅱ投影位置重合，图4中因其并非实际存在，用虚线表示.不同高度下光幕Ⅱ的投影为一系列平行线，因这些平行线在XOZ平面内沿弹道方向分开了一定的距离，导致弹丸到达光幕Ⅱ的时刻产生偏差，即式(2)中t2产生了Δt2的变化量，从而给测量带来误差.

对于一发确定的弹丸，其与光幕Ⅱ交于确定位置，光幕Ⅱ内平行于XOZ面且过弹丸与光幕Ⅱ交点的线段投影可以表示为mn，其与AB之间的距离用cd表示为

cd=(y-h)×tan(γ)

(4)

其中y为弹丸入射纵坐标，mn与AB沿弹道方向分开的距离为ed.

(5)

弹丸过光幕Ⅱ的时刻变动为

(6)

故光幕Ⅱ倾斜引起的横坐标测量误差为

(7)

用类似的方法分析非理想状态下斜光幕Ⅲ与XOY面不垂直的情况，光幕Ⅲ与Z轴的夹角θ表示幕面Ⅲ与XOY面的倾斜程度，幕面Ⅲ与Z轴交点的横坐标为k，可以得到光幕Ⅲ倾斜引起的纵坐标测量误差为

(8)

3 非理想状态误差仿真

由式(7)可知，非理想状态四光幕阵列精度靶横坐标测量误差直接受到弹丸入射纵坐标(y)、光幕Ⅱ与Y轴交点位置(h)以及光幕Ⅱ倾斜的角度(γ)的影响；由式(8)可知，非理想状态四光幕阵列精度靶纵坐标测量误差直接受到弹丸入射横坐标(z)、光幕Ⅲ与Z轴交点位置k以及光幕Ⅲ倾斜的角度(θ)的影响.通过仿真分析测量误差与上述各因素之间的关系.

3.1 入射位置对测量误差的影响

首先考虑光幕Ⅱ与Y轴交点位于Y轴原点这一简单情况，即式(7)中h=0 mm，取2.1节中的参数不变，S=1 m、α=β=30°，弹丸速度V=800 m·s-1，依次在光幕Ⅱ倾角分别为γ=0.03°、γ=0.05°、γ=0.08°、γ=0.1°四种情况下，仿真分析坐标系原点为中心1 m×1 m矩形靶面范围内的横坐标测量误差，结果如图5所示.

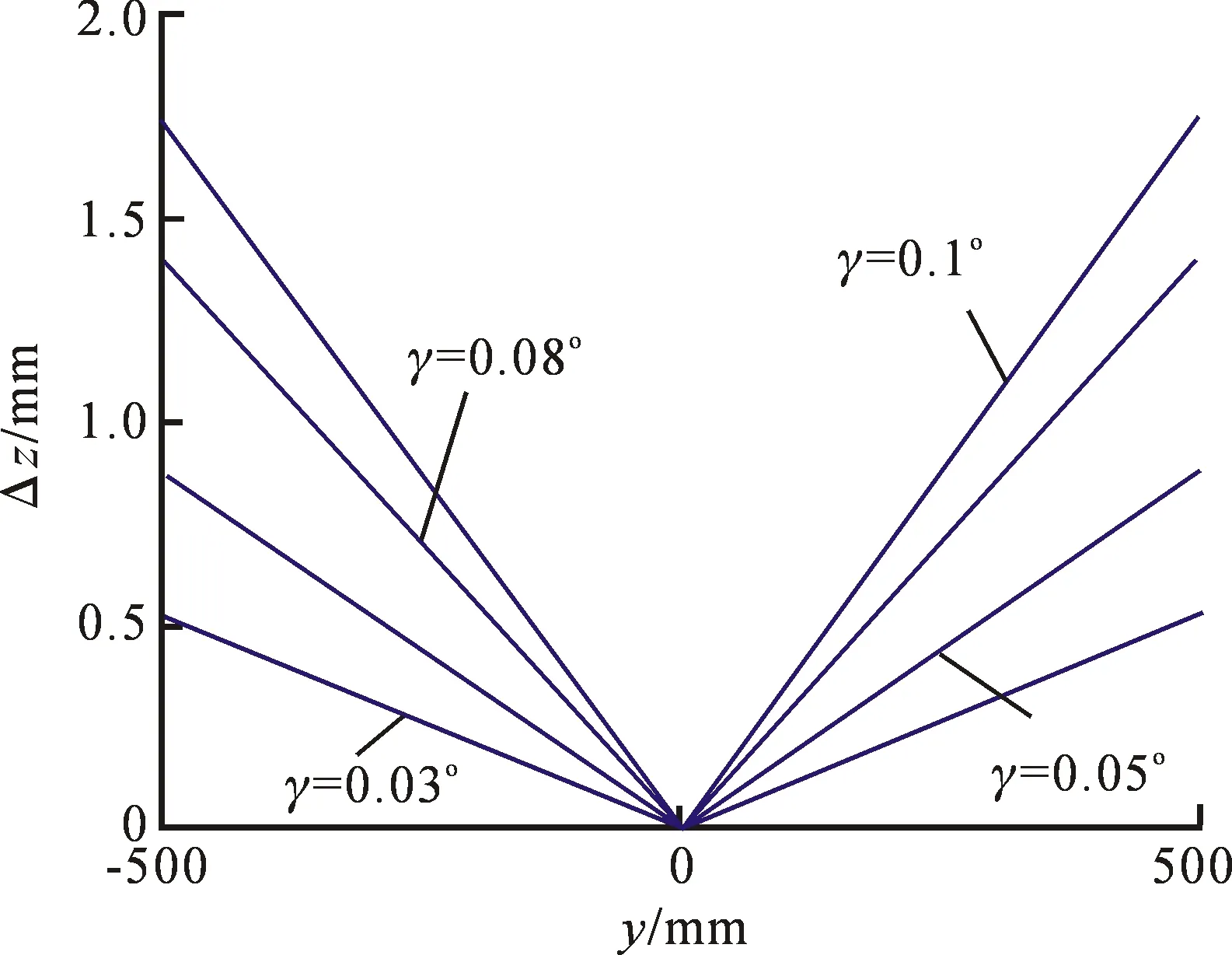
图5 入射位置与测量误差关系

图5中横坐标表示弹丸入射纵坐标(y)，纵坐标表示弹丸着靶横坐标测量误差(Δz)，由图5可看出，在上述仿真条件以及光幕Ⅱ倾角γ取值不同的情况下，横坐标测量误差受弹丸入射纵坐标影响的变化趋势一致，关于y=0 mm位置均呈“V形”对称分布，弹丸入射纵坐标绝对值越大的地方误差越大，最终在靶面上、下边沿处误差达到极大值.

考虑光幕Ⅲ与Z轴交点位于Z轴原点即式(8)中k=0 mm，在光幕Ⅲ倾角θ=0.03°、θ=0.05°、θ=0.08°和θ=0.1°四种情况下，仿真分析坐标系原点为中心1 m×1 m矩形靶面范围内的纵坐标测量误差，可以得到与光幕Ⅱ一致的结论，即光幕Ⅲ倾角θ取值不同的情况下，纵坐标测量误差关于z=0 mm位置均呈“V形”对称分布，弹丸入射纵坐标绝对值越大的地方误差越大，最终在靶面左、右边沿处误差达到极大值.

3.2 斜光幕位置对测量误差的影响

由于光幕Ⅱ发生倾斜时，误差极大值出现在靶面上(或下)边沿位置，取各参数不变，斜光幕Ⅱ与Y轴夹角固定为γ=0.03°，分析斜光幕Ⅱ与Y轴交点对测量误差的影响，即使h取值从-500 mm逐渐增加至500 mm，仿真分析靶面上边沿 (y=500 mm) 处误差分布如图6所示.

图6中横坐标表示光幕Ⅱ与Y轴交点位置(h)，纵坐标表示弹丸横坐标测量误差(Δz)，当交点位于Y轴最下端时，靶面上边沿测量误差有极大值，约为1.05 mm，随着交点向Y轴正向移动，误差逐渐减小，当交点I移动至靶面上边沿时，光幕Ⅱ倾斜角度γ带来的测量误差趋近于零，结合图5可以分析得到，在弹丸入射位置距离光幕Ⅱ与Y轴交点越远的地方误差越大.

图6 斜光幕位置与测量误差的关系

用类似的方法对光幕Ⅲ发生倾斜的情况进行分析，可以得到与光幕Ⅱ类似的结论，即在弹丸入射横坐标距离光幕Ⅲ与Z轴交点越远的地方误差越大，误差极大值约为1.05 mm.

3.3 斜光幕倾斜角对坐标测量误差的影响

为了更好的指导工程实际需对测量误差最大值进行分析，取其他参数不变，光幕Ⅱ与Y轴交点选定在Y轴最下端(h=-500 mm)，令γ由-0.1°逐渐增大至0.1°，对靶面上边沿(y=500 mm)位置的测量误差进行仿真，得到非理想状态下光幕倾斜角度给四光幕阵列精度靶带来的测量误差最大值Δzmax与γ的关系，如图7所示.

图7 测量误差最大值随斜光幕倾角的分布

图7中横坐标γ取负值表示光幕Ⅱ倾向Y轴的另一侧，其误差分布与γ取正值时对称，即横坐标测量误差最大值(Δzmax)与光幕Ⅱ的倾斜方向无关.考虑γ为正的情况，误差随γ的增大而增大，当γ增至0.1°时光幕Ⅱ倾斜角度γ带来的误差最大值约为3.5 mm.

取其他参数不变，分析非理想状态下光幕Ⅲ倾斜角度θ对纵坐标测量误差最大值的影响进行分析，可以得到与光幕Ⅱ一致的结论，即纵坐标测量误差最大值(Δymax)与光幕Ⅲ的倾斜方向无关，考虑θ为正的情况，误差随θ的增大而增大，当θ增至0.1°时光幕Ⅲ倾斜角度θ带来的误差最大值约为3.5 mm.

在工程实际中，四光幕阵列精度靶的测量误差受理想状态下误差和非理想状态下误差的共同影响，且两种情况下的误差不相关.为了对误差进行限制，综合考虑理想状态下误差与非理想状态下的误差最大值，通过计算可以得到，若要使四光幕阵列精度靶误差最大值Δzmax及Δymax限制在2 mm以内，需限制斜光幕Ⅱ及光幕Ⅲ的倾斜角γ及θ均不大于0.03°.

4 结 论

本文通过构建斜光幕与坐标系基准面不垂直的非理想状态模型，对四光幕阵列精度靶测量误差进行了分析，通过仿真得到该模型下各因素与测量误差的关系为

1) 光幕倾斜对坐标测量带来的误差，受弹丸入射位置坐标影响，且在入射坐标绝对值越大的地方误差越大，误差的极大值出现在靶面边沿位置；

2) 靶面边沿处的误差随倾斜光幕与坐标轴交点的远离而增大，当交点移至远处的靶面边沿时，出现误差极大值；

3) 在γ由-0.1°变化至0.1°的过程中，测量误差关于γ=0°对称，且均随γ绝对值的增大而增大，即测量误差与光幕的倾斜方向与误差无关，当γ=0.1°时，非理想状态下的横、纵坐标测量误差最大值约为3.5 mm；

4) 综合考虑理想状态和非理想状态下的情况，为使工程实际中四光幕阵列精度靶测量误差不大于2 mm，需限制光幕Ⅱ和光幕Ⅲ的倾斜角均不大于0.03°.