基于分段趋势分析的复合材料弹道侵彻模型诊断
宫 雷, 许世蒙
(陆军装甲兵学院基础部, 北京 100072)
弹道侵彻的数值模拟综合利用流体力学、温度场、电传导、磁场等领域的相关理论,将计算机软件、数学算法与弹道侵彻机理相结合,成功地解决了该领域的实际问题,具有广泛的应用价值,是3维编织复合材料的弹道侵彻研究的重要方法之一[1-2]。
数值模拟过程中,模型诊断是必不可少的环节[3-5],传统的模型诊断方法[6-7]基于残差分析,通过拟合优度检验和F检验,对数值模拟与试验结果的剩余速度在同一模型下残差的分布进行同一性检验。其中:拟合优度检验通过决定系数判断回归方程对样本数据的拟合程度;F检验对模型中回归变量与响应变量之间的线性关系是否显著成立进行判断。这些方法在一定程度上是有效的,但其条件要求较高,计算也较复杂。笔者以试验结果为基础,在模型诊断中采用分段趋势分析,该方法操作简单、行之有效,较好地弥补了传统模型诊断方法的上述不足。
1 试验与数值
1.1 试验材料及方法
靶板制备[8]时,纤维材料采用荷兰Tarpon 1000型对位芳族聚酞胺纤维长丝束,基体使用热固性环氧树脂,采用四步法1×1纵横阵列编织机进行织造。
采用56式弹道发射枪,质量为7.95 g的7.62 mm步枪标准弹,HG202A-Ⅱ型电子测试仪,用2组锡箔作计时触发器测试子弹的入射速度和剩余速度。
1.2 数值模拟主要指标
3维编织复合材料的动态侵彻数值模拟采用LS-DYNA程序,采用变时步长增量解法进行了2组有限元模拟,其中:材料模型均采用塑性动力学材料本构模型;准细观精细模型中,弹体、树脂和纤维束的单元类型均采用八节点六面体实体单元。2组有限元模拟方法的主要不同指标如表1所示。

表1 2组有限元模拟方法的主要不同指标
1.3 结果
3维编织复合材料弹道侵彻试验结果与模拟结果如表2所示。
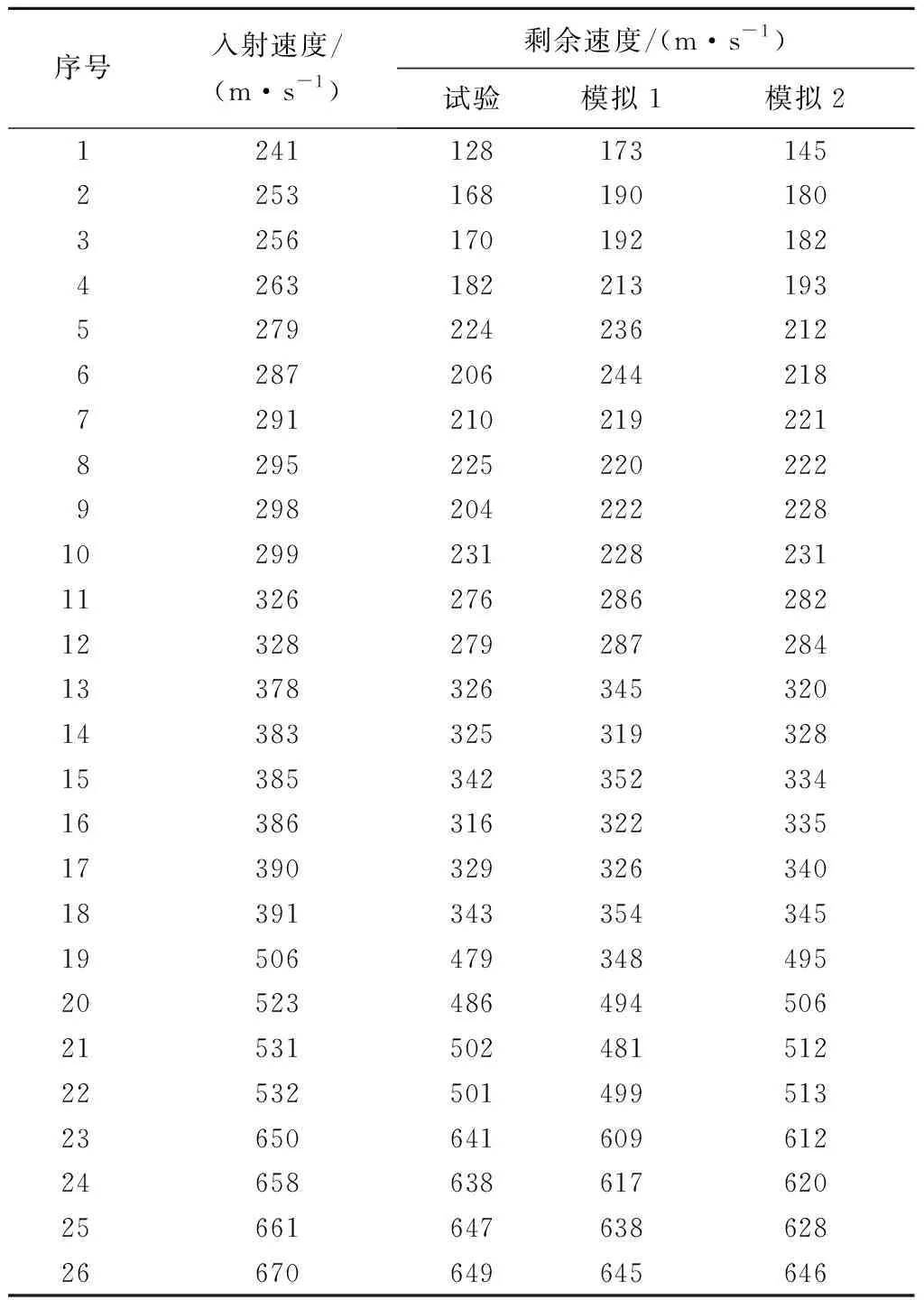
表2 3维编织复合材料弹道侵彻试验结果与模拟结果
2 回归模型诊断
在3维编织复合材料弹道侵彻试验和数值模拟的对比分析中,检验剩余速度和入射速度的线性关系是否相同。
令x表示入射速度,y表示试验中剩余速度,应用最小二乘法回归,可以得到剩余速度与入射速度的关系:
y=1.171 3x-124.020 7。
(1)
2.1 残差分析
将回归模型(1)分别应用于试验数据和2组有限元模拟数据中的剩余速度与入射速度,得到的残差如图1所示。
由图1可以看出:模拟数据1的残差明显具有增加的趋势,模拟数据2的残差大都小于0,初步可认为回归模型(1)不适合2组有限元模拟数据。
2.2 拟合优度检验与F检验
对试验数据和2组模拟数据的回归模型进行拟合优度检验和F检验,其结果如表3所示。可以看出:1)2组模拟数据回归模型的拟合优度检验决定系数R2>0.95,说明拟合优度较大,响应变量对回归变量的解释程度较高;2)F检验中的p值均小于0.01,说明总体上响应变量与回归变量之间的线性关系显著。

表3 回归模型检验结果表
上述结果表明:回归模型(1)能够较好地解释试验和数值模拟的入射速度与剩余速度的关系,且试验和数值模拟结果一致。
2.3 传统检验方法的不足
结合图1和表3可知:拟合优度检验与F检验的检验结果一致,但与残差图结果相矛盾。进一步分析拟合优度检验和F检验可得到以下结论:
1) 拟合优度检验中的决定系数R2仅能说明列入模型的所有解释变量对因变量的联合影响程度,但对存在局部系统误差的模型反应不灵敏,不能说明哪些样本点不适合此模型。
2)F检验的理论基础是基于正态分布,若模型检验中使用F检验,残差需服从正态分布。
试验数据、模拟数据1和模拟数据2在回归模型(1)的残差直方图如图2所示。可以看出:在回归模型(1)下,试验数据的残差具有正态分布特征,而模拟数据1的残差则不具有正态分布特征,模拟数据2的残差具有厚尾特征。采用Kolmogorov检验对试验数据、模拟数据1和模拟数据2进行正态检验,得到的p值分别为0.025、0.575、0.817 5,说明试验数据的残差服从正态分布,可进行F检验;模拟数据1和模拟数据2的残差不服从正态分布,不可进行F检验。
3 分段趋势诊断方法
趋势性分析直观上较容易理解,并不需要太多的数学和统计理论,将其引入到模型检验中,可有效检验模型的有效性。
3.1 分段趋势统计量的构造
检验假设:
H0:任意2组残差无上升或下降趋势。
H1:存在2组残差有上升或下降趋势。
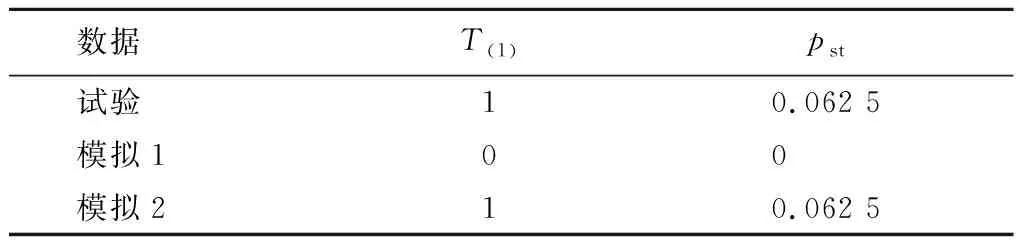
令{ε1,ε2,…,εn}表示残差数据集,n0表示每组相互比较的数据集中的元素个数,取数对集 {(εi,εi+c),(εi+1,εi+1+c), …,(εi+n0-1,εi+n0+c-1)},其中i=1,2,…,n-c,0 构造分段趋势统计量: (2) (3) pst=P{T(1)≤t(1)}。 (4) 式中:t(1)为T(1)的观察值。Tm能够检验任意2组残差是否存在上升或下降趋势,T(1)与pst均能检验模型是否存在局部系统误差:当模型局部系统误差不存在时,T(1)的值接近组中元素个数的1/2,此时模型拟合程度越好;pst为模型不存在系统误差的概率。 定理1:连续型随机变量X1、X2相互独立且具有相同的分布,其密度函数均为f(x),则P{X1≥X2}=P{X1≤X2}=1/2。 证明:由于X1、X2相互独立,由卷积公式可得X1-X2的密度函数 (*) 令x+z=u,则有x=u-z,这时式(*)可改写为 fX1-X2(z), 说明X1-X2的密度函数关于z轴对称。有 P{X1≥X2}=P{X1≤X2}=1/2。 证毕。 (5) 表4为根据式(5)计算的不同元素个数n0下pst的值。可以看出:取显著性水平α=0.05,当t=0,n0=6时,pst=0.016<α,说明当n0过小时,趋势检验不够灵敏,实际应用中应使n0>6。 分段趋势诊断过程中,需依据试验条件和数据量选择n0,然后依次计算Tm、T(1)与pst的值。当显著性水平为α时,若pst≤α,说明残差具有上升或下降趋势,需重新调整模型;若pst>α,说明残差无上升或下降趋势,回归模型能够解释回归变量与响应变量的关系。 表4 不同元素个数n0下pst的值 为保证分段趋势检验的灵敏度,令组中元素个数n0=7,依据分段趋势统计量的构造方法,比较每组7对残差的大小关系并计算T(1)和pst的值,如表5所示。 表5 分段趋势诊断表 由表5可以看出:取显著性水平α=0.05,模拟数据1中分段趋势统计量T(1)=0,pst=0<α,试验数据和模拟数据2中分段趋势统计量T(1)=1,pst=0.062 5>α,说明模拟数据1没有通过分段趋势检验,残差局部存在增加或减少的趋势,而试验数据和模拟数据2通过了检验。 分段趋势诊断方法能诊断出模型中的局部系统误差,可更好地区分模型对数据的不合理解释;分段趋势诊断方法本质上是非参数方法,没有参数方法中残差的正态假设或渐进正态假设,更具普适性;在3维编织复合材料弹道侵彻试验与数值模拟结果的对比分析中引入分段趋势分析方法,能够更有效地诊断试验与数值模拟结果对回归模型的同一性。3.2 分段趋势统计量的分布律





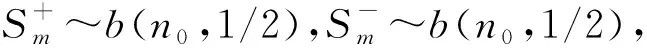
3.3 n0对检验的影响

4 分段趋势诊断
5 结论
——拟合优度检验与SAS实现

