基于LCD与双谱分析的齿轮故障特征提取

仝 蕊， 康建设， 李宝晨， 钟 文

(1. 陆军工程大学石家庄校区装备指挥与管理系， 河北 石家庄 050003；2. 陆军工程大学科研学术处，江苏 南京 210007； 3. 95685部队 云南 昆明 650000)

振动信号处理和特征提取是齿轮故障诊断及预测的核心问题，有效的特征提取方法对提高齿轮箱故障预测准确程度具有重要意义[1]。齿轮振动信号通常表现出复杂的时变特性，尤其是故障信号具有非平稳和非高斯分布的特征。谱分析方法是处理非高斯信号的有效方法，能够有效提取振动信号特征，被广泛应用于机械设备的信号处理中。

目前，常用的谱分析方法主要有功率谱分析、倒谱分析、奇异谱分析和高阶谱分析等方法。其中：功率谱分析方法采用时域统计指标、功率谱密度分析信号的频域结构，其对非线性较强的信号处理效果不佳[2]；倒谱分析方法是在对功率谱取对数的基础上进行谱分析，在放大特征分量的同时也放大了噪声和其他分量信息，因此影响了特征提取效果[3]；奇异谱分析方法是基于二阶统计的协方差矩阵进行谱分析，但分析非线性信号效果不理想[4]；双谱分析方法是一种典型的高阶谱分析方法，它既可以消除非线性信号中高斯干扰成分，同时又保留了其中的非高斯成分，适于处理具有周期性和调制性的齿轮振动信号[5]。但双谱分析方法从理论上仅能抑制高斯噪声，而对非高斯噪声无能为力，且直接对信号整体进行分析，无法剔除谐波及其他不必要分量信号的干扰。

通过局部特征尺度分解(Local Characteristic-scale Decomposition，LCD)[6]可提取双谱分析所需的包含敏感信息的信号分量，其在迭代速度和分解能力等方面具有明显优势，但对内禀尺度分量(Intrinsic Scale Component,ISC)的筛选并无一套系统科学的方法。为弥补上述缺陷，笔者提出一种利用LCD分解和双谱分析相结合的故障特征提取方法,其先对LCD算法进行优化，筛选有用分量，再结合双谱分析计算出双谱熵(Bispectral Entropy,BIE)作为故障特征量，最后通过齿轮预置故障试验对该方法进行验证。

1 局部特征尺度分解的优化

1.1 LCD算法

利用LCD对任意一个复杂的振动信号x(t)进行分解[7]，分解为有限个不同ISC分量之和，且任意2个ISC分量相互独立，其计算步骤如下：

1)选择合适参数构造高频谐波信号H(t)，进行并叠加：

H(t)=Ucos(2πft)，

(1)

x′(t)=x(t)+H(t)。

(2)

式中：U为幅值，常取U=max(x(t))；f为频率，常取f=fs/2[7],其中fs为采样频率。

2) 确定x′(t)的极值点Xk′(k′=1,2,…,M)及对应时刻τk′，其中M为极值点数。

3) 计算Xk′的函数值

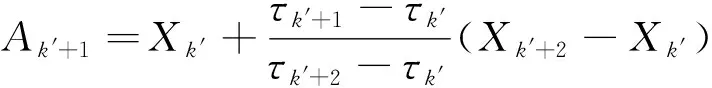
(3)

在任意2个极值点之间对x′(t)进行线性变换,可得

Lk′=aAk′+(1-a)Xk′,k′=2,3,…,M-1。

(4)

式中：a=0.5[6]。通过延拓获得左右端点值，具体方法为[7]：在左端增加一个极值点进行左延拓，即令X0=X2，τ0=2τ1-τ2，由式(4)可得到L1；同理，在右端点增加一个极值点进行右延拓，即令XM+1=XM-1，τM+1=2τM-τM-1，由式(4)可得到LM。利用式(4)计算A1和AM。

4) 利用三次样条函数[7]对L1，L2，…，LM进行拟合，对得到的基线B1(t)分离

h1(t)=x(t)-B1(t),

(5)

判断h1(t)是否满足ISC分量条件[8]：若满足，则输出ISC1=h1(t)；否则，以h1(t)作为原始数据，重复步骤1)-4)，直到得到ISC分量。

5) 从原始数据中分离ISC1分量，将剩余信号作为新的原始数据u1(t)，重复步骤2)-4)，直到提取ISC分量n′次后满足un′(t)为单调函数或为常函数为止，最终得到ISC1，ISC2，…，ISCn′及趋势项un′(t)。

1.2 ISC分量的筛选

分析振动信号的LCD分解过程发现：原始信号所包含的故障信息被细化到各个分量信号中，产生了包含关键故障信息的ISC分量。分量信号不仅含有较多的故障特征信息，还含有较多的干扰信息。为了减少干扰分量的影响，对LCD算法进行优化，并选择合适的方法对分解出的ISC分量进行筛选，具体方法如下：

1) ISC分量个数m的估计。将LCD分解所得的ISC分量和趋势项un′(t)与分解前的原始振动信号x(t)进行重组，构成新信号xob(t)={x(t),ISC1(t),…,ISCn′(t),un′(t)} 。构建xob(t)的相关矩阵R，并进行奇异值分解[8]：

(6)

式中：u′为xob(t)的维数；Λd为包含d个主特征值的主特征值矩阵；Vd为奇异值矩阵；Λu′-d为包含u′-d个噪声特征值的噪声特征值矩阵。Λu′-d的噪声特征值理论上与噪声功率相等，且取值非常小，故可根据矩阵R中最小特征值的个数直接确定主特征值数，估算出m值。但实际应用中，噪声大小并不能控制和估算，尤其是在强噪声背景下无法有效确定出主特征值与噪声特征值间的阈值。因此，本文以R的奇异值分解结果中的非零特征值为参考，结合贝叶斯信息准则(Bayesian Information Criterion,BIC)[7,9]

(7)

2) 有用ISC分量的确定。峭度可有效体现信号中的冲击特征，为了提取有用的ISC分量，可将计算的ISC分量和原始信号的峭度时间序列互相关系数作为筛选有用ISC分量的评判指标。对采样长度为N的原始信号x(t)，因需要足够多的样本计算才有意义，故选择计算峭度时的长度a′=30。以xi(i=1,2,…,N-a′+1)为起点，从原始振动信号中依次向后截取长度为a′的数据序列[10]，计算其峭度值，从而得到长度为N-a′+1的峭度时间序列K(i)：

(8)

,

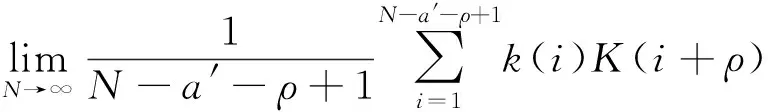
(9)

式中：ρ为互相关函数取得最大值的间隔数。

互相关系数的大小反映了不同ISC分量与原始信号之间的相关性。信号经过LCD分解后，各有用分量与原始信号的相关性约等于该分量的自相关；而非有用分量与原始信号的相关性很小[12]。互相关系数越大，包含的敏感信息越多；反之，干扰成分越多。因此，结合前面估计的m个ISC分量，选取互相关系数最大的前m个ISC分量作为有用分量，即为后续双谱分析融合的信号分量。

2 双谱分析

2.1 双谱估计

双谱定义为三阶累积量的二维离散傅里叶变换，用Bx(ω1,ω2)表示，其表达式可参考文献[13]。由于高斯平稳随机信号的三阶累积量为0，其双谱值也为0，因此理论上双谱分析能消除信号中的高斯噪声干扰，同时将信号中的非高斯成分保留。由于所采集的齿轮振动信号为一定长度的离散序列，无法准确计算双谱值，因此可采用基于傅里叶变换的非参数化估计方法进行双谱估计。具体方法如下[14]：

1) 将采样长度为N的输入信号x(t)分成X段，每段W个数据点，并将每段数据去均值处理。

2) 计算第j(j=1,2,…,X)段数据xj(t)(t=0,1,…,W-1)的离散傅里叶变换系数

(10)

式中：η=0,1,…,W/2，为离散傅里叶变换后各数据点对应的编号。

3) 计算各段数据的三重相关

Y(j)(η2+X2)Y(j)(-η1-X1-η2-X2),

(11)

式中：Δ0=fs/N0，为所要求的频率样本间隔，其中N0为样本数；η1+η2≤fs/2，0≤η2≤η1,其中η1、η2分别为任2段信号数据X1、X2离散傅里叶变换后对应编号；W=(2L1+1)N0。

4) 计算双谱估计值

(12)

2.2 双谱熵的计算

2) 计算定义域频域内所有点的双谱幅值概率

(13)

3) 计算双谱熵值

(14)

由于BIE包含了对有用ISC分量信息的融合处理，因此其对频带能量的变化更为敏感：故障程度越轻时，其能量在各频带分布较均匀，对应BIE值越大；故障程度越重时，其能量主要集中在少数一些特征频带上，对应BIE值越小。在此，将经LCD分解获得ISC分量，然后利用双谱分析得到的BIE作为故障特征量，称为LCD-BIE,上述特征提取过程称为LCD-BIE特征提取方法。

3 试验分析验证

3.1 齿轮故障特征的提取

为验证LCD-BIE特征提取方法的实用性，将该方法应用于齿轮预置故障试验的实测振动信号中。以齿轮正常状态、裂纹故障、断齿故障为例。试验台包括二级平行轴变速箱、4 kW三相电磁调速电动机、风冷磁粉制动器各1个，还包括1套数据采集系统、1台计算机、4个3056B4型压电加速度传感器、PXI-1031机箱、数据采集卡及LabVIEW软件。该变速箱齿轮的齿数分别为：高速轴齿轮35个齿；中间轴大齿轮64个齿；中间轴小齿轮19个齿；低速轴齿轮81个齿。在齿轮箱壳体安装传感器，采集齿轮箱振动信号。试验负载为10 N·m，转速为800 r/min，采样频率为20 kHz，采样时间为6 s。

在输出轴大齿轮齿根上以线切割角度α进行裂纹故障加工，深度分别为1、2、5、8 mm。在中间轴大齿轮上进行断齿故障加工，断齿宽度分别为2、5、10 mm。将采集到的齿轮箱振动信号按正常、裂纹深度由浅到深、断齿宽度由窄到宽依次标记为xF1,xF2,…,xF8，每个信号均包含120 000个数据点。以裂纹深度为5 mm的齿轮箱振动信号xF4为例进行分析，其步骤如下：

1) 利用带有高频谐波的LCD算法对xF4进行分解，得到10个ISC分量以及1个趋势项u(t)。

2) 对重组信号筛选。根据式(6)、(7)估算融合所需的ISC分量个数为2，并利用式(8)、(9)分别计算每个ISC分量的峭度时间序列与原始信号峭度时间序列的互相关系数，结果依次为4.27×10-3、4.21×10-2、1.89×10-2、5.87×10-2、2.15×10-2、4.78×10-3、6.03×10-3、4.99×10-2、1.31×10-1、9.58×10-2。

以互相关系数绝对值最大为筛选准则，所选取的分量为ISC9和ISC10，其频域如图1所示。可以看出：经LCD分解和ISC分量筛选后，信号分量能够有效地捕捉到故障频率132 Hz及其倍频、周边故障信息丰富的边频带，以及频率13.33 Hz等这些敏感特征信息，这就可以剔除噪声分量等干扰，抓取包含断齿故障频率的敏感特征信息。

3) 取X=10，对ISC9、ISC10两个分量分段去均值处理并进行双谱估计。齿轮正常、裂纹故障和断齿故障的双谱等高线分布图分别如图2-4所示。

由图3可以看出：1)双谱幅值的非零成分为信号中的非高斯噪声成分，这表明振动信号具有明显的非高斯特性；2)图谱聚集性随裂纹深度增加而不断增大，表现出了复杂的耦合特性。这是因为：故障发生后，齿轮内部运行状态受到影响，固有频率因发生改变而影响周围零部件的耦合程度，使得振动信号中的非高斯成分大幅增加，其双谱幅值明显增大。

由图4可以看出：1)随着断齿宽度的增大，图谱逐渐向中心聚集，故障频率位于图谱峰值处，而边缘的高频谐波逐渐减少；2)从幅值上看，振动信号中的非高斯成分随断齿宽度的增大而增多，其特征频率处的双谱幅值也随之增大。

由图2-4可以看出：与故障状态相比，正常状态下的双谱幅值明显较小。这是因为：在正常状态下，齿轮箱振动信号的高斯成分占主要部分，而高斯噪声的双谱幅值为0。

结合图3、4可知：双谱分布能在一定程度上反映故障变化过程；同类型故障的双谱分布具有一定相似性[16]，且与不同类型故障相比存在明显差异，由此可大致区分不同的故障类型。但仅在平面图上分析振动信号双谱幅值的变化难以对故障程度量化描述。因此，为更好研究故障变化规律并为剩余寿命预测奠定基础，需要在双谱分析基础上进行量化处理。

4) 通过式(13)、(14)可得到xF4的LCD-BIE特征量值为6.838。按上述方法分别计算齿轮箱振动信号的LCD-BIE及其相应的特征量值。

3.2 与其他特征提取方法的对比

为说明本文特征提取方法的有效性，分别计算xF1，xF2，…，xF8经LCD后各阶段的能谱熵(LCD-spectrum Entropy,LE)[17]，及经LCD分解但未进行分量筛选与双谱分析处理后的双谱熵BIE1，结果见表1。可以看出：随齿轮故想障程度的加剧，各特征量熵值大体呈下降趋势；LCD-BIE中敏感信息的能量较为集中，其熵值要小于LE和BIE1，说明其特征表征能力较好。

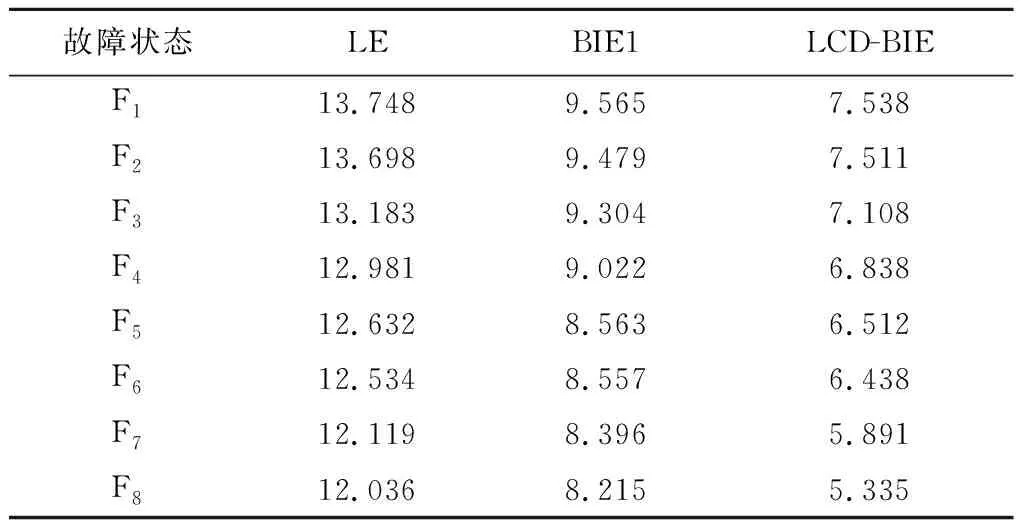
表1 不同故障状态的特征量值

对表1中各特征量进行归一化处理，绘制成曲线，如图5所示。图5描述了归一化后不同故障下各特征量的变化过程。一般认为一个好的特征曲线应是随着故障程度的加深单调递增或单调递减。

通过对比图5中的3条曲线可知：

1) LE曲线对裂纹故障由1 mm加深至2 mm过程反映较敏感，但对其他故障状态表征效果不理想。这是因为：未筛选过的ISC分量中仍存在其他分量的干扰；能谱熵不具备双谱熵消除高斯噪声的优势。

2) BIE1曲线对整个故障变化过程具有相对较好的表征能力，但由于分量融合前未做筛选处理，导致所提取故障特征包含成分复杂，整体对故障的敏感度不够高，尤其体现在特征曲线单调递减趋缓。

3) LCD-BIE曲线避免了干扰成分和消除了高斯噪声影响，其熵值最小，且能提取更完整的特征信息，对故障状态具有良好的表征能力。

3.3 故障特征值的检验

故障状态识别是评价故障特征表征能力的重要方面。为了检验本文故障特征提取方法的有效性，采用训练好的支持向量机(Support Vector Machine,SVM)定量评价所提取的特征量对不同故障的识别能力[18]。将试验中所采集的F2，F3，…，F8状态下各信号的2 400个数据点作为一组样本，各状态下各取50组样本，共350组数据样本，计算LE、BIE1、LCD-BIE特征量值。所有的特征量不同特征量对归一化到[0，1]，利用训练好的SVM进行分类识别，计算2种故障状态的识别率，结果如表2、3所示。

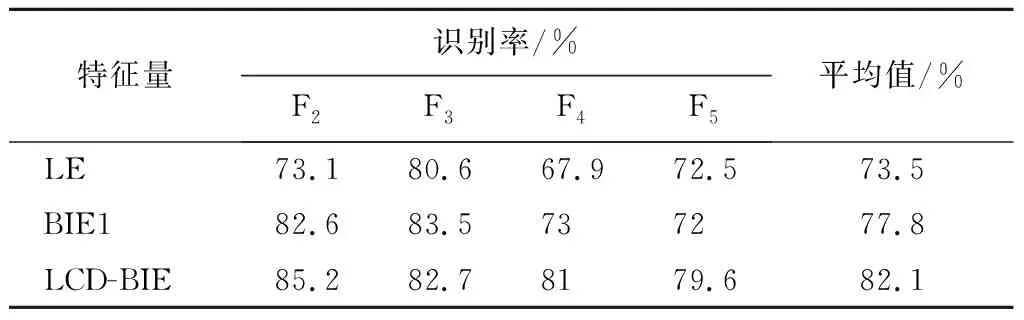
表2 不同特征量对裂纹故障的识别率

表3 不同特征量对断齿故障的识别率

由表2、3可以看出：LE识别率较低；BIE1对断齿故障的识别率高，但对裂纹故障的识别能力较差；LCD-BIE整体识别率最高，仅对个别故障状态的识别存在一定局限性。因此，LCD-BIE是有效的特征量，能够相对准确地识别设备退化状态。分析其原因为：LCD-BIE经过信号筛选可以更有效提取关键故障信息；而LE包含较多噪声成分,稳定性相对较差；BIE1比LE敏感度较高，但未筛选的信号成分依然复杂，因此稳定性差于LCD-BIE。

4 结论

笔者首先利用LCD分解去除信号高频噪声，再采用相关方法筛选出有用ISC分量，最后对融合后信号进行双谱分析，能够有效地提取出故障特征率。主要结论如下：

1) 齿轮故障信号具有非高斯特性，而噪声和其他干扰分量往往是高斯信号，利用双谱分析能够抑制振动信号中的高斯噪声，准确地提取信号中的故障特征信息。

2) 采用BIC准则和峭度时间序列互相关系数相结合的方法对ISC分量进行选取，能够有效地去除干扰分量，抓取有用信息，提高特征的敏感度，从而进一步改善对故障状态的表征能力。

3) LCD-BIE故障特征提取方法能有效提取正常状态下的齿轮故障特征，提高了对故障的识别能力。但在变工况条件下，振动信号将更加复杂，故障信号与噪声之间的关系有待于研究，算法的适用性还要进一步验证。