倾斜螺纹孔射流传热特性的数值研究
徐亮,熊堰宏,席雷,高建民,李云龙
(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.广东西安交通大学研究院,528000,广东佛山)
冲击射流作为一种最有效的单相介质对流传热强化技术,被广泛应用于燃气轮机涡轮叶片冷却,电子元器件冷却,纺织品、纸张干燥,冶金工业等。在实际应用的某些场合,由于空间受限,射流孔不得不采用倾斜布置,如涡轮叶片前缘冲击冷却孔的布置形式。近年来,诸多学者发现在提升靶面传热性能方面,旋转冲击射流比传统的圆孔射流要好得多[1-4]。虽然在涡轮叶片中使用旋转冲击射流进行冷却会使叶片结构变得更加复杂而难以加工,但随着金属增材制造技术的发展,为设计和制造复杂冷却结构的涡轮叶片提供了可能[5-6]。根据现有文献,倾斜态冲击射流传热研究采用的射流喷嘴基本以圆孔和狭缝为主[7-17],而对旋流喷嘴下的冲击射流传热特性鲜有研究,因此有必要研究倾斜态旋转冲击射流的传热特性,为设计高效新型的冲击冷却方法提供重要参考。
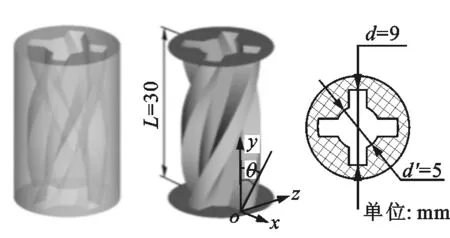
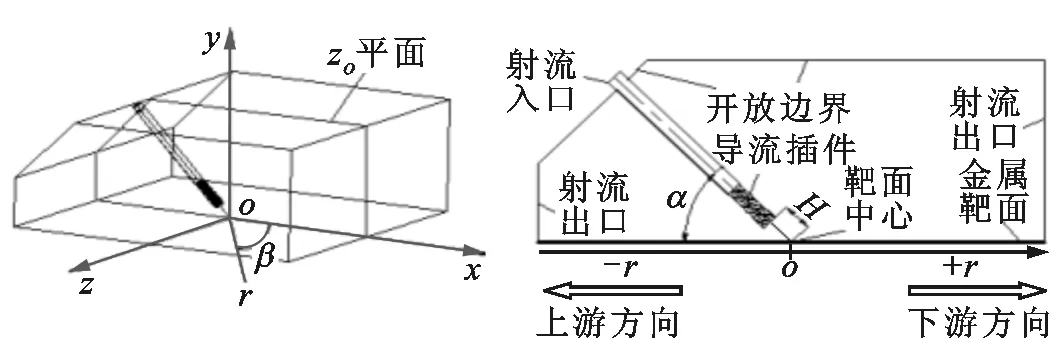
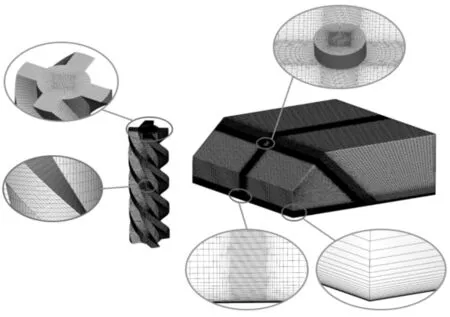
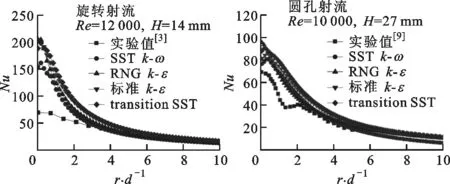
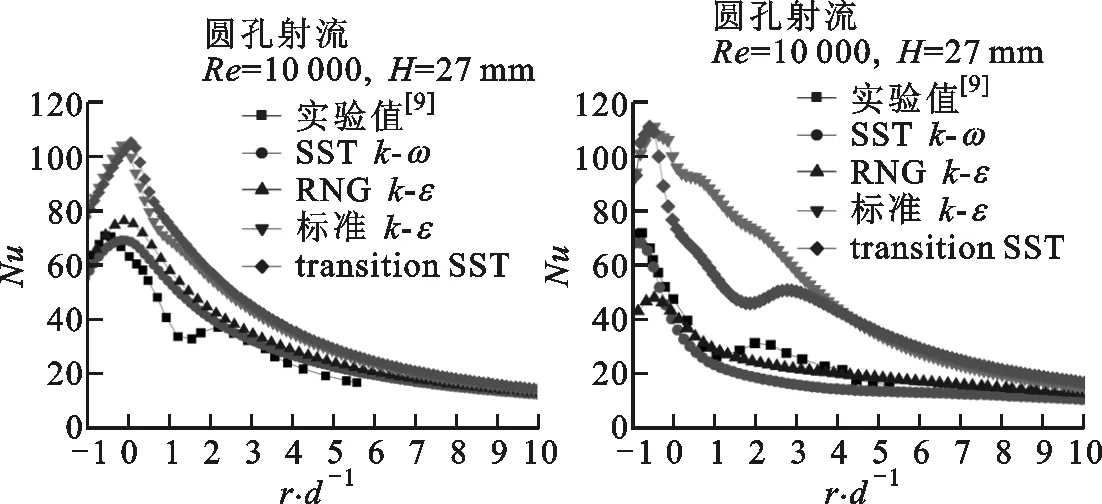
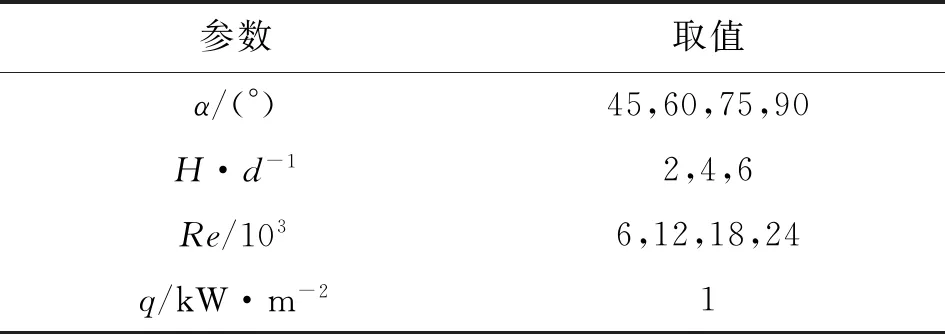
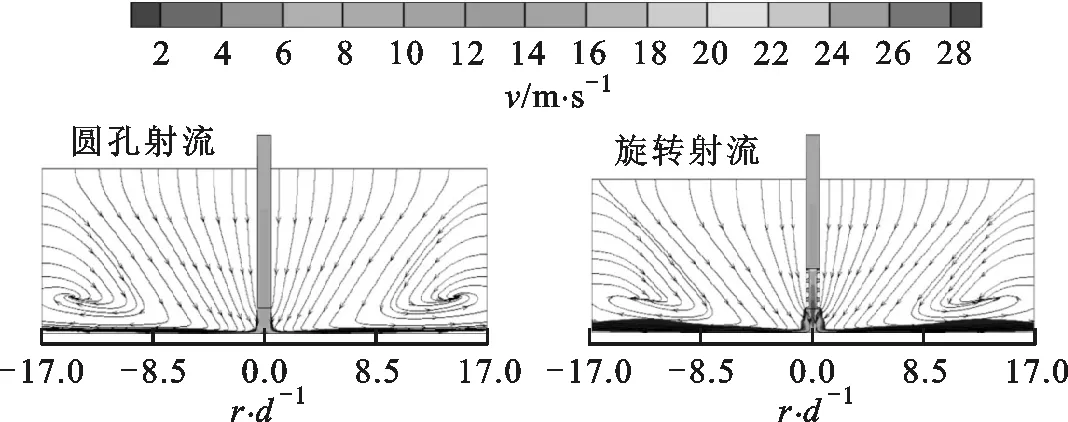
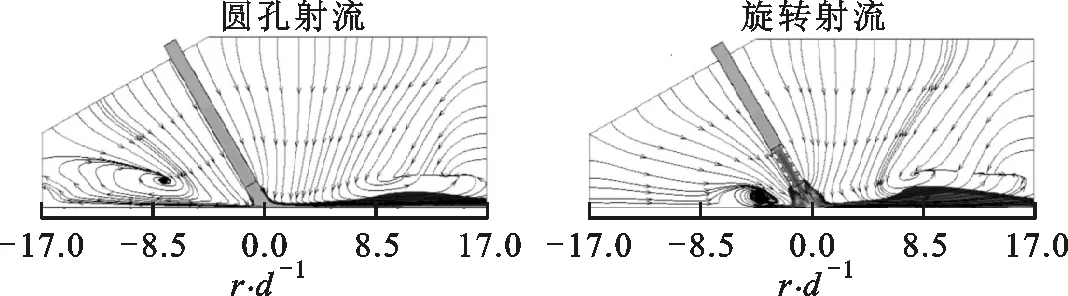
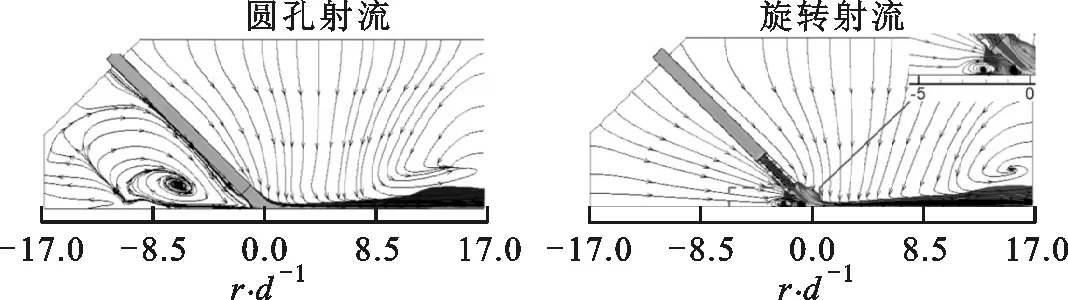
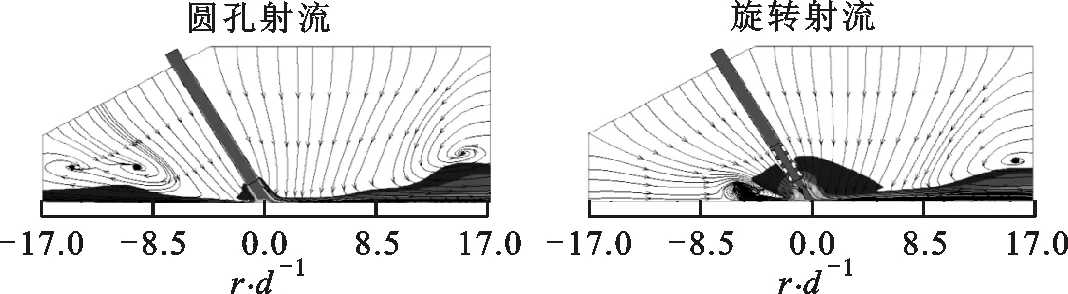
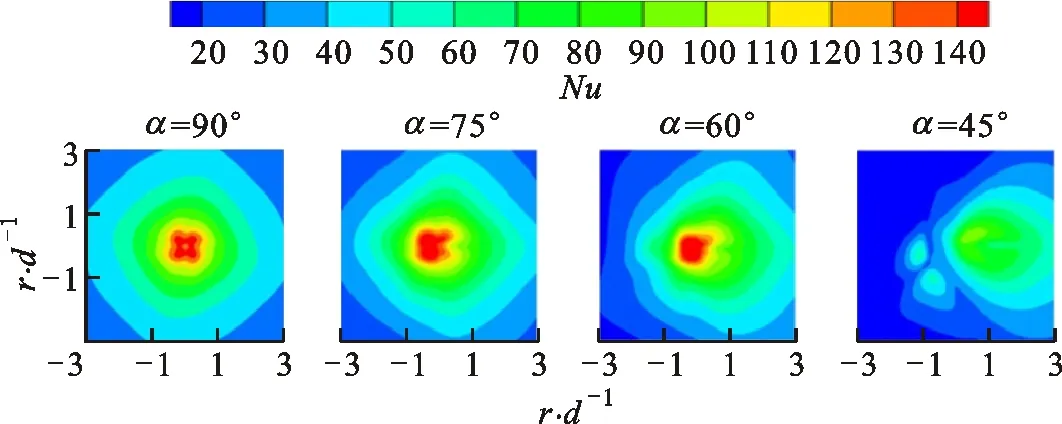
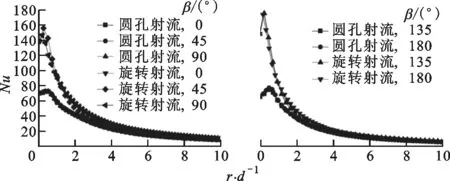
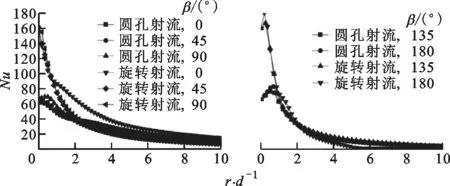
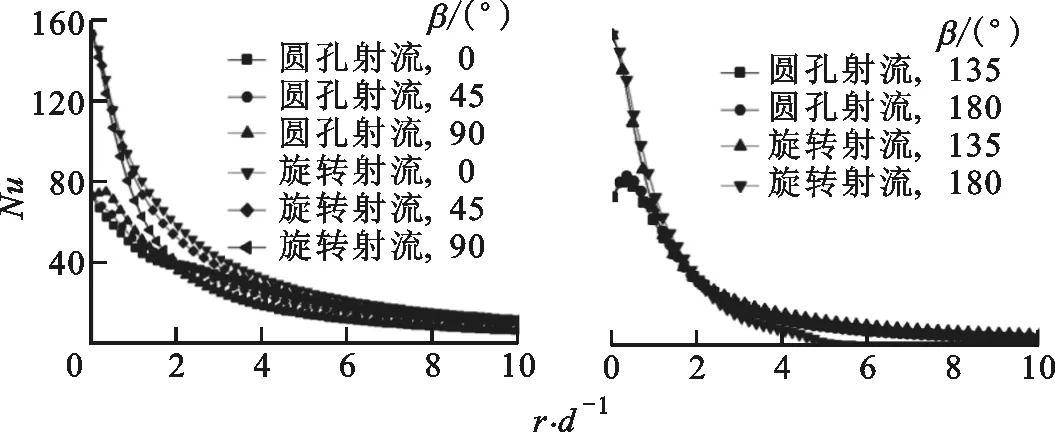
在实验研究方面,Yoon等研究了倾斜狭缝冲击射流对加热板传热特性的影响,指出随着倾斜角减小,滞止点向板面上方移动,板面上方局部的努塞尔数Nu大于板面下方的Nu[7]。Yan等研究了倾斜圆孔冲击射流,发现冲击角和冲击距离越小,最大传热点向上游方向转移越明显[8]。Donovan等的实验发现,倾斜态圆孔射流的Nu峰值点与滞止点重合,滞止点位移与射流冲击角的大小成反比,而与射流冲击距离无关[9]。Sparrow等认为圆孔射流随着倾斜角的增大,冲击靶面Nu峰值点远离射流冲击中心,最大传热点上游局部传热系数下降较下游要快,且最大传热系数下降约15%~20%[10]。Goldstein等对倾斜圆孔射流时板面的局部温度和热流密度进行了测量,得出在冲击距离和冲击角一定的情况下,垂直射流近峰区域(0 在数值模拟方面,Bhagwat等采用V2F模型研究了倾斜态圆孔冲击射流,在板面倾斜的情况下,其上端Nu也急剧减小,而在板的下部,Nu减小较为缓慢[15]。Chuang等采用k-ε模型分析倾斜冲击射流,结果表明,当倾斜角减小时,左侧再循环区域减小,右侧再循环区域增大,靶面上的最大压力区域位置向左移动并且数值减小[16]。陈庆光等的数值模拟结果表明,倾斜角减小时,左侧回流区变小,而右侧回流区变大,最大压力区和最大湍动能区向流场的左侧移动[17]。 综上可知,倾斜入射的冲击射流能导致靶面Nu峰值点向靶面上游方向转移,且最大Nu随着倾斜角的减小而增大,但会导致靶面的传热性能明显恶化。在文献[3]中,本课题组对类螺纹孔旋转垂直射流进行了研究,发现螺旋角为45°的类螺纹孔旋转冲击射流使得靶面有较好的对流换热效果,本研究对该螺纹孔在倾斜态时射流冲击靶面的流动和传热特性做了进一步的探索。首先基于文献[3]中垂直旋转冲击射流和文献[9]中倾斜圆孔冲击射流的实验数据,选择适合计算倾斜态旋转冲击射流流动及传热特性的湍流模型,论证了本文发展的倾斜态旋转冲击射流的数值计算方法的可靠性。然后,通过改变倾斜角α、冲击距离H/d、入口雷诺数等影响因素,并结合圆孔冲击射流,较为详细地对比分析了倾斜态45°类螺纹孔射流和旋转射流冲击靶面的流动和换热特性。 本文选取文献[3]中的螺旋角为45°的类螺纹孔来形成旋转射流,其基本尺寸与文献[3]中保持一致,类螺纹结构和倾斜旋转射流计算模型如图1所示。在倾斜态,由于旋转冲击射流靶面温度分布不均匀,为了数据的一致性,本文选取靶面上直线r(直线r与x轴正向夹角(方位角)为β)和平面z0(xoy平面)的数据进行分析,其位置如图1b所示。靶面上0°≤β≤90°的范围为靶面下游方向,90°<β≤180°的范围为靶面上游方向。 (a)类螺纹孔结构 (b)计算模型图1 类螺纹孔结构及倾斜旋转射流计算模型 (a)多块结构化网格 (b)网格独立性检验(α=45°,H/d=4)图2 结构化网格及网格独立性检验 在计算模型中,入口管道长为10d,以确保气流在管道内已充分发展,三维模型长×宽×高为300 mm×300 mm×110 mm。计算网格为多块结构化网格,采用ICEM CFD软件绘制,近壁面第一层网格尺寸为0.001 mm,网格增大因子为1.2,网格模型如图2a所示。为了消除网格对计算结果的影响,进行了网格独立性检验,以靶面Nu变化在2%以内视为计算网格具有网格无关性,如图2b所示。计算求解采用商业软件Fluent18.0,湍流模型选用SSTk-ω模型,求解方法为压力基Simple算法,选取二阶迎风格式。模型边界条件如下:射流入口为质量流量入口,入口气流温度为300 K,湍流度为5%;不锈钢靶面厚度为1 mm,靶面热流密度q=1 kW/m2。 本文的数据处理方法如下。 局部传热系数为 c=q/(Tw-Tin) (1) 雷诺数为 (2) 努塞尔数为 Nu=cd/k (3) 平均努塞尔数为 (4) (a)α=90°(q=1 kW/m2) (b)α=90°(q=15 kW/m2) (c)α=75°(q=15 kW/m2) (d)α=60°(q=15 kW/m2)图3 不同湍流模型的靶面Nu(β=0°) 为验证本文计算模型的可靠性,选取文献[3]中旋转射流实验数据和文献[9]中不同倾斜角(60°、75°、90°)的圆孔射流实验数据进行验证,图3给出了不同湍流模型计算出的靶面Nu。从图3a中可以看出,由于垂直旋流时滞止区域(r/d≤3)是层流和过渡发展区域,故采用湍流模型的计算结果都明显偏高,误差较大(可达30%以上)。对于圆孔冲击射流,湍流模型计算结果都很难捕捉到靶面上第二峰值的波动,这与文献[15]数值计算结果一致。就与实验结果的吻合度来说,使用SSTk-ω模型的计算结果与上述文献的实验数据最为接近,所以本文采用该模型来计算倾斜条件下的旋转冲击射流。 为研究倾斜角为45°的类螺纹孔冲击射流的流动特性和传热特性,本文主要从射流倾斜角、冲击距离、雷诺数这些因素来探讨它们对射流空间流场以及靶面传热特性的影响,并结合传统圆孔进行对比分析,具体选择的工况参数如表1所示。 表1 本文研究的工况参数 图4为Re=6 000、H/d=2时不同倾斜角下圆孔射流和旋转射流在z0平面内的流线及速度分布图。当垂直射流(α=90°)时,无论是圆孔射流还是旋转射流,流场和速度场均呈对称分布。在图4a中可以明显看到光滑圆孔高速冲击射流对周围空气的卷吸作用,使得射流与外部卷吸而入的气流在r/d=±13.5处形成旋涡。在垂直旋转射流空间中,由于旋转射流对外部气流的卷吸作用更强,可以看到旋涡的位置相对于光滑圆孔射流更加靠近靶面中心,出现在r/d=±12处。同时,由于类螺纹内螺纹的阻塞作用,更多的气流涌现在孔中心线区域射出,相比光滑圆孔垂直射流中心线射流速度要更大,其势流发展作用区更长。 (a)α=90° (b)α=75° (c)α=60° (d)α=45°图4 不同倾斜角下圆孔和旋转射流在z0平面内的流线及速度分布图 当α=75°时,圆孔射流有较多的气流向板面下游方向流走,射流对板面上游方向气流卷吸作用增强,使得上游方向壁面射流发生位置相对于垂直射流有所提前,因而形成的卷吸旋涡在向靶面中心靠近的同时还有所扩大。对于旋转射流,靶面上游的旋涡同样在向靶面中心移动,与圆孔射流所不同的是此时的旋涡有所减小并且出现了两个牵连旋涡。这是由于向靶面上游方向流动的气流与靶面上游的卷吸而入的气流相互冲突,先在r/d=-7处形成一个旋涡,此外旋转射流存在一个切向速度,因而与后面卷吸而入的气流在r/d=-15处再次形成一个旋涡;对于旋转射流的下游区,由于旋流壁面射流的提前,可以看到出口区域的夹带旋涡位置也随之提前,同时壁面边界层的厚度也相应增大,这将会削弱壁面这一区域的换热性能。 当倾斜角进一步减小到60°时,圆孔射流靶面上游方向的旋涡移动到r/d=-7处,此时的旋涡进一步扩大,但仍有部分气流从上游方向逸出;在靶面下游方向,此时的壁面射流发生位置更加提前,壁面射流速度衰减较快,在远离靶面中心的低速区域边界层逐渐扩大,使得下游方向的旋涡几乎无法完全形成,如图4c所示。旋转射流对外界气流强烈的卷吸作用使得在靶面上游方向几乎没有射流逸出,但由于反弹的气流含有旋转切向速度分量,将在射流滞止区域附近r/d=-4处形成一个很小的类壁角旋涡;在靶面下游方向,同样由于滞止区后部的旋流壁面射流的提前,先与卷吸进入的气流形成一个碰撞旋涡,随后由于出口气流速度很大,在其上部又形成了一个夹带旋涡,因而在图4c中可以看到下游出口区域有两个旋涡。 当倾斜角增大到45°时,圆孔形成的射流几乎全部沿着下游方向流走,靶面上游方向气流速度极低,旋涡扩展到最大,上游方向基本无气流逸出,因而该区域的壁面对流换热效果削弱最强。对于旋转射流:卷吸而入的外部气流流速大于向上游部分流动的射流流速,再由于导流元件距离靶面很近,气流发展空间十分狭小,因而仅在螺旋导流元件的滞止区内产生两个较小的滞止旋涡;在下游方向,由于壁面射流的位置提前,使得此时的旋涡相对于α=60°时略微向外扩展。 总体而言,对于光滑圆孔射流,减小倾斜角会使靶面上游方向的旋涡向靶面中心移动,旋涡会逐渐扩大,而下游方向的旋涡无明显变化。对于旋转射流,随着倾斜角的减小,靶面上游方向的旋涡在向靶面中心移动的同时逐渐缩小,而下游方向旋涡的数量、大小及位置随着倾斜角的改变有相应变化。在同一倾斜角下,靶面上游方向旋涡的位置更加靠近靶面中心,而且旋转射流轴向速度夹带能力很强,所形成的旋涡要比圆孔射流所形成的旋涡小,且位置更向出口区域(r/d=-17)发展。其次,对比旋转射流和圆孔射流的速度云图,可以明显发现,由于导流元件的影响,旋转射流出口处气流流速明显比圆孔射流要高,这将使得旋转射流靶面中心滞止区附近的对流换热强度高于圆孔射流。 图5为Re=6 000、α=60°的圆孔和旋转射流在z0平面内的流线及速度分布图。相对于H/d=2(图4c)的情况,H/d=4时的圆孔射流,靶面上游方向卷吸气流形成的旋涡缩小,位置出现在r/d=-9处,旋涡远离靶面中心,而在靶面下游方向的旋涡同样远离靶面中心。对于旋转射流,由于在上游区域的空间增大,从旋流喷嘴流出的气流反弹后能得以充分发展,这样在滞止区附近的上游方向旋涡明显增强,而在下游区域由于轴向气流的流出和卷吸进入的气流在出口区域仅形成了一个旋涡。H/d=6时,圆孔射流上游和下游方向的两个旋涡都更加远离靶面滞止中心,然而旋转射流上游方向旋涡在远离靶面滞止中心发展的同时还出现了第二个卷吸旋涡,对于下游区域,主要是轴向速度的气流在大空间内较为顺畅地流出,夹带气流与卷吸而入的气流碰撞在出口区域形成旋涡,因此与H/d=4时相比,靶面下游方向的旋涡没有明显的变化。 (a)H/d=4 (b)H/d=6图5 不同冲击距离下圆孔和旋转射流在z0平面内的流线及速度分布图 由图4c、图5速度分布云图可知,随着冲击距离的增大,圆孔射流和旋转射流在下游方向的速度边界逐渐加厚。与圆孔射流所不同的是,旋转射流对气流的卷吸作用更明显,因而其导流元件出口处高速气流区域扩展分布更加广泛(冲击距离越大,现象越明显)。 (a)Re=12 000 (b)Re=18 000 (c)Re=24 000图6 不同雷诺数下圆孔和旋转射流在z0平面内的流线及速度分布图 图6为α=60°、H/d=2时不同雷诺数下圆孔和旋转射流在z0平面内的流线及速度分布图。结合图4c可以看出,当雷诺数由6 000增大到12 000时,靶面上、下游方向旋涡均会随之远离靶面滞止中心。当Re=18 000时,圆孔射流上游方向出现第二旋涡(r/d=-14处),该第二旋涡是由于第一旋涡(r/d=-9处)所形成的卷吸气流和向外逸出的射流与外部吸入的气流相互碰撞而产生的。当Re=24 000时,靶面上游方向只有一个旋涡,下游方向旋涡与Re=18 000的流动特征相比无明显变化。对于旋转射流来说,增大雷诺数,靶面上游旋涡无明显变化,而下游方向出口区域的旋涡的位置随着雷诺数的改变会产生相应的变化,但大小变化不明显。 从图6中速度云图来看,无论是对于圆孔射流还是旋转射流,增大雷诺数,靶面喷出的气流速度也自然会随之增大。在雷诺数和倾斜角相同的情况下,圆孔射流上游方向速度较旋转射流要大(Re=24 000时最为明显),而旋转射流由于导流元件的旋流作用,使得喷嘴出口附近气流高速区域较圆孔射流的区域范围要大得多。 图7为Re=6 000、H/d=2时不同倾斜角下圆孔射流和旋转射流冲击靶面的Nu云图。从图7中可以看出,减小倾斜角使得圆孔射流和旋转射流靶面Nu分布均匀性逐渐降低,不再呈对称分布,这势必会造成靶面上产生更不均匀的温度分布。在同一倾斜角和Re下,对比分析圆孔射流和旋转射流Nu云图可以明显发现,旋转射流的靶面Nu分布更为不均匀,尤其是当倾斜角为45°时,旋转射流的靶面Nu均匀性最差。从Nu的大小来看,旋转射流靶面中心附近Nu明显高于圆孔射流,这是因为同一射流流量下旋转射流孔出口的中心区域具有更大的出口速度。 (a)圆孔射流 (b)45°类螺纹孔旋转射流图7 不同倾斜角下圆孔和旋转射流靶面的Nu云图 图8为H/d=2、Re=6 000时不同倾斜角下的圆孔射流和旋转射流靶面Nu随径向位置的变化曲线。从图中可以看出,当垂直冲击射流(α=90°)时,无论是圆孔射流还是旋转射流,靶面Nu呈对称分布,且均出现小冲击距离下的弱双峰值分布。但是,在射流冲击核心区(r/d≤1)圆孔射流和旋转射流的靶面Nu存在很大差异。旋转射流靶面中心Nu及其峰值相对于圆孔射流分别增长了98.5%、114.6%。就Nu峰值的径向位置而言,因为螺旋孔中心的高速区域相对较窄,表现出的Nu峰值位置比圆孔要更接近滞止中心点。 (a)α=90° (b)α=75° (c)α=60° (d)α=45°图8 不同方位角下射流靶面局部Nu随径向位置的变化曲线 当α=75°时,可以明显观察到,无论是哪一种冲击射流,靶面Nu峰值点均在靶面上游方向。此时,旋转射流靶面中心和最大Nu相对于圆孔射流分别增长了125.9%、126.4%。当倾斜角从90°减小到75°时,对于圆孔射流,靶面Nu分布无明显变化,而对于旋转射流,靶面Nu虽无明显变化,但最大Nu增大了14.4%。 当α=60°时,无论是圆孔射流还是旋转射流,靶面Nu峰值点仍处于上游方向,此时旋转射流靶面中心Nu及其峰值相对于圆孔射流分别增大了139.9%、116.3%。也可以看到,从垂直射流倾斜到60°时,螺纹孔和圆孔射流靶面Nu峰值的径向位置并没有因射流倾斜而出现很明显的变化,同时就Nu的大小,倾斜也并没有减弱两种喷嘴下射流滞止区附近的换热能力。 当α=45°时,旋转射流最大Nu出现在下游方向,而圆孔射流最大Nu仍处于上游方向,此时旋转射流靶面中心和最大Nu相对于圆孔射流分别增大了15.48%、24.25%。在靶面下游方向,旋转射流靶面不同方位角的Nu分布差异比圆孔射流大,而在上游方向,两种射流不同方位角的Nu分布差异相对较小。相对于α=60°的情况,α=45°时的圆孔射流靶面中心和最大Nu无明显变化,但旋转射流靶面中心和最大Nu分别下降了53.3%、46.8%。由此可见,当倾斜角为45°时,圆孔射流对靶面传热效果影响不甚明显,但旋转射流时靶面传热能力明显恶化。 倾斜射流情况下,在射流核心区内,旋转冲击射流的冷却效果显著强于圆孔冲击射流,即使是在倾斜角为45°的情况下,旋转射流靶面中心和最大Nu仍然高于圆孔射流。造成这种现象的主要原因是旋转射流中心气流在进入射流空间具有较高的喷射速度,从而使滞止点附近区域的对流传热能力较强。当倾斜角为90°、75°、60°时,与圆孔射流相比,旋转射流对靶面的传热强化作用主要集中在r/d≤3的范围内,在气流进入壁面射流流动区域以后,旋转射流与圆孔射流的传热效果基本相当,都比较弱,Nu的值在20左右。 图9为Re=6 000、α=60°时不同冲击距离下圆孔射流与旋转射流靶面Nu分布图。当H/d=4时,圆孔射流靶面Nu峰值点在靶面上游方向,而旋转射流靶面Nu峰值点与靶面中心重合,此时旋转射流靶面Nu峰值比圆孔射流的高81.8%。H/d=4时圆孔射流靶面中心Nu与H/d=2(图8c)时相比增大了11.4%,而最大Nu基本保持不变。对于旋转射流,冲击距离从2增加到4时,靶面中心和最大Nu分别下降了3.75%、14.4%。同时也可以看出,随着冲击距离的加大,旋转射流时因切向气流在射流空间扩散范围更大,靶面高Nu从滞止点沿径向衰减要比小冲击距离下更为缓慢。 (a)H/d=4 (b)H/d=6图9 不同冲击距离下靶面Nu分布 当H/d=6时,圆孔射流和旋转射流Nu峰值点与靶面中心重合,此时旋转射流最大Nu比圆孔射流的高27.3%。H/d=6时圆孔射流靶面中心Nu与H/d=4时相比增大了15.2%,最大Nu依然保持不变。对于旋转射流,H/d=6时靶面中心Nu相对于H/d=4时下降了29.2%。冲击距离从2增加到6时,旋转射流靶面中心Nu比圆孔射流靶面中心Nu分别高139.9%、107.2%、27.3%。 图10a给出了冲击距离H/d=2、α=60°时不同雷诺数下圆孔射流与旋转射流在靶面沿x轴方向上Nu的分布情况。从图中可以看出,增大雷诺数,无论是圆孔射流还是旋转射流,均能明显增加靶面的Nu,但在较低雷诺数(Re=6 000)时,靶面Nu分布较为均匀。当雷诺数从6 000增加到24 000时,旋转射流靶面中心Nu相对于圆孔射流靶面中心Nu分别增加了118.9%、138.2%、150.5%、161.5%。图10b为H/d=2、α=60°时旋转射流和圆孔射流靶面Nu峰值分布。随着雷诺数的增加,旋转射流靶面Nu峰值与圆孔射流的差值逐渐扩大并趋于一定值,这说明增大雷诺数使得旋转冲击射流靶面换热效果提升在Re≤18 000时非常有效,但继续增大Re换热效果提升有限。 (a)靶面Nu分布 (b)Nu峰值分布图10 不同雷诺数下靶面Nu及其峰值分布 图11为Re=6 000、H/d=2时圆孔射流和旋转射流在不同倾斜角下靶面Nuave分布图。对于圆孔射流,倾斜角为45°时在靶面不同径向距离的Nuave比其他倾斜角下的Nuave降低4.9%~23.56%,而倾斜角为60°、75°、90°时,靶面的Nuave分布极为接近,这说明对于圆孔射流,改变射流倾斜角对靶面传热整体性方面影响不大。在图11旋转射流靶面Nuave图中,当倾斜角为60°、75°、90°时,靶面Nuave变化不大,但当倾斜角为45°时,靶面不同径向距离的Nuave远低于其他射流冲击角下的Nuave,下降幅度在33%~52.8%之间。与圆孔射流靶面Nuave相比,当α=90°时,旋转射流的靶面Nuave比圆孔射流的高38.5%~95.6%,α=75°时高38.7%~109%,α=60°时高34%~106%,即使在α=45°时,旋转射流靶面Nuave仍然高3.9%~10.6%。综上可知,从靶面Nuave分布来看,圆孔射流靶面Nuave分布虽然比旋转射流更为均匀,但旋转射流靶面Nuave要显著高于圆孔射流,并且当倾斜角减小为45°时,两种喷嘴射流下靶面传热效果都会出现较大程度的恶化。 (a)圆孔射流 (b)旋转射流图11 不同倾斜角下靶面Nuave分布 图12为Re=6 000、α=60°时不同冲击距离下圆孔射流和旋转射流的靶面Nuave分布图。对于圆孔射流靶面的Nuave而言,增大冲击距离,会使射流冲击核心区(r/d≤1)的Nuave降低,当r/d>1时,冲击距离的变化对靶面Nuave不构成影响。对于旋转射流,随着冲击距离的增大,靶面Nuave逐渐降低,H/d=4时Nuave比H/d=2时降低了4.5%~8.2%,H/d=6时的Nuave比H/d=4时降低了2.6%~21%。冲击距离一定时,旋转射流的靶面Nuave明显高于圆孔射流。综合分析旋转射流在Re=6 000、α=60°时不同冲击距离和不同方位角下的靶面Nuave分布情况,可以认为旋转射流在H/d≤4的情况下,靶面传热效果较好。 (a)圆孔射流 (b)旋转射流图12 不同冲击距离下靶面Nuave分布 图13为圆孔射流和旋转射流在α=60°、H/d=2时不同雷诺数下的靶面Nuave分布图。随着雷诺数的增大,靶面Nuave也随之增大,旋转射流Nuave的增加幅度高于圆孔射流。对于圆孔射流来说,在不同雷诺数下,靶面Nuave径向衰减速度变化不大,而对于旋转射流,随着雷诺数的增大,靶面Nuave的径向衰减速度也逐渐增大。在同一雷诺数下,旋转射流的靶面Nuave要高于圆孔射流,但从靶面传热均匀性方面考虑,圆孔射流的靶面Nuave分布更为均匀。 (a)圆孔射流 (b)旋转射流图13 不同雷诺数下靶面Nuave分布 本文研究了射流倾斜角、冲击距离、射流雷诺数对旋转冲击射流的流场以及靶面Nu的影响,并与圆孔射流进行了对比,主要结论如下。 (1)通过与实验数据的对比,验证了SSTk-ω模型能较好地模拟倾斜情况下的旋转冲击射流。改变射流冲击倾斜角、冲击距离对圆孔射流和旋转射流的流场和速度场会产生较大影响,而改变射流雷诺数对旋转射流的流场结构改变不甚明显。 (2)在雷诺数和冲击距离一定的条件下,当减小射流冲击倾斜角时,圆孔射流靶面Nu及其峰值以及靶面Nuave变化不甚明显。对于旋转射流,减小倾斜角会使靶面中心Nu及其峰值先增大后减小;在同一倾斜角下,旋转射流靶面中心Nu及其峰值明显高于圆孔射流。当α=90°,75°,60°时,旋转射流靶面Nuave变化不大,而α减小到45°时,靶面Nuave明显减小。 (3)在雷诺数和冲击角一定的情况下,当增大冲击射流距离时,圆孔射流冲击核心区(r/d≤1)靶面Nu会有所升高,而靶面Nuave变化不大。对于旋转射流,靶面射流冲击核心区(r/d≤1)的Nu会随着冲击距离的增大而减小,但旋转射流冲击核心区Nu始终高于圆孔射流。此外,冲击距离一定时,旋转射流靶面Nuave要明显高于圆孔射流。 (4)在倾斜条件下,当冲击距离较小时增大雷诺数,两种喷嘴射流的靶面Nu均增大,旋转射流靶面的传热性能提升更加明显,然而在Re≥18 000时继续增大雷诺数,换热效果提升有限。1 模型及数值计算方法

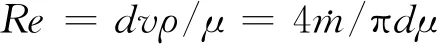
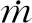
2 数值计算结果及分析
2.1 流场特性





2.2 靶面的局部传热特性



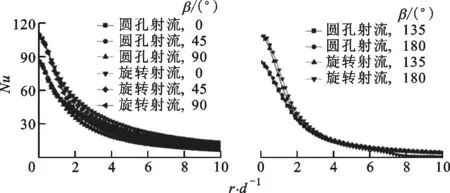
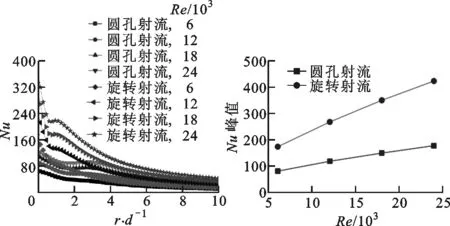
2.3 靶面平均努塞尔数
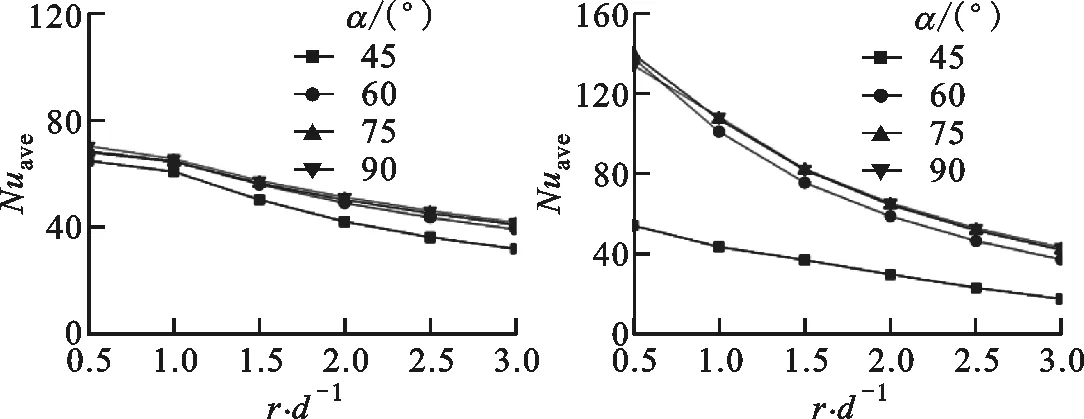

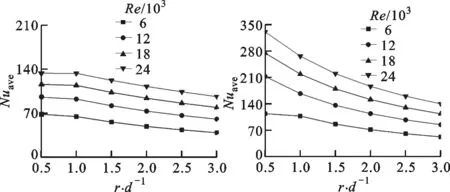
3 结 论

