燃煤电站锅炉炉膛结渣特性计算分析

刘丹,周熙宏,杨冬,刘朝晖,裘立春,滕敏华

(1.西安交通大学动力工程多相流国家重点实验室,710049,西安;2.浙江浙能技术研究院有限公司,311121,杭州)

当前,我国电力行业仍然以煤为主要消费能源,加之电站锅炉燃用煤种的含硫量、含灰量均较高,使得受热面极易造成积灰和结渣。在经过了几十余年的升级和创新之后,新型电站锅炉以其较高的燃煤利用率和优良的环保性能已逐步在国际上推广投运,并且成为我国大力建设的主要机组,但是炉膛结渣这一问题仍然严重影响着锅炉的安全运行。

由于灰的热阻较锅炉受热面钢材的大,使得水冷壁传热恶化,进而导致炉膛出口烟温升高,这又使得过热蒸汽温度偏高,不仅危害过热器,还会导致汽轮机发生事故。同时,传热阻力增大需通过增加给煤量来维持锅炉满负荷运行,使得炉膛出口烟温进一步升高,这一恶性循环使得电站锅炉常发生一系列事故。大块的渣掉落也会砸坏水冷壁和灰斗,使灰斗发生堵塞甚至炉膛熄火。此外,积灰和结渣带来的高温腐蚀、磨损也给锅炉安全运行造成了一定的危害。因此,对锅炉炉膛结渣程度及发展趋势进行有效监测就显得尤为重要。

国内外学者对电站锅炉炉膛结渣监测进行了大量的研究,炉膛结渣情况监测方法包括测量法和预测法[1-6]。其中,测量法有利用红外照相设备直接观察炉内结渣程度、利用热流计或者热电偶通过测量结渣带来的热流变化或炉膛出口烟温变化从而监测结渣程度等。Valero等利用红外成像相机直接测量水冷壁辐射发射率,从而判断水冷壁结渣情况[7],不过由于红外成像相机安装困难,且难以长时间在炉膛高温环境下工作,该方法仅停留在实验室阶段。高继录等开发出一种微型超高温热流计,用于测量水冷壁热流密度从而实现炉膛结渣情况的实时监测[8],但该超高温热流计造价昂贵、维护困难,一定程度上限制了该技术的推广及应用。徐立刚等建立了炉膛辐射传热模型,并基于烟温软测量方法计算炉膛污染率[9],但该模型仅适用于负荷较为稳定的工况,负荷变化较快工况下监测结果波动较大。预测法包括基于燃煤特性的单一指标和多指标综合评判方法、人工神经网络方法、模糊数学方法以及模式识别方法等。杨冬等利用反平衡法求得炉膛出口烟温,并根据炉膛平均热有效性系数得到清洁因子,根据清洁因子大小判断炉膛结渣情况[10]。任林等先基于模糊C均值聚类法对数据进行预处理,然后利用粒子群优化的支持向量机建立了电站燃煤结渣预测模型[11]。邓喆利用经典3层BP神经网络,对炉膛整体结渣情况进行了预测[12]。预测法虽然较测量法存在一定的误差,但实现起来更为容易,因此在各大电厂得到了推广使用,而现有文献在炉膛局部结渣情况方面的报道较少。

本文分别以一台300 MW级亚临界、一台600 MW级亚临界以及两台1 000 MW级超超临界锅炉机组为研究对象,根据锅炉机组参数、燃煤数据,利用单一指标与多指标燃煤特性判别方法、模糊神经网络方法对该电站锅炉炉膛结渣情况进行了预测。针对300 MW级亚临界锅炉机组建立了膜式水冷壁实际热流密度的计算模型,并根据现场实测结果,利用基于污染系数的神经网络对该电站锅炉炉膛局部结渣情况进行了实时预测。最后,对单一指标与多指标的燃煤特性判别方法、模糊神经网络方法以及基于污染系数的神经网络方法进行了比较与分析。

1 基于燃煤特性的炉膛结渣模型与预测

锅炉炉膛结渣情况与燃煤特性有着密切的关系,目前国内常用的基于燃煤特性的炉膛结渣模型主要包括单一指标、多指标综合预测模型。

1.1 单一指标预测模型

单一指标预测模型根据灰分特性对炉膛结渣倾向进行预测,如软化温度t2、硅铝比RSiAl、碱酸比RBA、硅比RG、硫分结渣指数RS等,其中RBA、RG以及RS的计算式如下

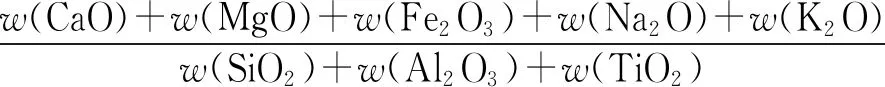
(1)

RG=100w(SiO2)/[w(SiO2)+w(CaO)+w(MgO)+w(Fe2O3)+1.11w(FeO)+1.43w(Fe)]

(2)

(3)

式中:w为质量分数;St,ar为煤的收到基硫分;Mar为煤的收到基水分。表1给出了单一指标预测模型评判炉膛结渣情况的标准,其中L、M、S分别代表轻微、中等、严重3种结渣程度。

表1 单一指标预测模型评判标准

1.2 多指标综合预测模型

(1)综合指数R预测模型。该模型根据我国动力用煤煤灰特性资料,通过对各指标(t2、RBA、RG、RSiAl)评价再加权得到:R<1.5为轻微结渣,R=1.5～2.5为中等结渣,R>2.5为严重结渣。R的计算式如下

R=5.414 5-0.002 3(t2/℃)+1.237 2RBA-0.018 9RG+0.282RSiAl

(4)

(2)RTSQ预测模型。该模型利用模糊数学方法根据熔点结渣指标RT、变形温度t1、软化温度t2、硫分结渣指数RS、硅比RG以及黏度结渣指数Rv与锅炉容积热负荷qv和断面热负荷qF之间的关系对炉膛结渣情况进行综合评价。根据所建立的各指标与qv、qF间的拟合公式得出各结渣指标所对应的高限热负荷qvi(G)、qFi(G)及低限热负荷qvi(D)、qFi(D),将多个高限热负荷和低限热负荷分别取其中间值得到各自高限热负荷qv(G)、qF(G)和低限热负荷qv(D)、qF(D)的估计值。表2给出了根据炉膛容积热负荷和断面热负荷进行预测的标准。

表2 RTSQ综合预测模型评判标准

1.3 实例计算及分析

某300 MW燃煤发电机组锅炉为亚临界参数变压运行、自然循环、四角切圆燃烧、一次再热、单炉膛平衡通风、固态排渣、全钢构架的Π型汽包炉,过热、再热蒸汽温度分别采用3级喷水和摆动燃烧器调温方式,生产厂家是东方锅炉(集团)股份有限公司。炉膛宽×深×高为13.35 m×12.829 m×54.3 m。锅炉燃用煤种为神府东胜煤,该煤种的煤质及灰分成分分析如表3所示。

表4为根据单一指标和多指标综合预测模型对该锅炉炉膛结渣情况进行预测的结果,qv(D)=178 255.85 kJ/(m3·h),qv(G)=213 947.26 kJ/(m3·h),qF(D)=4 668 762.81 kJ/(m2·h),qF(G)=49 316 465.51 kJ/(m2·h)。

由表4可知:单一指标和综合指标的8项预测结果中有5项显示严重结渣,2项显示中等结渣,1项显示轻微结渣,据此可判断该锅炉机组燃用该煤种时,炉膛结渣情况为严重结渣。同时,该结果也显示出单一指标和综合指标模型在预测炉膛结渣情况时单独使用具有预测分辨率较低的局限性,因此需要综合考虑多项评判指标结果来确定最终结渣情况。

又对另外一台燃用石炭二选系烟煤的600 MW级亚临界锅炉机组以及两台分别燃用活鸡兔矿煤、兖矿煤与济北煤矿混煤的1 000 MW级超超临界锅炉机组进行了预测分析,上述3种煤种分别用A、B、C表示。表5、表6分别为煤种特性分析及锅炉参数数据和单一指标与多指标模型预测结果。

表3 煤质、灰分成分分析

注:Mt为煤的全水分。

表4 300 MW锅炉机组单一指标、多指标综合预测结果

由表6可知:8项评判指标对燃用A煤种的锅炉炉膛结渣情况预测结果均为轻微结渣,因此最终预测结果为轻微结渣;对燃用B煤种的锅炉机组预测结果中有6项为严重结渣,2项为中等结渣,因此最终预测结果为严重结渣;对燃用C煤种的锅炉机组8项预测结果中轻微和中等结渣各有4项,只能粗略判断该机组燃用该煤种时炉膛结渣情况为轻微或中等结渣。根据以上结果可知:单一指标和综合指标模型对不同煤种、不同炉型的分辨率有所不同,因此在选用合适的评判指标前,需进行比较分析,尽可能选用对燃用煤种和炉型分辨率较高的评判指标。

表5 煤种特性分析及锅炉参数数据

表6 600 MW、1 000 MW锅炉机组单一指标、多指标综合预测结果

2 基于模糊神经网络的炉膛结渣模型与预测

神经网络具有较强的自学习能力和并行处理能力,可解决非线性控制问题。在学习过程中,通过不断调整权值和阈值,使得网络逐步适应所学习数据,进而具有高度的容错性、适时性和鲁棒性,经适当训练的网络具有极强的泛化能力,即当出现训练中未出现的数据时仍能进行辨识,但神经网络不能处理结渣程度这类模糊问题。模糊系统虽很难实现自适应学习却擅长处理模糊信息。本文将模糊系统与神经网络相结合,使得两者都能发挥各自优势,将经隶属函数处理过的数据作为神经网络输入数据,并通过神经网络的学习为模糊系统提取模糊规则,从而解决结渣程度这一模糊问题[13]。

2.1 模糊神经网络结构

在考虑影响炉膛结渣情况的燃煤特性基础上,同时考虑锅炉运行方式等因素,因此该模糊神经网络的输入项分别为t2、RBA、RG、RSiAl、R、ψt(量纲一炉膛最高温度)6项,其中ψt的计算式如下

(5)

式中:Bj为计算燃料消耗量;Qd为煤的低位发热量;a、b为炉膛宽度、深度;ηf为二次风层数;Ca为二次风距;ξ为卫燃带修正系数

(6)

其中Fw为卫燃带面积,H为燃烧器高度。

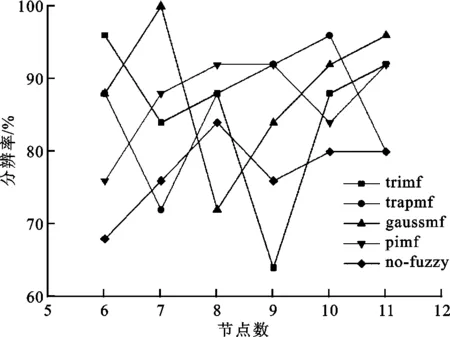
图1 不同节点数构造的神经网络学习精度

由于结渣程度本身是一个模糊的概念,利用不同隶属函数进行预判时存在一定偏差,本文利用三角形隶属函数(trimf)、梯形隶属函数(trapmf)、高斯型隶属函数(gussmf)以及π型隶属函数(pimf)分别对输入项进行模糊化处理。模糊层即第1隐层分别对应各输入项的3种结渣程度隶属度,共18个节点,将模糊后的数据作为神经网络输入项,第2隐层节点数分别为6～11时不同隶属函数构造的模糊神经网络以及传统神经网络(no-fuzzy)各自学习的分辨率如图1所示,在考虑网络精确度和结构简单的前提下,确定出不同隶属函数构造的模糊神经网络第2隐层节点数分别为6、10、7、8,传统神经网络隐层节点数为8。通过第1隐层与第2隐层、第2隐层与输出层之间权值、阈值的不断调整,得到输出项炉膛结渣程度(轻微、中等、严重),最后根据最大隶属度原则确定炉膛结渣程度预测值。本文所建立的模糊神经网络拓扑结构以pimf为例,如图2所示。采用BP神经网络算法,第1、2隐层间为tansig型传递函数,第2隐层与输出层间为logsig型传递函数,学习函数选用learngdm函数,训练函数选用trainlm函数。

图2 pimf模糊神经网络拓扑结构

各输入项隶属函数根据结渣倾向评判标准进行确定。t2、RBA、RG、RSiAl的评判标准如表1所示,R的评判标准如1.2小节所述,ψt≤0.97为轻微结渣,0.97<ψt<1.065为中等结渣,ψt≥1.065为严重结渣。例如,软化温度t2的π型隶属函数为

(轻微)

(中等)

(严重)

其余输入项的隶属函数确定方法同上。

2.2 实例计算及分析

以采集到的34组不同锅炉数据为基础[14],其中25组作为神经网络的学习数据,另外9组与前文所述300 MW锅炉数据以及表5中3组锅炉机组数据作为预测数据,分别利用4种模糊神经网络和传统神经网络进行学习与预测,传统神经网络直接将6项数据作为输入项,没有进行模糊化处理。表7、8分别为传统神经网络和4种模糊神经网络的学习、预测结果。

表7 传统神经网络、模糊神经网络学习结果

由表7结果计算可知:4种模糊神经网络学习结果都较好,分辨率依次为96%、96%、100%和92%,传统神经网络学习分辨率略低,为84%,以上网络都可以作为预测网络使用。由表8结果计算可知:传统神经网络分辨率约为62%,模糊神经网络分辨率依次为92%、92%、92%以及100%,表明模糊神经网络相对于传统神经网络有较高的分辨率。不同隶属函数构造的模糊神经网络存在一定偏差,虽然这里pimf构造的模糊神经网络预测结果为100%,但由于预测数据有限,无法确保该模型对所有数据都能达到100%的分辨率。于是,通过对多种隶属函数构造的模糊神经网络的计算结果进行统计,得到统计结果,其相对于单一模糊预测模型分辨率有了大幅提高,分辨率可以达到100%。采用统计结果这一指标对300 MW锅炉和另外3组锅炉机组的预测结果分别为严重结渣、轻微结渣、严重结渣、中等结渣,与实际结渣情况相符合,表明模糊神经网络相对于基于燃煤特性的单一指标和综合指标预测模型分辨率较高,有极强的泛化能力,对不同煤种及锅炉型号适用性更强。

表8 传统神经网络、模糊神经网络预测结果

据文献[15]可知,由于燃烧不均匀会使炉膛内不同位置结渣程度有所不同,炉膛结渣主要集中于燃烧器附近、卫燃带周围及折焰角等部位。这些部位烟气温度高、流动性差,更容易出现结渣现象,而基于燃煤特性的炉膛结渣预测模型和基于模糊神经网络的炉膛结渣预测模型均只能针对炉膛整体结渣情况进行预测,无法确定结渣具体位置。

3 基于污染系数的神经网络炉膛局部结渣模型与在线预测

3.1 灰污特征参数的选取

对于炉膛结渣情况的监测,常用热有效系数Ψ、基于炉膛出口烟温的污染系数ξ和基于换热量的污染系数Γ进行监测。其中,热有效系数可以准确反映水冷壁上沾污、结渣程度,当污染严重时,水冷壁的热有效系数减小,但是炉膛火炬投射热流很难测得。炉膛出口烟温也能综合反映炉膛结渣状态,当炉膛结渣严重时,水冷壁吸热量减少,炉膛出口烟温升高。目前常用两种方法获取炉膛出口烟温:一种是利用热平衡法根据各受热面汽水温度反推炉膛出口烟温,但该方法误差较大;另一种是利用热电偶、红外测温仪等设备直接测量,虽准确性高于前者,但由于设备庞大且难以长时间在炉膛高温烟气环境下工作或因过于昂贵而难以推广。本文通过在水冷壁背面安装两个温度测点,建立温度与热流密度间的关系,从而得到测点处热流密度,利用污染系数φ实现对炉膛结渣情况进行局部监测。φ的值在0～1之间,其值越接近于1,表明炉膛结渣越严重,φr为其真实值,φp为其预测值,φ的计算式为

(7)

式中:qsj为水冷壁实际热流密度;qlx为炉膛清洁时的理想热流密度。

3.2 实际热流密度

文献[16]给出了膜式水冷壁温度场的近似解析解,据此可通过水冷壁壁面温度与热流密度间的关系求得炉膛实际局部热流密度。图3为膜式水冷壁结构图,其中C、E为温度测点[16],管子部分温度场的近似解为

(8)

式中:tp为管内介质温度;q0为炉膛辐射热负荷;λ为管壁导热系数;φ0=S/2πr1,S为管子节距;β=r1/r2,r1、r2分别为管子外径、内径;z=r/r1,r为所求点到圆心的距离;φn据φn/n线算图查得;Bn=β-2n(n-Bi)/(n+Bi),Bi=r2α2/λ,α2为管内壁对工质的放热系数;θ为r与y轴正方向的夹角。

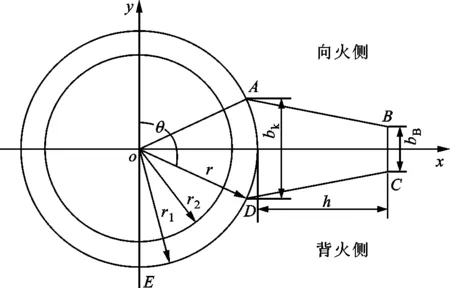
图3 膜式水冷壁结构图

梯形鳍片部分温度场的近似解为

(9)

矩形鳍片部分温度场的近似解为

(10)

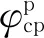
本文所述300 MW锅炉为矩形鳍片,根据式(11)～(13)可知,如果测点C、E温度已知,则只剩下q0未知,由于α2很难测得,故也为未知量,C、D、E点的温度分别为

(11)

(12)

(13)

由式(11)～(13)可分别得到关于q0的方程式,然后联立可得

(14)

式(14)中有一个级数求和问题,据文献[12]中φn/n线算图可知,对于非错位鳍片管,当S/D=1.25、n=8时,φn/n取0.008已经很接近于0,因此取n=8即可满足工程需要。由于D、E两点位于管外径上,z=1,将Bi、Bn分别代入,经化简,式(14)可近似为

(15)

式(15)中未知量只有一个α2,求得该方程解之后,代入式(13)可求得q0,该处实际热流密度qsj=q0。

3.3 理想热流密度

根据3.2小节的分析可知,根据现场测量的C、E两点温度可以求得该处实际热流密度qsj,但对应工况下的理想热流密度qlx无法通过测量求得,神经网络可以解决这一问题。将吹灰后各运行工况下的热流密度作为清洁热流密度,以此作为神经网络训练数据进行训练从而得到训练好的神经网络,由于神经网络具有极强的泛化能力,实际工况对应下的理想热流密度便可以利用训练好的神经网络预测得到,最后根据式(7)即可得到各工况所对应的污染系数φ。

影响炉膛结渣的因素包括煤质特性、锅炉结构以及运行参数,基于燃煤特性的炉膛结渣预测模型都是根据煤质特性进行煤质结渣倾向预判,但是炉膛是否结渣不仅仅只是取决于煤质特性,因此上述方法存在一定的不准确性。锅炉结构影响结渣的程度主要体现在锅炉设计之初为避免结渣而进行的一些相关设计上,不过锅炉结构与其他因素也会由于相互作用而影响结渣程度。运行参数对炉膛结渣影响最大,本文在综合考虑这3个影响因素的基础上来确定神经网络的输入项。

将影响清洁水冷壁热流密度的因素作为神经网络的输入项,包括主蒸汽流量、氧量、MF1层给煤量、MF2层给煤量以及MF3层给煤量,水冷壁清洁时的热流密度作为输出项。经多次训练比较,隐层节点数确定为7。采用BP神经网络算法,输入层与隐层间为tansig型传递函数,隐层与输出层间为logsig型传递函数,学习函数选用learngdm函数,训练函数选用trainlm函数。

3.4 实例计算及分析

首先利用吹灰后主蒸汽流量,氧量,MF1层、MF2层、MF3层给煤量,以及测量并计算得到的理想热流密度对神经网络进行训练,得到训练良好的神经网络,接着从DCS数据库中提取各实际运行工况下的5项输入项,经神经网络测试得到各工况下的理想热流密度,再根据式(7)得到相应的污染系数。

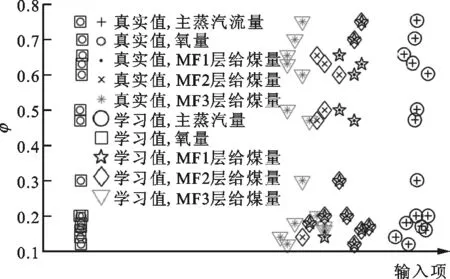
图4 神经网络学习结果

图5 神经网络预测结果

图4、图5分别为神经网络对污染系数的学习结果和预测结果。根据图4可知:真实值与学习值吻合很好,因此该神经网络可以用于预测炉膛局部结渣情况。图5中斜线代表预测值与真实值相等,圆圈越靠近直线表示预测值与真实值越相近。根据图5可知:该神经网络预测误差在3%以内,均方误差为0.013 4,因此该神经网络具备较高的可信度,可以较好地对炉膛局部结渣情况进行实时监测。图6为污染系数随时间的变化图,由图可知,在40～80 min时污染系数出现急剧下降,此时正进行吹灰操作,炉膛污染系数急剧减小,与实际情况相符合,说明该神经网络可以用于反映炉膛局部结渣情况,并用于指导炉膛吹灰。

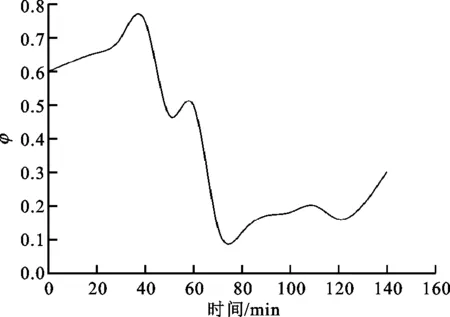
图6 污染系数随时间的变化图

4 结 论

(1)基于燃煤特性的单一指标和综合指标预测模型可以在一定程度上对炉膛结渣情况进行预测,但其分辨率较低,且往往对于不同煤种或不同炉型分辨率也不同;从预测结渣范围上看,该模型只能对炉膛整体结渣情况进行监测。

(2)基于模糊神经网络的炉膛结渣预测模型将神经网络极强的学习能力与模糊算法的处理模糊知识能力相结合,同时引进炉膛结构参数,相对于仅有燃煤特性参数的单一指标和综合指标方法及传统神经网络的分辨率均有了显著提高,4种模糊神经网络的分辨率可分别达92%、92%、92%以及100%,针对模糊神经网络的统计结果分辨率也可达到100%;虽然模糊神经网络对不同煤种及炉型适用性更强,但也只能对炉膛整体结渣情况进行预测。

(3)基于污染系数的神经网络炉膛结渣在线预测模型可实现对炉膛局部结渣情况的实时预测,且误差在3%以内,均方误差为0.013 4,可用于电站指导炉膛吹灰。