高液面共振圆柱形混合容器中的表面波特性
庞琳佳,王小鹏,陈松,奚延辉
(1.西安交通大学机械工程学院,710049,西安;2.西安近代化学研究所氟氮化工资源高效开发与利用国家重点实验室,710065,西安)
当装有液体的圆柱形刚性容器底部有一垂直振动激励时,在自由液面上会形成非线性表面驻波,这就是法拉第波现象[1]。法拉第波的不稳定性问题是当今流体力学中不稳定性问题之一,此类波动问题具有重要的工程背景和理论意义,法拉第波的条纹、方形、五边形、六边形等各种模态相继被发现[2-8]。
法拉第指出,这种表面波的频率是垂直激励频率的一半,随后Rayleigh做了一系列相关实验,验证了法拉第关于表面波频率的观点,但未给出数学上的解释[9]。1954年,Benjanmin等从理想流体出发,将边界条件线性化并考虑了表面张力的影响,得到了描述自由表面运动的Mathieu方程,并用稳定性理论证实了法拉第的结论[10]。但是,目前大多数学者对法拉第表面波的研究主要集中在频率小于20 Hz、液面低于5 mm的阶段,对于频率在60 Hz左右、液面较深的法拉第波并未见相关的报道。
超细材料已广泛应用于航空航天、国防军工、生物工程、机械、电子等领域。超细材料的关键指标是其在基体中的分散混合均匀性,而传统超细材料分散混合技术通过较大的剪切力、挤压力或局部空蚀作用打开超细材料的团聚来实现分散,此过程会对材料产生较大的应力刺激,伴随较强的生热过程,因此提出一种新型分散技术。共振混合是一种新型低频混合技术[11-13],通过混合容器外部激励使容器内混合物产生密度差异和能量梯度,造成混合物大范围内的对流共同作用,达到分散混合的目的,该方法是一种无浆混合技术,避免了被混物料与桨叶、螺杆等元件的局部强烈剪切和摩擦,大大降低了混合过程的力刺激和热刺激[14]。
综上所述,本文主要针对共振混合容器中较高激振频率、较高液面的法拉第表面波波动进行研究。以水波波动为基础,建立混合容器数学模型,探究在各参数激励下混合容器中所激发的表面波模式及非线性特性关系。
1 理论分析
1.1 运动控制方程
本文所研究共振混合容器中的波为水表面波,即在初始扰动后,其恢复力是重力。在共振混合实验中,底部激振器垂直振动,通过支架、弹簧组、负载板等力的传递,给混合容器底部施加一个垂直激励,机械能作为输入能,水波作为输出能。若混合容器为圆柱形,可将混合容器简化为数学模型,如图1所示,图中容器半径为R,液面高度为h,容器底部受到垂直方向的激振力F=Acos(2w0t)。
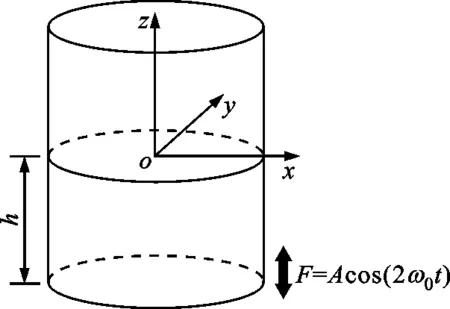
图1 混合容器简化模型
假设圆柱形内液体无黏且不可压缩,同时满足连续性方程[15],即
·u=0
(1)
式中:u为空间点(x,y,z)处t时刻的流体速度。假定流体是无旋的,即有
×u=0
(2)
在柱坐标系(r,θ,t)下,以运动容器为参考系,将自由液面作为平面z=0,于是存在速度势函数φ,有u=φ,代入式(1)可得[16]
2φ=0-h (3) (4) 式中g为重力加速度。 对平底流场,假设底部不可渗透、无黏性,底面上各点线速度为0,可得边界条件 φz=0;z=-h (5) φr=0;r=R (6) 将式(6)在z=0点泰勒展开,原方程可化为 (7) 边界条件 (8) (9) (10) (11) 式中:ε为与驱动振幅有关的小参量,ε远远小于1。 水波问题是带有非线性边界条件的不定边界问题,通常采用数学物理方程中的摄动方法,把水波问题的解按照某个小参量用渐近级数展开,一阶近似的解即为小振幅波(Airy波)[17]。这个小参量可设为波高与波长之比,小振幅波的振幅和速度都是最小量,其压力由静水压力和动压力组成。本文借鉴文献[18],利用摄动展开法,引入慢变时间尺度τ,令τ=ε2t,将方程的解按照小参量ε做摄动展开,对控制方程及式(7)~(11)进行求解,得速度势和自由面位移的表达式 φ(r,θ,z,t,τ)=εφ1+ε2φ2 (12) η(r,θ)=εη1+ε2η2 (13) Ω2=gλmntanh(λmnh) (14) 式中:φ1、φ2分别为速度势函数一阶解、二阶解;η1、η2分别为自由面位移一阶解、二阶解;Ω为表面波的自然频率。 求得自由面位移波动方程后,本文将对不同驱动频率与不同时段下混合容器内自由液面处表面波模式进行数值模拟分析。 在某一特定参数激励条件下,混合容器内自由液面处会形成各式各样的波纹,称为表面波(m,n)模式。所谓(m,n)模式是指在坐标区域为(-1,1)内,沿圆周方向分别有m个波峰和m个波谷,即沿直径方向共有m条通过原点的对角线,沿半径方向有(n-1)个波节环。 (1)表面波(8,4)模式。混合容器材料为PMMA有机玻璃,容器直径为90 mm,高度为100 mm。若混合容器内液面高度为7 cm,当驱动频率为36 Hz、加速度为10g时,通过计算可知混合容器振动幅值为1.9 mm,且混合容器内自由液面处所激发的表面波为(8,4)模式,数值模拟图如图2所示。计算过程采用柱坐标系x=rcosθ、y=rsinθ,分别沿半径方向分布;深色区域表示在该位置处位移高于自由液面,浅色区域表示在该位置处位移低于自由液面,并且深色区域越深表示高出自由液面的差值就越大,浅色区域越深表示低于自由液面的差值就越大。表面波俯视图如图2a所示,在区间(-1,1)内,沿圆周方向分别有8个波峰和8个波谷,即沿直径方向共有8条通过原点的对角线,沿半径方向有3个波节环。由图2a可知,越靠近激振中心的位置,自由面位移就越大,离激振中心越远,自由面位移就越小。(8,4)模式下单一相邻波峰波谷图如图2b所示,0位置表示混合容器自由液面处,深色区域代表表面波的波峰,浅色区域代表表面波的波谷。 (a)表面波俯视图 (b)波峰波谷图图2 表面波(8,4)模式模拟图 (2)表面波(7,6)模式。在共振混合容器相同条件下,若驱动频率为52 Hz、加速度为10g,混合容器内的液面高度为7 cm,通过计算可得混合容器振动幅值为0.9 mm,混合容器内所激发的表面波为(7,6)模式。混合容器表面波(7,6)模式数值模拟图如图3所示。沿圆周方向分别有7个波峰和7个波谷,沿半径方向有5个波节环。同一半径方向上,越靠近激振中心的位置自由面位移越大,远离激振中心的位置自由面位移越小。 (a)表面波俯视图 (b)波峰波谷图图3 表面波(7,6)模式模拟图 对比图3、图4可知,通过数值计算,在给定的溶液、容器、加速度的条件下,频率增大所激发的表面波模式变得相对复杂。水波中每个质点的运动都是纵向和横向运动合成的,靠近激振中心振幅最大,说明此处水波质点运动剧烈,远离激振中心振幅逐渐减小,说明水波质点运动逐渐减弱,这一变化过程体现出水波固有的扩散性与衰减性。此外,(7,6)模式所激发出的波高(相邻波峰波谷距自由面位移之和)大于(8,4)模式下所激发出的波高,这是由激振频率大小引起的。由于自由面表面波函数是一个奇函数,因此根据法拉第表面波函数的奇异性,在表面波等高线图的数值结果中中间区域为空,即表面波在圆柱容器轴线上振幅为0。 为探究不同时间段内表面波的变化情况,对表面波(7,6)模式进行研究,通过对时间段4.163~4.168 ms内混合容器内表面波进行数值模拟,以此揭示水波的运动特征。 不同时段下表面波模式如图4所示,可知在同一圆周上各位置处振幅大小不同,在同一半径上各位置处振幅大小也各不相同,各时间点、各位置处振幅大小不一致。图4a中近圆心处与远离圆心处振幅差值不大,浅色区域表示该位置处振幅最大,深色区域表明振幅最小;图4b中最大振幅处与最小振幅处差值显著,波纹明显增加,激振中心不同位置处振幅最大值与最小值交错排列;图4c中在同一圆周上各位置处振幅大小均相等且在同一半径上,越靠近激振中心的位置处振幅越大,越远离激振中心的位置处振幅越小,颜色均匀分布,波纹分布明显且排列整齐,表明这一时刻(7,6)模式被完全激发出来。随着时间的推移,图4d中同一圆周处振幅大小不一致,振幅最大处与振幅最小处发生位置互换,颜色开始发生不均匀现象,右上角浅色区域表示该位置处振幅最大,右下角深色区域表示振幅最小,颜色分布与图4b发生位置互换。图4e颜色较图4d的明显变浅,且波纹减少,右上角区域振幅最大,右下角区域振幅最小,与图4a发生了位置互换。 轴向展开图 表面波俯视图(a)t=4.163 ms 轴向展开图 表面波俯视图(b)t=4.166 2 ms 轴向展开图 表面波俯视图(c)t=4.166 52 ms 轴向展开图 表面波俯视图(d)t=4.167 ms 轴向展开图 表面波俯视图(e)t=4.168 ms图4 不同时段下表面波模式 由图4可知,共振混合容器中法拉第表面波的变化与时间紧密相关。在某一时间段内,随着时间的推移,表面波(7,6)模式在某一时间点处完全出现,随后逐渐消散,振幅最大处与振幅最小处发生位置变化,说明在模式完全出现前后,水波波峰、波谷位置不断变化,且表面条纹图案也发生变化。这一过程表明受底部激励的混合容器内水波质点发生一维方向上的迁移,随着激励振幅大小的变化而不断变化,揭示了水波运动的不稳定性。 时空混沌(STC)是指在同时具有空间和时间自由度的时空系统中表现出时间混沌而空间不规则的运动行为,在参数强迫的表面波中表现为无序波动域与水波条纹共存的现象[19]。与STC相关现象包括时空间歇性、时间平均模式的空间周期性和横向振幅调制。本文对短时间内表面波(7,6)模式时空混沌现象进行了研究。 (a)t=0.12 s (b)t=0.15 s (c)t=0.17 s图5 时空混沌现象 时空混沌现象如图5所示,由共振混合容器参数不稳定引起的法拉第表面波,在短时间内快速失稳导致STC的出现。由图5可知:时间从0.12 s到0.17 s的过程中,混合状态下条纹区域会受到振荡不稳定性的扭曲,混合容器中心产生的奇异点处,表面波波纹较明显;随着时间的推移,从奇异点处开始延伸到容器边界处的波纹慢慢减少,这说明容器边界同心圆区域处开始出现时空混沌现象,导致数值仿真结果中表面波波纹函数在容器边界处无法体现。此外,不同时间节点下所对应的颜色不同,表示波动位移值也在随着时间的变化而变化,表明在参数强迫表面波过程中,体现了强烈的时空混沌和层流条纹共存的一种状态。 本文对共振混合容器中自由液面处表面波动情况进行了研究,通过简化混合容器边界条件,建立了混合容器模型与数学表达式,通过方程求解并对自由液面处水波进行数值模拟,研究了不同参数下水波变化与运动特性,对今后研究混合容器内法拉第波对液体混合的影响具有指导意义。 (1)本文基于激振频率对法拉第表面水波的影响进行了研究,发现混合容器半径与液面高度不变的情况下,表面波模式随着频率的增大而变得复杂。自由面表面波函数是一个奇函数,因此表面波在圆柱容器轴线上振幅为0,这种现象与数学上法拉第表面波波动的奇异性一致。 (2)通过对(7,6)模式下不同时段内表面波进行探究,表明混合容器中法拉第表面波的波动变化与时间有关。变化过程中数值模拟可得:振幅最大处与振幅最小处发生位置变化,且表面条纹图案发生变化,说明混合容器内水波质点在一维方向上发生迁移,证明了水波波动的不稳定性。 (3)通过对(7,6)模式下时空混沌现象进行研究,可得STC现象最开始发生在容器边界处,并缓慢向奇异中心点延伸,混合容器参数不稳定性会引起时空混沌与表面波条纹共存的现象。1.2 表面波非线性解
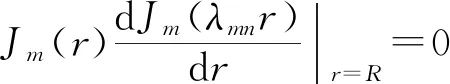
2 共振混合容器中的表面波特性
2.1 不同驱动频率下表面波模式


2.2 不同时段下模式变化图





3 时空混沌现象


4 结 论

