发展空间观念 落实核心素养助推专业成长

何景龙

“三角形的认识”是人教版小学数学四年级下册，第五单元“三角形”中三角形的特性第60页～61页三角形的认识例1。以发展空间观念来指导、设计和执教本节课，有利于落实核心素养，助推小学数学教师专业成长。空间观念是《数学课程标准（2011年版）》10大核心概念“数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识”之一。《数学课程标准（2011年版）》从四个方面对空间观念进行了刻画和描述：根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体；想象出物体的方位和相互之间的位置关系；描述图形的位置和变化；依据语言的描述画出图形等。据此设计和执教的“三角形的认识”这节课较好地体现了发展空间观念，落实核心素养，助推专业成长，具体如下：

1.概念的引入环节从实物上来，再到实物上去。由三角形实物抽象概括出几何图形三角形，再到由几何图形三角形联想想象出三角形实物，发展了学生的空间观念，将学科核心素养，落实在实际的具体学科课堂教学之中。

“三角形的认识”属于概念教学。概念是人们对客观事物的一种抽象概括，抽象概括时要明确概念的内涵和外延，给概念下定义就是揭示概念的内涵或外延。揭示内涵的定义叫做内涵定义，揭示外延的定义叫做外延定义。任何定义都是由被定义项、定义项和定义联项3部分组成，被定义项是需要明确的概念，定义项是用来明确被定义项的概念，定义联项是用来联接被定义项和定义项的。比如本节课“由3条线段围成的图形（每相邻两条线段的端点相连）叫做三角形”。其中的“三角形”是被定义项。“由3条线段围成的图形（每相邻两条线段的端点相连）”是定义项，“叫做”是定义联项。采用的是内涵定义中的发生式定义法，此法也称构造性定义法，通过被定义概念的发生过程，形成的特征的描述来揭示被定义概念的本质属性。本节课，上课伊始，学生通过观察埃及金字塔、南通长江大桥（见下图）等图片的共同特征，从三角形实物上抽象概括出所要学习的三角形几何图形。

再让学生画出一个自己喜欢的几何图形三角形，然后由其他学生通过他所画的几何图形三角形来猜一猜是什么三角形实物，体现了从实物上来，再到实物上去，由抽象概括到联想想象，发展了小学生的空间观念，将学科核心素养落实在实际的具体学科课堂教学之中。见下图：

2.三角形“高”概念的认识建立在生活之上，又高于生活。充分利用了学生生活中对于“高”的原始的认识来发展他们的空间观念。

“三角形的认识”这节课有两个知识点，一个知识点什么是三角形，另一个知识点什么是三角形的高。特别是三角形的高不仅是本节课的重点，还是本节课的一个难点。在认识三角形的高时，本节课分为以下几个层次：

第一层次，三角形实物比高，如下图：

通过不同的摆放方向，充分地感知三角形实物的高，调动和激发了学生生活中对于“高”的原始的认识，即高是“上下”方向的，是垂直于水平方向的，这是学生的原有认知。借助学生原有的认知，通过三角形实物的3次比高，渗透了一个三角形图形有3条高，这是三角形高的第一层次的认识，为下一步抽象出三角形的高夯实了基础。

第二层次，从三角形实物上抽象出三角形，如下图：

此时由于三角形实物比高的影响，学生会很快地在三角形BCD图形上找到三角形的高，并且把它表示出来。然后再让学生用语言把三角形的高表述出来，从实物，到图形，再到语言描述一气呵成，使學生对三角形的高有了一个初步的认识，为后续的进一步理解三角形的高夯实了基础。

第三层次，通过旋转三角形，进一步加深对三角形高的认识和理解。如下图1：

同时提出两个问题：这时三角形DBC的高在哪里？线段BE还是三角形DBC的高吗？两个问题角度不同，层次不同。第一个问题既顺应了学生的原有认知，又巩固了学生对于三角形高的第一个层次的认识。第二个问题制造了认知冲突，线段BE不再是“上下”方向的了，也不与水平线垂直了，这时线段BE还是不是三角形DBC的高，这是一个关键的问题。通过学生的争论和辩论，实现了学生对于三角形高的认识，从量变到质变的飞跃，使学生明确虽然线段BE不再是“上下”方向的了，也不与水平线垂直了，但是线段BE还是与底边CD垂直，所以线段BE还是三角形DBC的高，跳出了只有线段DF才是三角形DBC的高的第一层次的认识，如图2。这样学生就会知道线段CH也是三角形DBC的高，如图3。从而知道了一个三角形可以有3条高，三角形的高不仅局限于“上下”方向，而是任意方向都可以，关键要看三角形的顶点和对边在哪里，为后续给不同的三角形画高夯实了基础。

三个层次体现了从生活到数学，从常规到变式，特别是三角形的旋转变化后再来找三角形的高，不仅有利于学生对于三角形的高的认识，而且还发展了学生的空间观念，三角形的高只与顶点和对边有关系，而与方向没有关系，无论是上下，还是左右，或者是其他任何一个方向。

3.沟通二维和三维之间的联系，将二维几何图形三角形放到三维空间来认识，进一步凸显三角形是平面图形，在三维空间来找三角形，不仅有利于学生对于三角形的认识，更有利于发展学生的空间观念。

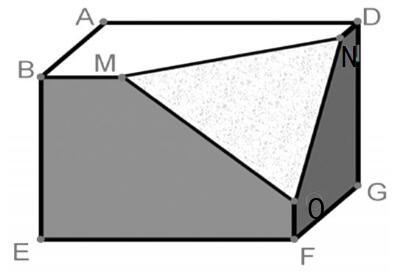
本节课的结尾匠心独具，通过在长方体上找三角形，如下图：

请你来说一说，在图上你能找到三角形吗？你所找到的三角形在哪里？请你来指一指。比如ΔMOC在BEFC面上，ΔCON在CFGD面上，ΔMNC在ABCD面上，当学生找到ΔMON时，却不知道这个三角形在哪里，课件演示如下图：

这时学生就会看到ΔMON本身就是一个平面，从而更加深刻地理解了三角形是一个平面图形。再让学生找下面的长方体上的三角形时，学生就会轻而易举地找到，并且知道所找到的三角形在哪里了。

空间观念的发展要日积月累，要渗透在具体的小学数学课堂教学之中。“三角形的认识”这节课进行了一个很好的尝试和探索，它不仅对于发展学生的空间观念大有好处，同时对于落实数学学科核心素养也大有好处，它不仅对于提升小学数学课堂教学水平大有好处，同时对于促进小学数学教师专业发展也大有好处。

本文系黑龙江省教育科学规划“十三·五”重点课题《小学生数学核心素养评价研究》（课题编号：JJB1316037）的子课题研究成果之一。本文的现场教学荣获2017年4月26日——28日在吉林省延吉市召开的“东北、华北人教版全国小学数学教学成果展示暨培训会”一等奖。

编辑/魏继军