立体图形变变变
孟泰
代数中经常要进行“平方”“换元”“去分母”等各种代数变换,在几何体中同样也需要“变换”,常见的变换有:平移、旋转、作截面、侧面展开、割补、翻折、压缩(如果选修了3-3《球面上的几何》,就会知道还有进行连续变形的所谓“拓扑变换”).
在定义几何体时,课本中(苏教版必修2,以下同)采用了如下变换技巧:
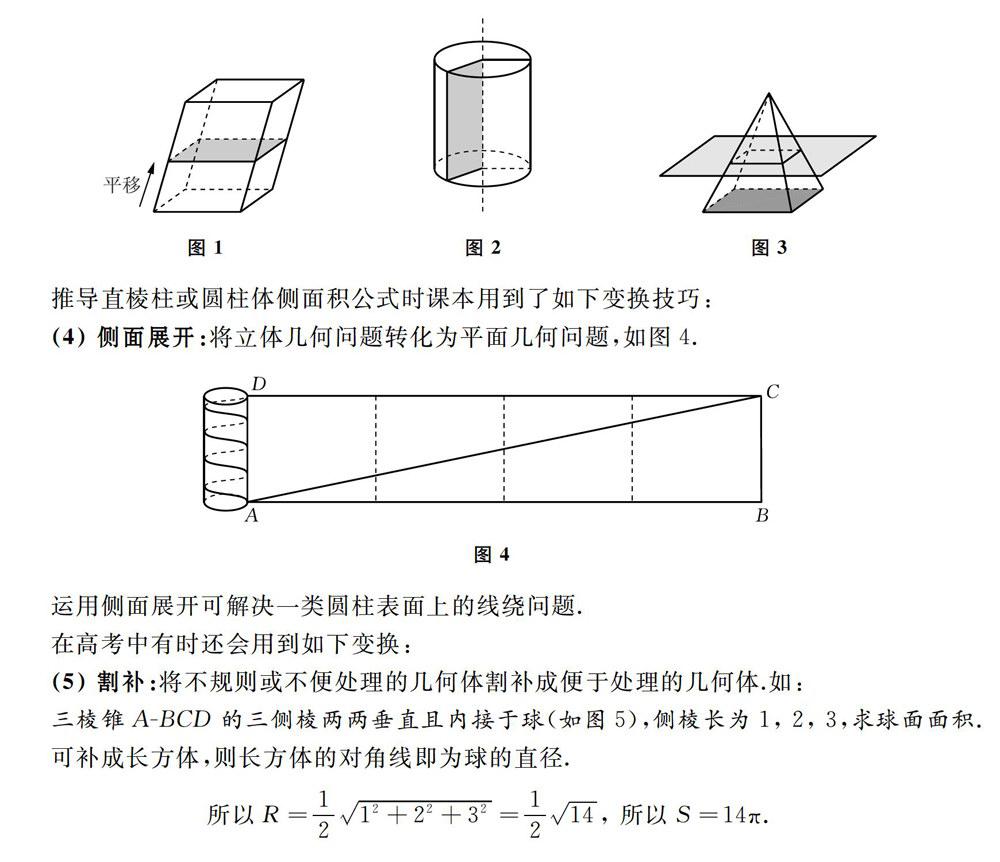
(1)平移:将多边形沿某一方向平移可得棱柱,如图1.
(2)旋转:将平面曲线绕某一直线旋转可得旋转体,如图2.
(3)作截面:将锥体作平行于底的一截面可得台体,如图3.推导直棱柱或圆柱体侧面积公式时课本用到了如下变换技巧:
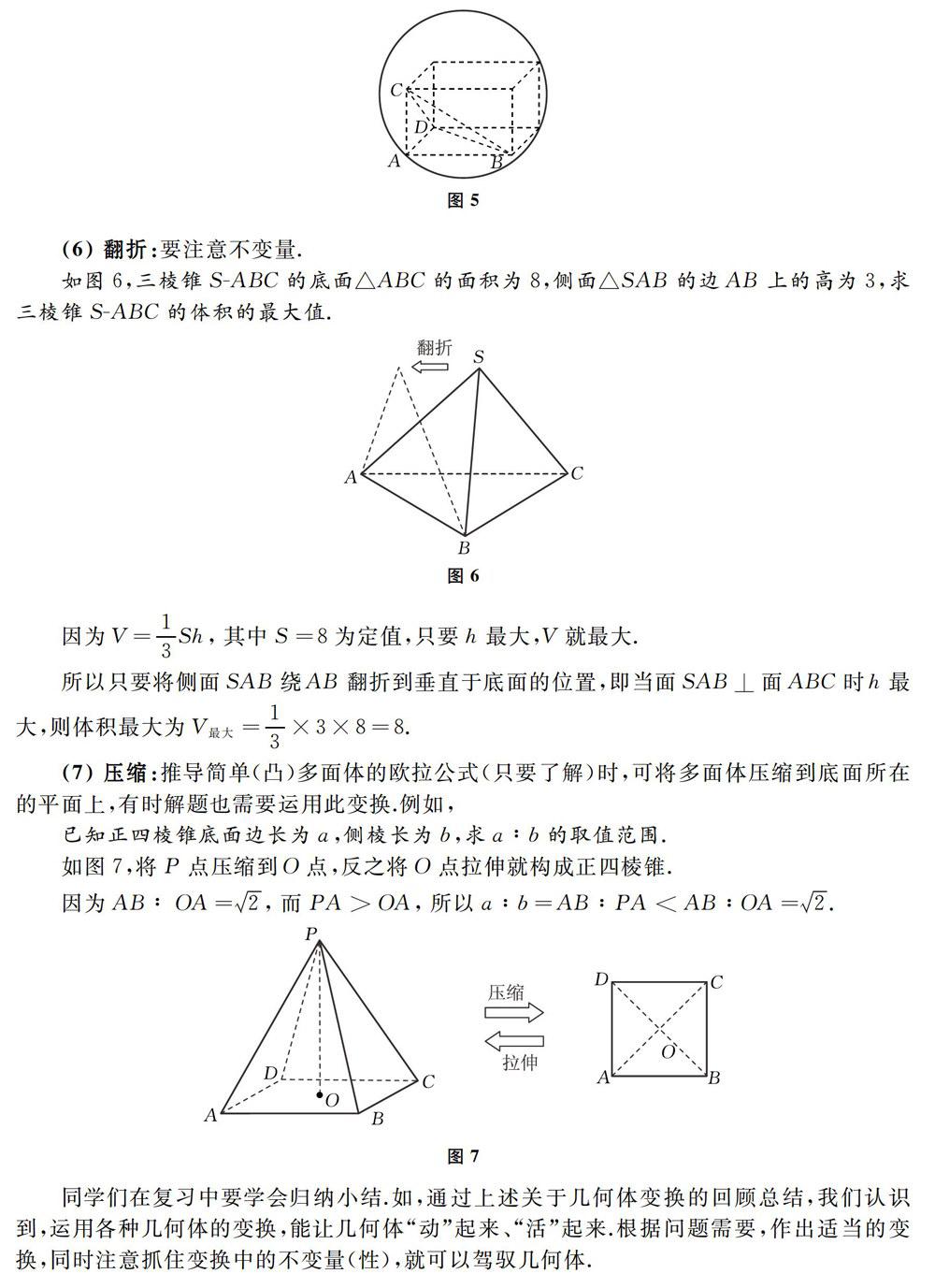
(4)侧面展开:将立体几何问题转化为平面几何问题,如图4.运用侧面展开可解决一类圆柱表面上的线绕问题,在高考中有时还会用到如下变换:
(5)割补:将不规则或不便处理的几何体割补成便于处理的几何体.如:三棱锥A-BCD的三侧棱两两垂直且内接于球(如图5),侧棱长为1,2,3,求球面面积.可补成长方体,则长方体的对角线即为球的直径.所以R=1/2√(1+4+9)=1/214√,所以s=14π,
(6)翻折:要注意不变量.
如图6,三棱锥S-ABC的底面△ABC的面积为8,侧面△SAB的边AB上的高为3,求三棱锥S-ABC的体积的最大值.
因为V=1/3Sh,其中s=8为窟值,只要h最大,V就最大,
所以只要将侧面SAB绕AB翻折到垂直于底面的位置,即当面SAB上面ABC时h最大,則体积最大为V最大=1/3××8=8.
(7)压缩:推导简单(凸)多面体的欧拉公式(只要了解)时,可将多面体压缩到底面所在的平面上,有时解题也需要运用此变换.例如,
已知正四棱锥底面边长为a,侧棱长为b,求a:b的取值范围.
如图7,将P点压缩到0点,反之将0点拉伸就构成正四棱锥,
因为AB:OA=√2,而PA>OA,所以以:b=AB:PA 同学们在复习中要学会归纳小结.如,通过上述关于几何体变换的回顾总结,我们认识到,运用各种几何体的变换,能让几何体“动”起来、“活”起来.根据问题需要,作出适当的变换,同时注意抓住变换中的不变量(性),就可以驾驭几何体.

