基于概率信息不完备的群决策模型
戴意瑜,陈 江
(华侨大学 信息化建设与管理处,福建 厦门 361021)(*通信作者电子邮箱daiyy@hqu.edu.cn)
0 引言
区块链(Blockchain)是比特币的底层技术,这项技术因其安全、便捷的特性逐渐得到了银行与金融业的关注。区块链目前主要分为三类:公有区块链、联合(行业)区块链以及私有区块链[1-2]。区块链管理对区块链的发展有着重要保障,区块链管理中的一个重要课题是区块链类型的选择。事实上,从某种程度上看,区块链的选择问题其实是一个群决策问题。在现实多属性决策过程中,由于现实世界的复杂性和决策过程中主客观因素的影响,使得决策者在对决策方案相对于属性指标进行评估时,更加倾向于运用模糊信息表达评估值。模糊集[3]通过特定的数学符号工具描述真实信息的模糊性和不确定性,已成功地应用于许多领域,如模糊决策[4]、模糊控制[5]、模糊偏好[6]、模糊聚类[7]以及模糊粒度计算[8]。同时,为了满足实际决策需求,模糊集已经扩展为不同的形式,包括区间值模糊集[9]、多重模糊集[10]、直觉模糊集[11]、区间直觉模糊集[12-13]和犹豫模糊集[14]等。
由于犹豫模糊集(Hesitant Fuzzy Set, HFS)可以表达隶属度的所有可能信息,因此针对犹豫模糊偏好关系的研究越来越受到人们的关注。犹豫模糊偏好关系的一致性方法和方案的排序权重计算方法一直是犹豫模糊偏好关系的两个重要研究方法。Zhou等[15]基于概率犹豫模糊集设计了一种全新的决策方法,提出了犹豫风险值和期望犹豫风险值,用于处理尾部风险决策问题。针对群推荐中存在的多粒度、犹豫性、模糊性语言信息问题,陈秀明等[16]提出多粒度犹豫模糊语言环境下未知权重的多属性群推荐方法。Liao等[17]建立了一种犹豫模糊语言方法用以处理属性间存在冲突的决策问题。Wei等[18]基于犹豫模糊语言术语集得分函数提出了新的犹豫模糊语言方法。在犹豫模糊语言环境下,文献[19]建立了新的对犹豫模糊语言元进行完全排序的关系系统。
但是,HFS中元素的发生概率是相等的,这显然是不足的。例如当10位专家同时对一辆汽车进行评价时,其中8个专家提供的偏好为0.7,另外2个专家提供的偏好为0.2。然而运用HFS表示上述信息为{0.7,0.2},这只能反映专家们提供了哪些偏好信息,显然丢失了元素发生的概率。于是Zhang等[20]将概率引入到犹豫模糊集中,提出了概率犹豫模糊集的概念,并给出了其运算法则。但是在概率犹豫模糊集的实际应用中,决策者可能难以准确和充分地提供元素的发生概率。例如,一个专家利用犹豫模糊元素{0.4,0.7,0.9}描述一辆汽车的安全性能,这位专家认为安全水平是0.9的程度确定的,它的发生概率可以设定为0.2,而安全水平分别为0.7和0.4的发生概率是不确定的。在这种情况下,需要一种能够表达不完备概率信息的工具。在不同模糊信息环境下研究群决策问题,已受到了国内外学者的广泛关注和研究。关于区块链选择问题的研究是一个新兴的研究课题,相关的研究成果寥寥无几,因此,有必要研究运用更符合实际的概率不完备犹豫模糊偏好关系处理区块链选择问题,并设计相关的一致性改进算法和相容性实现模型。于是,本文引入了概率不完备犹豫模糊偏好关系等概念,并且构建最优化模型计算不完备犹豫模糊偏好关系中缺乏的概率信息,最后建立了基于群体一致性调整算法的决策模型,同时将建立的模型应用于实际案例中。
1 相关概念
本章首先给出犹豫模糊偏好关系的定义,然后针对犹豫模糊元中元素发生的概率信息是否已知或部分已知的情形,引入概率不完备犹豫模糊偏好关系的概念。


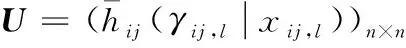
1)γji,l=1-γij,l,xji,l=xij,l且#hij=#hji。


接下来,引入概率不完备犹豫模糊偏好关系的期望一致性定义。
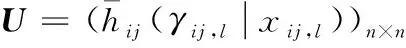
(1)

然而在复杂的现实决策过程中,专家们很难都提供具有完全一致性的PIHFPR,即式(1)通常是不成立的,因此定义如下满意期望一致性概念。
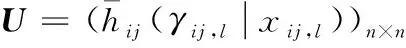
(2)
则称U具有满意加性期望一致性。
2 PIHFPR中元素发生概率确定模型
对于给定的PIHFPR,如何确定概率不完备犹豫模糊元中每个元素发生的概率是一个重要的研究课题。为了解决这个问题,本文的目标是使得获得的元素发生概率能够尽可能地提高PIHFPR的一致性,即式(1)两端的偏差尽可能小,于是以式(1)两端偏差为目标函数,构建如下最优化模型:
(3)
i,j=1,2,…,n
为了将上面的非线性最优化模型转化为更容易处理的线性最优化模型,本文引入两个偏差变量,即:

(4)
求解上述线性最优化模型(4),即可得到概率不完备犹豫模糊元中每个元素发生的概率。
3 基于PIHFPR的群决策模型
3.1 综合PIHFPR的集成方法

U0=q1U1⨁q2U2
(5)
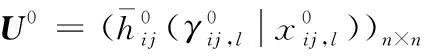


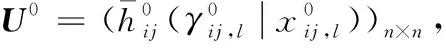

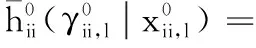
{0.5|1}
另一方面,因为

那么
(6)
而
(7)
证毕。
下面介绍群体PIHFPR集结成一个综合PIHFPR的方法。

U=q1U1⨁q2U2⨁…⨁qKUK
(8)
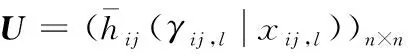


3.2 概率信息不完备的群决策模型

(9)
如果CIk≤ξ0,则转到步骤4;否则,执行步骤3。
(10)
(11)
如果CI≤ξ0,则执行下一步;否则,重复运用步骤1~3中的方法对一致性进行改进,直到CI≤ξ0为止。
步骤7 根据方案排序权重wi(i∈N)对悲观方案进行排序,选择综合表现最优的备选方案。
4 算例分析
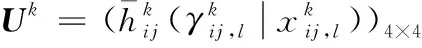
取一致性指数阈值ξ0=0.05。运用本文提出的群决策模型处理上述问题,具体步骤如下:





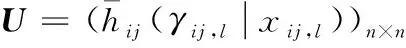
为了说明本文方法的有效性,运用文献[21]中的决策方法处理上述问题,大致步骤如下。
首先,基于三个PIHFPRUk(k=1,2,3),运用文献[21]中的犹豫模糊偏好关系集成算子计算得到综合犹豫模糊偏好关系H=(hij)4×4如下:

然后,根据文献[21]中的算法1计算得到每个区块链对应的综合犹豫模糊偏好信息值(由于篇幅的限制,本文仅列出区块链y1对应的综合犹豫模糊偏好信息值h1):
h1={0.551 8,0.291 5,0.302 5,0.498 7,0.335 7,0.346 9,
0.542 7,0.415 8,0.415 8,0.411 0,0.514 9,0.500 3,
0.433 1,0.397 5,0.312 4,0.344 9,0.410 2,0.477 3,
0.465 9,0.311 8,0.564 1,0.571 1,0.622 8,0.634 7}
通过计算综合犹豫模糊偏好信息值hi(i=1,2, 3,4)的得分函数可判别出它们的大小顺序为:h4>h3>h2>h1,那么四个区块链的排序为:y4≻y3≻y2≻y1。所以综合性能最优的区块链为y4。
根据决策结果可知,运用两种方法得到的综合性能最优的区块链是一致的,这说明本文方法是合理有效的。然而,通过上述两种方法得到的区块链优劣排序存在一定的差异。本文方法首先检验并改进概率不完备犹豫模糊偏好关系的一致性,直到所有的概率不完备犹豫模糊偏好关系满足期望一致性后再进行群决策。然而文献[21]中的算法1在没有对犹豫模糊偏好关系进行一致性检验的基础上,直接运用信息集成算子进行决策,这将导致出现不合理的决策结果。事实上,根据原始的概率不完备犹豫模糊偏好关系中的决策信息,可以知道区块链y1对应的偏好信息基本上大于区块链y2,即y1≻y2,这与本文方法得到的决策结果相一致。同时,本文提出的群决策模型考虑到了属性信息值发生的概率,因此,本文的决策模型更为科学可靠,能够提高群决策的正确率。
5 结语
为了研究犹豫模糊元中元素发生的概率信息部分已知或完全未知的决策问题,本文首先引入了概率不完备犹豫模糊偏好关系、概率不完备犹豫模糊偏好关系的期望一致性以及概率不完备犹豫模糊偏好关系的满意加性期望一致性等概念,然后构建一个基于偏差最小化为目标函数的线性最优化模型用于确定概率不完备犹豫模糊偏好关系中元素发生的概率。同时,提出了一个加权概率不完备犹豫模糊偏好关系算子用以将一系列PIHFPR集结成为综合的PIHFPR。最后,建立了一个群体一致性改进模型对多个PIHFPR进行决策分析,最终得到合理可靠的决策结果,并将建立的群决策模型应用于区块链的选择实验中。在本文研究基础上,可以考虑研究概率不完备犹豫模糊语言偏好关系的信息集成方法和基于一致性调整算法、相容性算法的群决策模型,同时将构建的模型方法应用于供应链管理、计算机网络系统、网络安全产品选择等领域,可以进行深入研究。

