改进非线性干扰观测器的机械臂自适应反演滑模控制
邹思凡,吴国庆,2,茅靖峰,朱维南,王玉荣,王 健
(1.南通大学 电气工程学院,江苏 南通 226019; 2.江苏省风能应用技术工程中心,江苏 南通 226019;3.南通理工学院 机械工程学院,江苏 南通 226019)(*通信作者电子邮箱wgq@ntu.edu.cn)
0 引言
机械臂是由关节连接起来的一系列连杆构成的,具有多个自由度,用以抓取和移动物件的装置[1]。作为一个复杂的多输入多输出系统,机械臂系统具有强耦合、未建模动态、时变不确定性、高度非线性等特征。机械臂在生活医疗、农业生产、工业需要甚至是航天航空领域有着广泛的应用前景,因此对机械臂的精确控制得到了高度的重视。机械臂的控制主要是对它的各关节或末端执行器的位置进行控制,使其能够以期望的动态品质跟踪给定的轨迹,即所设计的控制系统的任务是轨迹跟踪控制[2-3]。然而机械臂控制系统具有一定的复杂性,容易受到摩擦力和负载等的干扰,所以传统的PID(Proportion Integration Differentiation)控制方法难以满足准确快速稳定的控制要求。
相比之下,滑模控制(Slide Mode Control,SMC)其实是一种特殊的非线性控制,其表现为控制的间断性。滑模控制可以使系统随着当前的状态有目的地改变,从而使得系统能够根据预定的轨迹实现期望的轨迹运动。因此在机械臂轨迹控制系统中,应用滑模控制律是十分行之有效的。但是传统滑模控制律存在一定的缺陷性,即在开关来回切换时存在惯性,使得运动轨迹穿梭于滑模面两侧,无法严格地从滑面滑向平衡点,从而引起系统抖振,控制精度较低[4-5]。
国内外近年来,基于干扰观测器的控制(Disturbance Observer Based Control,DOBC)与不同控制策略相集成的复合抗干扰策略相继成为热点,Guo等[6]对此进行了详细介绍,尤其针对多源干扰系统提出一系列复合分层抗干扰控制(Composite Hierarchical Anti-disturbance Control,CHADC)策略,促使一类带有多源干扰系统的精细抗干扰问题得到很好的处理。文献[7]中给出了一类具有不确定非线性项和未知外源干扰的多输入多输出系统,应用DOBC 和终端滑模控制(Terminal Sliding Mode,TSM)相结合的控制策略,实现抗干扰的目的。文献[8]中针对带有外源干扰的严格反馈系统,将DOBC与反演(Backstepping)控制相结合,最后实现了闭环系统为半全局一致最终有界的目标。
本文设计了一种改进非线性干扰观测器的自适应反演滑模控制方法:首先设计干扰观测器进行在线测试,在滑模控制律中加入干扰估计值对干扰进行补偿;然后选择合适的设计参数,使观测误差指数型收敛;再引入反演自适应控制律,进一步改善控制系统的跟踪性能;提高了机械臂系统的响应速度并改善了控制精度[10]。
1 空间二自由度机械臂数学建模
根据拉格朗日方法,建立空间二自由度机械臂的动力学方程:

(1)

式(1)描述的机械臂系统的动力学特性[10]如下:

特性2 惯性矩阵J(θ)是对称、有界正定矩阵。

(2)

2 控制器设计


图1 系统控制结构Fig.1 System control structure
2.1 改进的非线性干扰观测器设计
干扰观测器的基本思想是将干扰项及模型参数变化造成的实际系统与重构模型之差作为控制输入端,并将估计出的干扰值作为补偿信号反馈以达到抑制干扰的作用,消除干扰项对系统的影响,使系统对干扰表现出强鲁棒性的作用。
改进前非线性干扰观测器设计为:

(3)

(4)
并且还需要满足:
(5)
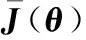
为了克服观测器的不足,本文根据机械臂的数学模型,采用如下形式的非线性观测器[12]:
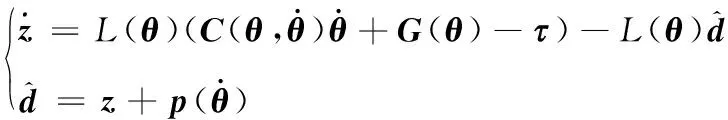
(6)

L(θ)=X-1J-1(θ)
(7)
(8)


(9)
通常情况下,没有干扰d的微分先验知识,假设相对于观测器的动态特性,干扰的变化是缓慢的,即

(10)
定义李雅普诺夫(Lyapunov)函数为:

(11)
其中:J(θ)=J(θ)T>0。于是
(12)
根据观测器式(4),推导可得:

(13)
因而可得观测误差方程为:

(14)
从而得到:
(15)
(16)
于是
(17)
构造不等式
(18)
其中:Γ>0为对称正定阵。则存在Γ′,有
(19)
其中:Γ′>0。
可见,选取合适的Γ,可以使观测器的误差指数趋于零。
非线性干扰观测器的输出送给增益调整模块,由式(1)可知增益调整矩阵为单位阵,则

(20)
通过对线性矩阵不等式(Linear Matrix Inequality,LMI)的求解,可以求得Y的值,进而得到所需的X值。由不等式(18)可见,式中含有非线性项,必须转化为线性矩阵不等式才能求解。令Y=X-1,将YT=(X-1)T和Y=X-1分别乘以式(11)的左右两边,得
(21)
即

YT+Y-YTΓY≥ζI
(22)
即
YT+Y-ζI-YTΓY≥0
根据Schur补定理:假设C为正定矩阵,则A-BC-1BT≥0等价为:
则式(22)等价为:
(23)
2.2 反演滑模控制器设计
滑模变结构控制系统是指存在一个(或几个)切换函数,当系统的状态达到切换函数值时,系统从一个结构转换成另一个结构的系统,也就是在控制过程中,系统结构(或称为模型)可发生变化的系统。如图2 所示。该方法的缺点在于当状态轨迹到达滑模面后,难于严格地沿着滑模面向着平衡点滑动,而是在滑模面两侧来回穿越,从而产生颤动,即抖振问题。

图2 实际滑动模态Fig. 2 Actual sliding mode
现设计滑模控制器,采用反演(Backstepping)方案并选用式(35)的滑模切换函数。采用干扰观测器后,式(1)所述机械臂系统可以写成:
(24)
结合式(24)可知,采用干扰观测器后,本文采用的二自由度机械臂系统中,干扰d变成了D,总干扰减小,因此原机械臂系统可以改写成:
(25)
设θd为机械臂给定指令输入,θ为实际输出。现采用Backstepping方案[14]滑模控制器,使输出θ跟踪指令输入θd。具体步骤包括两个步骤。
1)定义跟踪误差:
z1=θ-θd
(26)
则求导可得:
(27)
定义虚拟控制量:
α1=c1z1
(28)
其中:c1∈Rn×n为对称正定常值矩阵。
(29)
求导得:
(30)
由式(24)和式(29)可得:
(31)
定义反演控制算法下的Lyapunov函数V1:
(32)
则求导可得:
(33)

2)定义反演滑模控制算法下的Lyapunov函数V2:
(34)
定义滑模切换函数:
s=k1z1+z2
(35)
其中:k1∈Rn×n位对称正定常值矩阵。
对式(35)求导可得:
(36)
对式(34)求导可得:

z1Tz2-z1Tc1z1+sT[k1(z2-c1z1) +
(37)
2.3 自适应律设计
在实际应用中,机械臂系统的外部扰动信号D包括很多复杂的因素,通常情况下难以预知D的上界值,因此,在设计控制器时,要注意避开D的上界值。本文在前面反演滑模控制器设计的基础上,引入自适应算法,将外部扰动信号D中无法观测的部分预估出来。
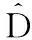
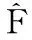
(38)
定义自适应反演滑模控制算法下的Lyapunov函数V3:
(39)
其中:γ为正常数。对式(39)求导得:

z1Tz2-z1Tc1z1+sT[k1(z2-c1z1)+
(40)
根据式(40),设计机械臂的控制律:
τBS=τeq+τvss
(41)
(42)
τvss=-βJhsgn(s)
(43)
其中:τeq位等效控制;τvss为切换控制;h∈Rn×n为对称正定常值矩阵;β为正常数;sgn(s)为切换函数。
自适应律取:
(44)
2.4 稳定性分析
定义改进非线性干扰观测的自适应反演滑模控制算法下的Lyapunov函数V4:
(45)
求导可得:
(46)
将式(14)、式(39)~(43)代入式(45)得:

(47)
参考文献[14]的方法,取:
(48)
适当取值,使P为正定阵,并令z=[z1z2]T,则有
zTPz=z1Tc1z1-z1Tz2+sThs
(49)
则式(46)以改写成:
(50)
式(50)保证跟踪误差在有限时间内收敛为零,使得系统满足Lyapunov稳定性理论条件,z1和z2以指数形式渐近稳定,从而保证系统具有全局意义下指数的渐近稳定性,从而实现了空间二自由度机械臂的轨迹跟踪控制。
3 仿真模型及实例
以二自由度机械臂为例,将式(1)中机械臂动力学模型的各参数表示为:


为了对比控制性能,对滑模控制方法进行仿真,控制器设计为:
图3~4分别为传统滑模控制算法和本文所用控制算法应用在二自由度机械臂轨迹跟踪时的仿真曲线。根据图3~4仿真实验,记录实验数据并作数据分析,可以得到表1对实验数据进行定量分析。

图3 传统滑模控制律仿真曲线Fig. 3 Simulation curve of traditional sliding mode control law
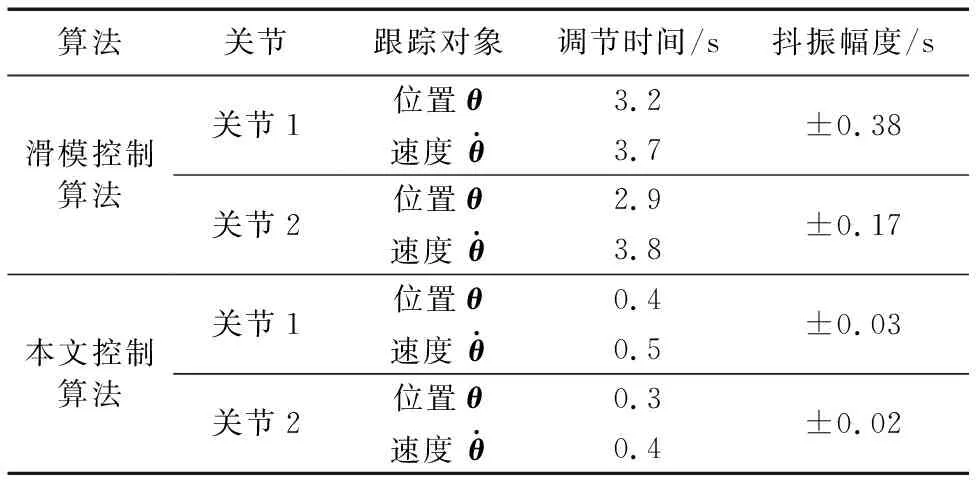
表1 算法改进前后实验数据对比Tab. 1 Comparison of experimental data before and after algorithm improvement
表1为传统滑模算法与本文所用控制算法应用在机械臂仿真实验的数据对比。由表1可知,滑模控制算法下,机械臂的关节1、2位置调节时间分别为3.2 s、2.9 s,而本文所用控制算法下,机械臂的关节1、2位置调节时间分别为0.4 s、0.3 s;同理,改进前后,关节1、2速度跟踪的调节时间分别为3.7 s、3.8 s,0.5 s、0.4 s。因此,这两种方法虽然都可以实现跟踪控制,但是传统的滑模控制方法无法在短时间内快速逼近系统不确定项,而本文所用控制算法解决了这一问题,大幅提高了机械臂轨迹跟踪时的响应速度。

图4 本文控制律仿真曲线Fig. 4 Simulation curve of proposed control law
此外,传统滑模控制算法的不足在于当状态轨迹到达滑模面后,由于式(43)切换函数等控制项的不连续性,使得系统难以严格地沿着滑模面向着平衡点滑动,而是在滑模面两侧来回穿越,从而产生颤动,即抖振问题。因此控制输入曲线中含有大量高频信号,控制输入出现严重的抖振,关节1、2的控制输入在抖振幅值分别在±0.38、±0.17的范围内高频振荡。在实际系统尤其是机电系统中,抖振的存在可能会降低系统的精度、增加系统的能耗,甚至损坏系统的结构,而本文所用的控制算法下,关节1、2的控制输入抖振幅值分别为±0.03、±0.02,所以此时控制输入作用连续、平滑。
因此,本文所用的控制方法既可以较快地跟踪期望轨迹,又可以较好地处理系统惯性参数不确定与外部扰动对空间机械臂系统的影响。
4 结语
本文将滑模反演自适应控制方法与非线性干扰观测器结合起来,提出了一种新型的改进非线性干扰观测器的机械臂自适应反演滑模控制方法。针对传统的滑模控制算法和干扰观测器,本文进行了改进,有效削弱了控制输入的抖振,避免了测量加速度项,并且使动力学方程中的正定惯性矩阵不再受到形式限制,扩大了观测器在其他类模型的应用。通过Matlab/Simulink仿真验证了该方法是行之有效的。实验结果表明,本文所提出的控制方法比传统滑模控制方法具有更好的动态特性,既提高了系统的响应速度,又极大地削弱了系统的抖振,具有良好的控制性能。

