变精度下不完备混合数据的增量式属性约简方法
王映龙,曾 淇,钱文彬,2,舒文豪,黄锦涛
(1.江西农业大学 计算机与信息工程学院, 南昌 330045; 2.江西农业大学 软件学院, 南昌 330045;3.华东交通大学 信息工程学院,南昌 330013)(*通信作者电子邮箱qianwenbin1027@126.com)
0 引言
在大数据时代,信息系统中的数据随着时间的变化而不断更新。如何快速针对大量的动态数据中更新属性约简结果,已成为粒计算和知识发现领域的研究热点[1-5]。针对动态数据,不同的信息系统处理数据的方法是不一样的,一些研究者对处理动态更新的数据集进行了相关探索,并已取得许多有意义的成果[6-9]。针对信息系统中数据的动态更新,采用增量式计算属性约简方法成为一种可行的解决途径。对于完备的信息系统,文献[3]中利用差别矩阵方法对属性约简进行了增量式更新;文献[6]中以信息粒度作为启发信息设计了增量式计算属性约简方法;文献[7]中为应对动态变化的海量数据,设计了两种并行增量更新粗糙近似集的算法;文献[8]中提出了基于二进制差别矩阵和信息熵的动态约简算法,有效缩小了算法的搜索空间;文献[9]中结合变精度粗糙集模型,构造出近似集增量式更新的矩阵算法。
在信息系统中,数据的激增难免会导致数据的丢失,对于信息系统中存在缺失值的问题,一般采用以下两种方法:一是对缺失值进行删除、替换等处理,使不完备数据变成完备数据后再进行属性约简;二是不对缺失值进行预处理,直接采用能够处理不完备数据集的计算模型进行属性约简。当前第二种方法运用较广泛,如文献[10]中在融入一定程度误差的分类思想下,对不完备信息系统提出基于限制容差关系的程度多粒度粗糙集, 结合容差粗糙集模型,提出二进制区分矩阵的增量式属性约简方法。文献[11]中介绍了三个矩阵在四种不同扩展关系下的增量式更新方法。文献[12]中设计了一种基于正向近似的通用特征选择加速算法处理海量数据。除了经典粗糙集探讨的名义型变量,数值型变量广泛存在于应用领域,为解决大量数值型数据的更新问题,文献[13]中针对连续型属性的数据集,研究了基于邻域粗糙集的特征子集增量式更新方法,通过分析新增对象对正域的影响,选择性地动态更新,避免了重复操作。文献[14]中从信息观出发,运用条件熵的度量方法,设计了完备邻域系统中增量式属性约简算法。
上述研究针对不同的数据类型,分别在完备或不完备信息系统中设计了增量式更新方法,由于现实生活中同时存在大量的不完备、连续数值型、名义型数据的情况,现有的邻域粗糙集增量式更新计算方法对上述情况讨论较少。为此,本文针对决策信息系统中同时存在大量的不完备型、连续数值型、名义型混合数据的情况,研究如何有效处理动态的数据,实现属性约简的增量式更新。首先,分析了对象增量式更新所引起的条件熵变化情况和更新机制;然后,结合可变精度的粗糙集概念,构造了面向不完备邻域决策系统的对象增量式更新属性约简算法,该算法能直接处理不完备的数值型和符号型混合数据,最后,通过实例分析和实验比较验证了算法的有效性。
1 基础理论
若给定一个决策信息系统DS=(U,C,D,V),其中U={x1,x2,…,xn}表示非空有限对象集合,称为论域;C是条件属性集合,D是决策属性,C∩D=∅,若D=∅,则决策系统转换为信息系统;V为属性值域,对于∀a∈C∪D,Va为属性a的值域,xi(a)为对象xi在属性a上的取值。
如果V中包含连续型和符号型等属性类型的对象,则该系统称为邻域决策系统。在邻域决策系统中,当部分对象的属性值缺失时,则该系统称为不完备邻域决策系统,缺失值用“*”表示。
定义1[1]设DS=(U,C,D,V)是不完备邻域决策系统,对于∀x∈U,定义x在A=C∪D上的邻域信息粒子为NA(x)={y|y∈U,ΔA(x,y)≤δ,δ≥0},其中δ表示邻域半径,ΔA:U×U→R为U上的一个度量,满足以下性质:
1)∀x,y∈U, ΔA(x,y)≥0, 当ΔA(x,y)=0时, ∀ai∈A,ai(x)=ai(y);
2)∀x,y∈U,ΔA(x,y)=ΔA(y,x);
3)∀x,y,z∈U,ΔA(x,z)≤ΔA(x,y)+ΔA(y,z)。
对于连续型的数据,采用欧氏距离度量:
对于符号型的数据中,可定义:
当δ=0时,变为经典粗糙集模型。
定义2[15]将邻域等价关系扩展到符号型、连续型和缺失型等未知属性共存下的不完备模糊系统,可得到以下广义邻域关系:
R(x)={(x,y)∈U2:∀a∈x∩f1(x)=f1(y),
a(x)∈δ(y,a)∪a(y)∈δ(x,a)∪a(x)=
*∪a(y)=*}
广义邻域关系满足自反性,但不一定满足对称性和传递性,因为任意对象与其自身是不可分辨的,所以任何等价关系均满足自反性。在这里放宽了对称性和传递性的限制,扩展了应用范围。
信息熵作为一种度量信息的不确定性的有效方法,实现对信息的量化度量。梁吉业等在文献[16]给出了信息系统在经典粗糙集计算模型下信息熵的统一表示:
定义3[16]设S=(U,B)是一个决策信息系统,粒度K(B)=(SB(x1),SB(x2),…,SB(x|U|)),其中SB(xi)是对象xi在属性B下的类,则B的信息熵为:
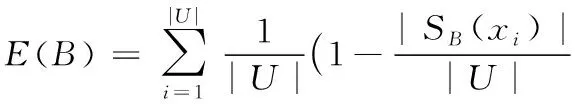
2 可变精度的属性约简计算模型
现有的文献大多是针对完备的单一连续型数据对邻域决策系统展开研究,本文提出的不完备可变精度的粗糙集计算方法,则结合了广义邻域下可变精度的粗糙集模型,能直接处理不完备的数值型和符号型混合数据。
定义4[17]DS=(U,C,D,V)是不完备邻域决策系统,X和Y是U上的两个非空子集,定义集合X关于集合Y的相对错误分类率:
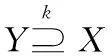
定义5 给定DS=(U,C,D,V)是不完备邻域决策系统,B⊆C,决策属性集合D={d1,d2,…,dn},0≤k<0.5,在可变精度k下,属性集B相对于决策属性D的上、下近似分别为:
决策属性值di在可变精度k的上近似是:U中不小于k的分类对象划分到di上邻域信息粒子的集合,下近似是:U中不小于1-k的分类对象划分到di上邻域信息粒子的集合。根据多粒度粗糙集的思想,在可变精度不完备邻域决策系统中,通过对邻域粒度δ和可变精度k的控制来区分不同的信息。邻域粒度δ越小,可变精度k取值越优,区分能力越强。
定义6 给定DS=(U,C,D,V)是不完备邻域决策系统,对象x、y∈U,ΔA(x,y)为对象x、y在U上的一定度量,对象x、y在条件属性C上的区分值ΔC(x,y)为:
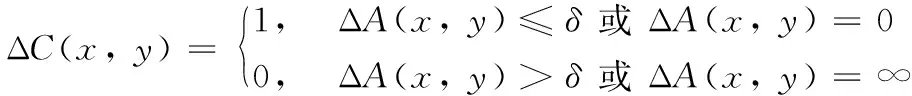
分两种情况:1)当对象x、y的度量值ΔA(x,y)=0,或者小于等于邻域半径,则对象x、y在条件属性C上的区分值ΔC(x,y)=1。 2)当对象x、y的度量值为无穷大,或者大于邻域半径,则对象x、y在条件属性C上的区分值ΔC(x,y)=0。
定义7 给定DS=(U,C,D,V)是不完备邻域决策系统,对象x,y∈U,C是条件属性集合,ΔA(x,y)为对象x、y在U上的一定度量,ΔC(x,y)为对象x、y在条件属性C上的区分值,可变精度k为:
性质1 在不完备邻域决策系统DS=(U,C,D,V)中,对象xi,xj∈U,xi(D)为对象xi在决策属性D上的取值,xi(C0)为对象xi在符号型条件属性C0上的取值,δxi(C1)为对象xi在连续型属性C1上的邻域。f:U×C∪D→V是一个信息函数,它对一个对象的每一个属性赋予一个信息值,即∀a∈C∪D,x∈U,有f(x,a)∈Va。对含有缺失条件属性值的对象判定:当xi(D)=xj(D)时,根据定义7判定,如果xi(C0)=xj(C0),δxi(C)=δxj(C),则f(xi,a)=f(xj,a);否则f(xi,a)≠f(xj,a)。
实例分析 在不完备邻域决策系统DS=(U,C,D,V)中,条件属性集合为C={C1,C2,C3,C4},决策属性集为D={d1,d2},{C1,C2,C3}为连续型数值属性,{C4}为符号型属性,下面通过表1的实例说明。
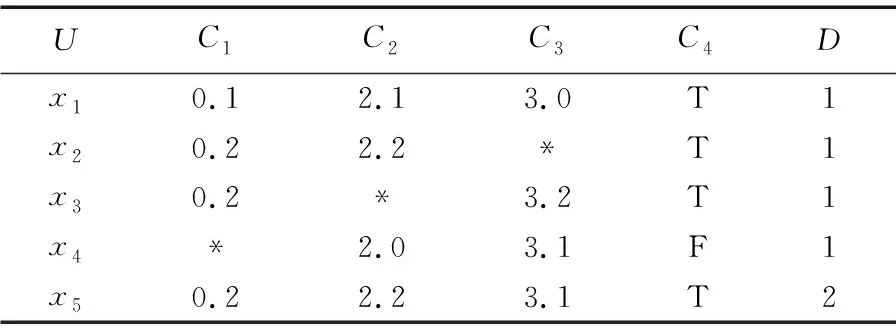
表1 不完备邻域决策系统Tab. 1 Incomplete neighborhood decision system
令δ=0.1,k=0.2,因为对象x1、x5的决策属性D取值不同,连续型的属性值都在邻域范围内,名义型属性取值相同,也不能视为同一类;因为k=0.2,两个对象在C1、C2、C3、C4属性中只能有一个属性取值不同或不在同一邻域,所以x1、x2属于同一类,x1与x3、x4不属于同一类。
针对存在不完备的数值型和符号型混合数据的系统,本文结合可变精度的粗糙集模型,下面给出了基于条件熵的属性约简方法。
对于经典粗糙集模型,定义3给出了在信息系统中信息熵的统一表示。本文在此基础上对于邻域粗糙集模型,给出了可变精度k下信息熵的定义与公式。
定义8 给定DS=(U,C,D,V)是不完备邻域决策系统,对象xi在条件属性C下的邻域为δC(xi),k为可变精度,则在不完备邻域决策系统中条件属性C的信息熵为:
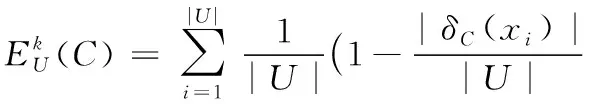
通过定义8的公式可以推出定理1决策属性D关于条件属性C的条件熵的计算公式。
定理1 给定DS=(U,C,D,V)是不完备邻域决策系统,对象xi在条件属性C下的邻域为δC(xi),在决策属性D下的邻域为δD(xi),则在不完备邻域决策系统中决策属性D关于条件属性C的条件熵为:
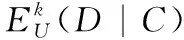
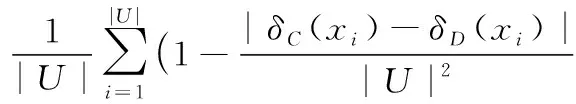
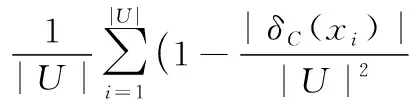

定义10 给定DS=(U,C,D,V)是不完备邻域决策系统,B⊆C,对于∀a∈C-B,则属性a相对于属性集B的重要性计算方式为:
3 属性约简的增量式更新机制
对象增加时,为有效利用原属性约简集结果,避免算法的重复计算,本章首先分析了在不完备邻域决策系统中,新增对象v后条件熵的变化情况;然后结合可变精度粗糙集模型的概念,给出了针对不同情况下条件熵的计算公式。
新增对象v在属性集B⊆C上的邻域δB(v)及其决策类δD(v),其条件熵的变化有4种情况,如图1所示。

图1 条件熵的增量式更新机制Fig. 1 Incremental update mechanism of conditional entropy
1)新增对象v在属性集B上的邻域只有其自身无其他对象,且新增对象v的决策类是系统中没有的;
2)新增对象v在属性集B上的邻域只有其自身无其他对象,且新增对象v的决策类是系统中已有的;
3)新增对象v在属性集B上的邻域还有其他对象,且新增对象v的决策类是系统中没有的;
4)新增对象v在属性集B上的邻域还有其他对象,且新增对象v的决策类是系统中已有的。
对于上述1)~2)两种情况,可以利用定理2中的公式得到新的条件熵。
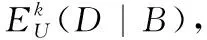


对于上述3)和4)两种情况,可以利用定理3中的公式得到新的条件熵。
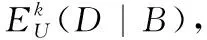
2|δB(v)-δD(v)|)

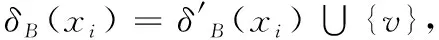
综上所述,对于在系统中新增对象v后出现的4种情况均满足:
2|δB(x)-δD(x)|)
所以由此可得出定理4,该定理满足不完备邻域决策系统中对象增量式更新的情况。
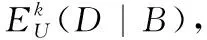
2|δB(v)-δD(v)|)
证明 根据定理2和定理3,显然同理可证得。
4 增量式属性约简方法
4.1 不完备邻域数据的增量式属性约简
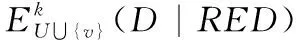
根据以上分析,算法的具体描述如下。
输入 不完备邻域决策系统DS=(U,C,D,V)的约简集RED及其条件熵,邻域半径δ,可变精度k,新增对象v。
输出 属性约简结果RED′。
步骤1 初始化RED′=∅。
步骤2 分别计算约简集RED下对象v的邻域δRED(v)和对象v的决策类邻域δD(v),如果δRED(v)-δD(v)≠∅,跳转至步骤3;否则跳转至步骤6。

步骤4 计算新增对象v和δRED(v)-δD(v)所得对象在条件属性集{C-RED}下的属性约简为RED1,令RED′=RED∪RED1。
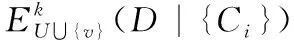
4.2 算法复杂度分析和比较
算法表述中|U|代表系统中对象的个数,|C|代表条件属性的个数,|RED|代表原约简属性个数。对于上述增量式属性约简算法的时间复杂度分析如下:
步骤1 初始化RED′=∅的时间复杂度为O(1)。
步骤2 计算约简集RED下对象v的邻域δRED(v)的时间复杂度为O(|U||RED|),计算对象v的决策类邻域δD(v)的时间复杂度为O(|U|),所以步骤2的时间复杂度为O(|U||RED|)。
步骤3 计算条件属性集C下对象v的邻域δC(v)的时间复杂度为O(|U||C|),所以步骤3的时间复杂度为O(|U||C|)。
步骤4 计算新增对象v和δRED(v)-δD(v)所得对象在条件属性集{C-RED}下的属性约简为RED1,设δRED(v)-δD(v)所得对象为m个,则m个对象计算δRED(xi)-δD(xi)的时间复杂度为O(m(|C-RED|)),最坏情况下所得属性约简RED1=C-RED,计算约简集RED1的时间复杂度为O(m(|C-RED|2)),最坏情况下当m=|U|时,该步的时间复杂度为O((|U|+1)(|C-RED|2),所以步骤4最坏的时间复杂度为O((|U|+1)(|C-RED|2)。

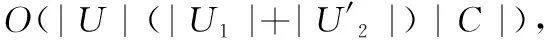
4.3 与基于正域约简算法及启发式约简算法比较
与基于正域约简算法及基于启发式约简算法相比,本文提出的变精度不完备邻域系统的增量式属性约简算法具有以下优点:
1)基于的正域属性约简算法及基于启发式属性约简算法大多针对静态的信息数据,如果用算法简单重复进行属性约简,那势必会导致时间消耗过高和大量占用系统空间资源,并造成无法实时更新系统数据的问题。本文提出的增量式属性约简算法可直接用于新增对象的属性约简,并能反向剔除冗余数据,有效减少了系统资源的消耗量。
2)基于正域属性约简算法及基于启发式属性约简算法多数适用于离散型属性约简,且较难直接处理含有不完备型混合数据。而变精度不完备邻域系统的增量式属性约简算法可直接处理含有不完备的离散型和连续型混合数据,并能通过调节可变精度,得到数据不同层次的信息粒度。
3)变精度不完备邻域系统的增量式属性约简算法是对基于条件熵启发式约简算法的进一步扩展,本文的属性约简算法改进了经典的条件熵公式,先对新增对象的邻域进行计算和分析,根据具体的情况再选择性地进行公式计算,有效减少了计算量。
5 实例分析
以表2中的不完备邻域决策系统为例,分析本文算法的有效性。设条件属性集为{C1,C2,C3,C4}, 决策属性为{D}。设置邻域半径δ=0.35,即两对象之间的邻域半径小于等于0.35;可变精度k=0.2,即两个对象在条件属性集中只能有一个属性取值不同或不在同一邻域中;已知该邻域决策系统的一个约简集RED={C3,C4}。

表2 不完备邻域决策系统Tab. 2 Incomplete neighborhood decision system
1)如果新增对象v={0.93,*,0.90,T,4},根据算法步骤2计算得δRED(v)-δD(v)=∅,则跳转至算法步骤6,输出RED={C3,C4},算法结束。这属于第一种情况:δRED(v)={v},δD(v)={v},原属性约简集RED可以区分新增对象v,属性约简结果保持不变。
2)如果新增对象v={0.95,0.02,0.89,*,3},根据算法步骤2计算得δRED(v)-δD(v)=∅,则跳转至算法步骤6,输出RED={C3,C4},算法结束。这属于第二种情况:δRED(v)={v},δD(v)={x4,x6,v},原属性约简集RED可以区分新增对象v,属性约简结果保持不变。
3)如果新增对象v={0.35,0.67,0.79,T,4},根据算法步骤2计算可得δRED(v)-δD(v)={x5},跳转至步骤3计算δC(v)={x5,v},因为δC(v)=δRED(v),则跳转至算法步骤6,输出RED={C3,C4},算法结束。这属于第三种情况:δB(v)={x5,v},δD(v)={v},因为新增对象v在条件属性集C下的邻域δC(v)等于在原属性约简集RED下的邻域δRED(v),所以原属性约简集RED可以区分新增对象v,属性约简结果保持不变。

然后根据算法步骤4,计算新增对象v和δRED(v)-δD(v)所得对象{x1,x4,x5}在条件属性集{C-RED}下的属性约简结果为RED1={C1}和RED1={C2},令RED′=RED∪RED1,得到新的约简集{C1,C3,C4}和{C2,C3,C4}。
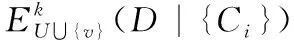

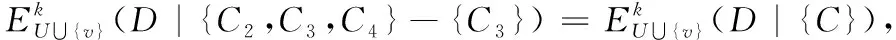
算法转至步骤6,输出属性约简结果。因此,按照以上算法步骤, 当δ=0.35,可变精度k=0.2时,不完备邻域决策系统的新增对象后的属性约简为{C2,C4}。这属于第三种情况:δB(v)={x5,v},δD(v)={v},因为新增对象v在条件属性集C下的邻域δC(v)不等于在原属性约简集RED下的邻域δRED(v),原属性约简集RED不可以区分新增对象v,则需根据算法重新计算属性约简。
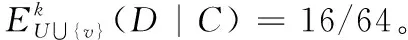
然后根据算法步骤4,计算新增的对象v和δRED(v)-δD(v)所得对象{x7}在条件属性集{C-RED}下的属性约简结果为RED1={C1},令RED′=RED∪RED1,得到新的约简集{C1,C3,C4};
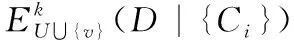
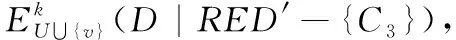
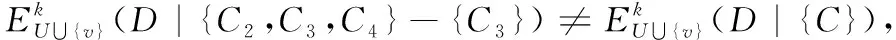
算法转至步骤6,输出属性约简结果。因此,按照以上算法步骤, 当δ=0.35,可变精度k=0.2时,不完备邻域决策系统的新增对象后的属性约简为{C1,C3,C4}。此情况属于属性约简更新的第四种情况,则有δB(v)={x3,x6,x7,v},δD(v)={x4,x6,v},原属性约简集RED不可以区分新增对象v,则需根据算法重新计算属性约简。
通过上述实例分析,本文算法的最坏时间复杂度为O((|U|+1)(|C-RED|2)。若采用静态的基于条件熵的属性约简算法分析不完备邻域决策系统,则算法在增加对象后的时间复杂度为O(|U+1|2|C|3),可见增量式方法能够有效地降低算法的时间复杂度。在存储空间上,计算表2不完备邻域决策系统中数据,本文算法需42个存储空间,若采用差别矩阵方法则需196个空间用于存储邻域矩阵元素,本文算法占用的空间相对较少。因此,本文算法在计算效率和存储空间上较好,且能处理完备的数值型和符号型混合数据,具有较好的扩展性。
6 实验分析和比较
为了进一步验证本文算法的有效性,从UCI数据集中选取了Echocardiogram、Hepatitis、Automobile、Credit、Dermatology五个含有连续型数据和名义型数据的混合型不完备数据集进行实验测试和分析。五个真实数据集的相关信息描述如表3所示。实验的测试环境为:CPU Intel Core i5-4590s (3.0 GHz),内存8.0 GB,操作系统为Windows 10,算法编程语言是Python 3.5, 采用的集成开发环境为Anaconda 2.6, 采用的开发工具为PyCharm。

表3 UCI数据集描述Tab. 3 Description of UCI data sets
在实验测试的过程中,将五组数据集中的每组数据集分为训练数据集和测试数据集两部分。为验证本文算法的有效性和可行性,对每个数据集进行四次实验测试和比较。在第一次实验过程中,取数据集的前60%部分作为训练数据集,其后10%的部分作为测试数据集;后面三次实验的训练数据集的规模以10%为幅度增长。同时,为了进一步验证本文算法,将提出的增量式属性约简算法和静态约简算法进行实验分析和对比。在实验过程中,若可变精度k=0.2和邻域半径δ=0.2时,对属性约简结果和算法的运行时间进行实验分析和对比。
由表4可知,本文提出的增量式属性约简和静态的属性约简方法相比,当数据集的数据量相同时,五个数据集的属性约简结果相同。但当数据量不同时,每个数据集得到的属性约简的结果可能存在差异,如对于Echocardiogram和Hepatitis数据集来说,在四种不同规模的数据量下,虽然约简后的属性个数相同,但约简后的属性子集不完全一致。在Autos数据集下,在四种不同规模的数据集下,约简后的属性个数和约简后的属性子集相同。对于Credit和Dermatology数据集来说,当数据量为70%和80%时,约简后的属性个数和约简后的属性子集相同。同时,当数据量相同时,属性约简的效果与数据集相关,例如,当数据量为100%时,Echocardiogram、Hepatitis、Autos、Credit和Dermatology数据集原属性个数分别由12、19、25、17和34个约简至6、7、10、11和13个,分别占原属性个数的50.0%、36.8%、40.0%、64.7%和38.2%。由此可知,本文的约简算法能有效剔除数据中的冗余属性。

表4 增量式与静态属性约简算法在不同数据集上的实验结果对比Tab. 4 Comparison of experimental results of incremental and static attribute reduction algorithms on different data sets
由实验结果可知,从算法的执行时间上来看,由于本文算法每次仅需处理新增的10%数据量,而静态的约简算法需对新增数据量的数据集进行重新计算,如Echocardiogram数据集,在不同数据量下,本文算法执行时间变化不大,平均耗时为2.98 s,而静态的约简算法执行时间随数据量的增多而明显增长,平均耗时为284.91 s。通过UCI数据集中五个真实的混合型数据集的实验比较和分析,增量式算法在五个数据集的平均耗时分别为2.99 s、3.13 s、9.70 s、274.19 s和50.87 s,静态算法的平均耗时分别为284.92 s、302.76 s、1 062.23 s、3 510.79 s和667.85 s,由此可知,在执行时间方面,增量式属性约简算法要显著好于静态的约简算法。同时通过实验发现,算法的执行时间与数据集的实例个数、属性个数和属性值类型的分布直接相关。如Echocardiogram、Hepatitis数据集的实例个数较少,属性约简消耗的时间也较少;而Credit数据集的实例个数较多,使得属性约简花费的时间也较多。
综上所述,通过表4的实验结果可知,属性约简的结果与数据集的数据量大小相关,属性约简所耗费的计算时间随数据量的增大而增多;同时,属性约简的时间与数据集的特征个数相关。由此可知,本文算法可在保持原属性约简结果相同的前提下,显著地缩短属性约简的计算时间,提高算法的运行效率。本文的研究结果为大规模不完备混合数据的处理和分析提供了一种可借鉴的方法。
7 结语
针对存在混合型数据集的不完备邻域决策系统中对象增量式属性约简问题,本文首先分析了对象增量式更新所引起的条件熵变化情况,然后结合可变精度的粗糙集概念,构造了面向不完备邻域决策系统的对象增量式更新属性约简算法,通过实例分析和实验比较可知,该方法能对不完备的数值型和名义型混合数据进行属性约简,可显著缩短算法的运行时间。由于本文主要是研究对象增加后的属性约简增量更新,下一步将在不完备邻域决策系统中考虑属性增加后属性约简的更新问题。

