探究·变式·拓展·总结
——从一道向量习题的教学处理说起
☉江苏省郑集高级中学 王 鹏
教学过程中,学生需要借助习题的练习来巩固对知识的理解,并由此来发展自己的数学思维和问题解决能力,教师在此过程中也要提供适当的引导和帮助.下面笔者结合一道向量习题的教学处理,谈谈自己的认识.
一、探索一题多解,全方位分析问题
师:在前面的复习过程中,我们回顾了平面向量的概念以及坐标表示方法,特别是关于向量问题的分析过程中,我们一直在强调怎样的数学思想?
生:数形结合.
师:很好,我来看下面这样一个问题.

师:这是一个将向量作为载体的面积问题,它的思路切入点在什么位置呢?大家要积极发掘相关条件之间的关系,并寻求问题的解决方法.
学生进行思考,并积极讨论,将自己对问题的基本看法展示出来.
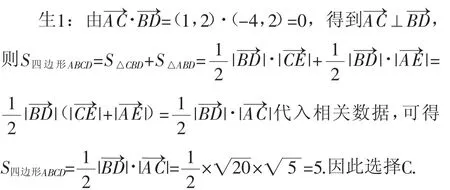
生2:可以从几何的方法来处理,对向量进行平移,画出四边形ABCD(如图1所示),因此有
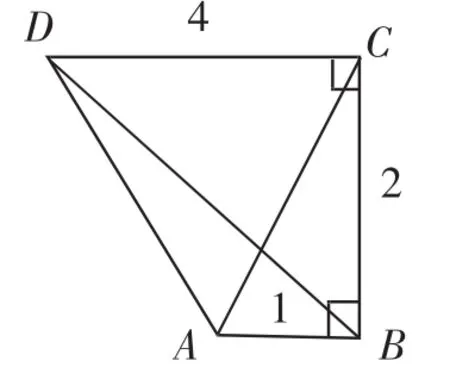
图1
师:通过比较,我们发现这个方法显然没有用到之前的隐含条件,它从数形结合的角度着手,完成了问题的处理.那么这个方法是否存在普遍性呢?现在,我们有这样一个问题:明确告诉你A—→C与B—→D没有垂直关系,如何求解四边形ABCD的面积?
反思:这个问题的解题过程是我们引导学生进行说题的过程,所谓“说题”,这是一个相对新颖的教学名词,在概念上有点类似于“说课”.但是和“说课”却也有所差别,说题的主体可以是老师,比如教师在讨论命题设想,或是讨论试题评讲时,我们经常会通过“说题”的方法探讨相关问题有什么优势或特点,在讲评过程中存在什么注意点等,从这一层面来讲,说题和说课存在相通之处.和说课不同的地方是,说题也可以是一种学生行为,面对一个问题,学生从自己认识的角度着手,对问题情境展开分析,并将自己的思路展示出来,学生的说题过程也是一种交流和讨论的过程,他们在彼此交流中互相启发,并最终形成认识和理解.
在上述问题分析过程中,如果学生将自己的思路定格为第一种处理方法,则很容易让学生形成思维定式,这也导致如果下次学生遇到问题:明确告知A—→C与B—→D没有垂直关系,求解四边形的面积.学生很可能在思维上陷入停滞,而我们在习题教学的过程中引导学生展开分析和讨论,这样的处理可以让学生形成更加深刻的认识.
很多学生在学习过程中经常止步于一个答案,貌似这样处理,问题就已经全部解决.但是,这样可能在一定程度上制约了他们思维的发展,因此一题多解往往都是我们引导学生展开探索的重要手段.一题多解的研究能够推动学生将思路向更深层次发展,这可以让学生的思维更加灵活多变,也有助于学生思维品质的提升.
二、变式处理,活化学生的数学思维
在上述问题的基础上,我们对问题进行变式处理,由此来推动学生,让他们的思维向更加活跃的层面推进和发展.比如在处理上述问题的过程中,我们可以用以下做法来进行变式.
师:现在这个题目中已经不存在原先题目中的垂直条件,因此原本的第一种方法已经无法继续使用,我们该如何处理呢?
生3:可以进行向量的平移,如图2所示,可得S四边形ABCD=S梯形ABED-S△CDE=

图2
生4:还可以这么处理,S四边形ABCD=
师:不错,我们可以类比之前同学的处理方法,对向量进行平移,最终得到四边形的面积.你们还有其他的做法吗?
学生继续讨论,又给出了一些其他的处理方法.
反思:在课堂教学的过程中,我们要力争让学生真正成为学习的主人,我们也要充分尊重学生的个人见解,对他们的创新意识和发散思维进行保护,同时也有效拓展学生的探究空间.我们要让学生能够自我感受到数学探究过程中的那份专注和激情,也让学生能够感受到挑战带来的喜悦和兴奋.
上述案例其实是对原先例题的发展,直接给出一个不垂直的条件,为学生的探究提供了一个新的平台.学生在处理过程中将充分运用向量的夹角公式、三角转化公式等等.如此则能促使学生的认识得到发展和提升.
三、有效拓展,引导学生思维向纵深发展
对于上述问题,教师继续进行拓展:在一个四边形ABCD中,A—→C=(a,b),B—→D=(c,d),则四边形ABCD的面积是多少?
师:结合上述问题,我们是否可以推导出四边形ABCD的面积公式?
生5:我们对图形进行适当转化,如图3所示,S四边形ABCD=S△ABD+S△DBC=
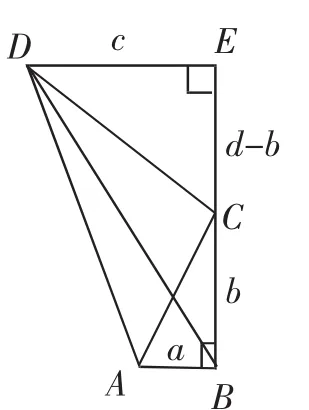
图3
生6:我还有这样一个想法,S四边形ABCD=
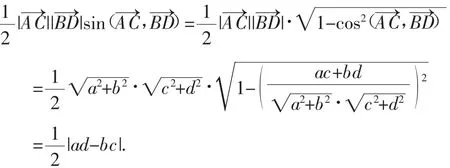
师:很好!这两种方法都能非常好地解决问题,同时还能充分体现出数形结合的基本思想.由此我们通过对最先那个问题的处理,得到了一个一般性的结论:在一个四边形ABCD中
反思:在上述教学过程中,我们在经过一题多解、变式处理之后,果断引导学生进行拓展,让学生在更进一步的思考和讨论中完成结论的总结.这一过程流畅而自然,很容易让学生产生深刻的印象.事实上,如果我们将预设的结论强加在学生的身上,他们将相当勉强,而且很可能第二天就忘掉,所以让学生在自主探索时形成认识和理解,这样才是真正属于学生的认识.
四、总结归纳,促使学生获得更大提升
就学生的数学学习而言,我们不能让他们的研究止步于一个结论的获得,结论探索过程中所产生的思维方法或数学思想,这些都是我们在教学过程中需要重点关注的.比如,在上述问题讨论之后,我们安排学生展开总结归纳,交流经验和体会.
师:通过刚才的研究,你们有什么体会吗?
生7:经过刚才的思考和研究,我感到特别有成就感.
生9:数形结合的思想真是太奇妙了.
师:在上述问题的分析和研究中,我们抓住两个主要角度来进行分析研究,其一是向量的坐标运算,其二是向量的几何意义,最终完成了四边形面积的求解,而且我们还由数量积的计算发展到向量夹角公式的研究,最后通过数形结合思想的运用得到了更加普遍的结论.
反思:在学生完成探索和研究之后,教师要引导学生展开分析,要鼓励学生结合自己学习中的感受来提炼学习经验,这是相当重要的.正所谓“实践出真知”,如果只有实践,而缺乏一个总结和提炼的过程,学生的真知将很难自己浮出水面,所以这一过程需要老师引导学生在总结中概括出来.
综上所述,在有限的数学学习时间中,教师要为学生提供说题、探索、发现、总结的机会,让学生能够在主动研究和分析中获得真知,完成能力的飞跃.
——作业改革探索与实践

