小议公开课教学的几个关注点——以《函数奇偶性》为例

☉江苏省灌云高级中学 朱磊磊

众所周知，数学教师的基本素养之一是良好地演绎公开课.数学公开课是一个数学教师综合素养能力的集中体现，可以这么说，从教学的设计、学案的设计、课堂的演绎、板书的呈现、学生的交流、课堂的控制、课后的反思，无不体现了教师全面的综合素养.笔者以一堂自身设计的《函数奇偶性》为例，跟大家探讨课堂教学的设计与反思，并关注公开课教学的几个关键点.

一、关注情境

情境是中学数学教学的重要手段，之所以在公开课教学中这么重要，笔者以为不外乎两个因素：其一，数学知识是生活的抽象；其二，数学是物理载体的本质.因此以情境为设计的知识点，往往将本课需要表达的数学本质寓于其中，让学生从生活的角度去感受数学知识的存在，这恰恰是体现了数学之用.

《函数奇偶性》情境设计：

师：给出下列图片，请仔细观察，这些图片有什么共性？有什么区别？

生：我发现这些图片都具有对称性，有些是轴对称，有些是中心对称.

师：很好.同学们发现了图片的共性——对称性，也发现了这些图片的区别，是不同的对称性——轴对称和中心对称.请你说一说，这些图片中的对称是如何看待的？

生：蝴蝶是大自然中完美对称的生物，它这样的形态有着一定的生态规律；太极是中国古代道家的著名标志，象征着阴阳两极交替环绕，呈现中心对称之美；第三幅是一张报纸上的截图，我们发现两位美国总统候选人以中心对称的方式排布，给人以极强的视觉冲击效果，可见对称美的作用；最后一幅是印度泰姬陵建筑，完美的轴对称建造，呈现大气磅礴、华丽堂皇，视觉冲击力极强.

师：很好！大家想一想，我们将这些图片的物理属性除去，就可以得到我们数学中的对称之美.

说明：公开课教学的起始步骤极为重要，用华东师大教授张奠宙先生的话说，教材中的数学定义都是线性的、冰冷的，教师如何将线性的知识转化为火热的思考，是我们教学需要关注的.笔者以为，好好地理解老教授的话，不正是需要用感性的知识去引导学生做理性的思考吗？因此情境手段成为我们启发学生思考、加深学生理解知识的重要手段，不可或缺.好的情境往往让课堂成功了一半，因此公开课教学的第一个关键点要让学生获得足够的思考、在视觉层面可以形成一定的冲击，让我们的教学开展得更有意义.

二、关注建构

师：同学们，如何看待一个图形是否不对称呢？

生：这很容易，只要两边不完全一样就可以了.

师：你能否举个例子？

生：比如刚刚的蝴蝶，如果一边的翅膀受伤折断了，那么这只蝴蝶的形态就不是轴对称图形了.

师：那么你把问题抽象一下，能否用一个具体的数学模型举个例子呢？

生：比如函数f（x）=x2（x∈R）是轴对称图形，如图1，但是f（x）=x2（x∈R且x≠1.3）（在点A处没有定义）就不是一个轴对称图形了，如图2.

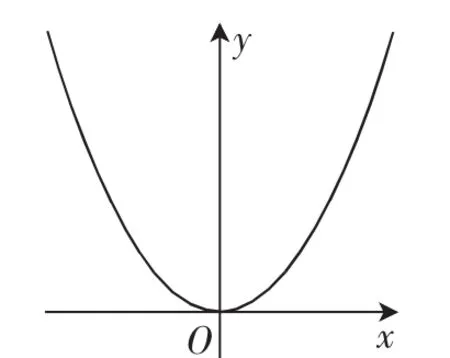
图1

图2

师：理解到位.那么请大家说一说，我们如何给轴对称函数、中心对称函数下一个定义呢？

生：应该是图形的左边和右边完全对称！

师：说得非常正确！但是让我们用数学的语言进行表述，要进一步抽象：对定义域内的任何一个自变量x，都有f（-x）=f（x），那么函数关于y轴对称.请你仿照此轴对称的定义，描述函数关于原点成中心对称的定义.

生：对定义域内的任何一个自变量x，都有f（-x）=-f（x），那么函数关于原点成中心对称.

说明：对于概念的建构是教学的难点，对于轴对称和中心对称的概念建构，如何通过刚刚的情境进一步合理地过渡？一直是教学思考的.我们发现，这里的四幅情境教学的图片，不仅仅给学生感官上的冲击这么简单，更要从图片的认知中获得数学抽象的素养，从而提升数学学习的能力.笔者实施过程中也是反其道而行之，先请学生思考：没有对称性怎么进行说明？学生自然而然想到了使用存在性进行说明，即说明一处不对称就可以.在抽象奇偶函数概念的时候，这里采用类比的教学方式帮助学生建构概念，首先是教师在学生感性的基础上进行了抽象偶函数概念，学生类比建构奇函数概念.笔者以为，这种方式是比较符合教学实际的.那种完全依赖学生抽象数学概念的建构，至少在今天的数学课堂中是不现实的，是伪建构.众所周知，函数的各种概念历经上百年才形成，你不能也不可能要求学生在短短十分钟左右的时间内获得数学本质的抽象，因此公开课教学在建构部分需要做到合适的处理，忌教师直接给出，也忌学生无休止地伪探究.

三、关注思维

数学教学的最终目的是帮助学生建立思维，获得更高的数学素养，以便学生用数学的思维来思考生活.因此公开课教学也需要关注学生思维的发生、发展，在公开课教学中加以渗透和展示.

给出两个问题两组变式，请学生判断、思考、解决：

问题1：判断下列函数的奇偶性：

辨析：给出的这个基本题组，是考查学生对于刚刚建构的概念是否掌握，能否将具体的概念运用到实际问题中去.对于基本初等函数奇偶性的判断，主要是抓住两个关键点，其一是定义域是否关于原点对称；第二是考虑f（-x）=-f（x）还是f（-x）=f（x）？公开课教学也要回归教学的基础，这一点也是近年来公开课教学最大的呼声，切忌将公开课演绎的“空、大、闹”，而要注重数学学科的特性，回归“真、用、静”，因此这些回归数学的真实操作必不可少.

问题2：判断下列函数的奇偶性：

辨析：对思维的提升，更需要一些合理的数学问题作为铺垫，要更进一步理解单调性，我们需要用更为抽象的函数模型给予思维的提炼.因此笔者给出了更为复杂的函数模型，在这些模型中学生又能更深刻地理解概念中“任意自变量”“都有”这些高等数学的严密用语，从而提炼了思维.

解析：（1）（2）略.

（3）f（x）的定义域是{x|4+x>0且4-x＞0}={x|-4＜x＜4}，它具有对称性.因为f（-x）=lg（4-x）+lg（4+x）=f（x），所以f（x）是偶函数，不是奇函数.

综上可知，g（x）在（-∞，0）∪（0，+∞）上是奇函数.

变式1：已知函数f（x）为奇函数，且当x<0时，f（x）=x2+3x+2，则当x∈［1，3］时，f（x）的取值范围是______.

辨析：最后给出的两个变式，更进一步地将函数奇偶性运用于实战，这是公开课教学更注重实际的体现，也是近年来公开课教学的本真体现.在分段函数、复杂函数中，如何运用奇偶性概念成为思维更高层次的体现.变式1的具体解决：可以先求出x>0时，f（x）的解析式，再求当x∈［1，3］时，f（x）的取值范围，也可以直接求出当x∈［-3，-1］时，f（x）的取值范围，再利用奇函数的性质得到f（x）在［1，3］上的取值范围；变式2先将函数常数分离，得到数，根据奇函数的图像特点求解，不再赘述.

四、关注反思

公开课教学必须关注反思，每一堂 公开课都是教师综合素养能力的反映，因此哪些方面值得延续，哪些方面需要改进是很有思考价值的.总体来说，本课注重了下列几点，可以成为教学的一种模板：

其一，情境的有效性，本课情境是有效的，与后续知识的衔接是有价值的，不是为了情境而情境，这是笔者对于情境引入的一大收获.

其二，概念的建构是在教师引导下完成的，这才是符合中学生实际的，那些纯粹自身建构的伪探究是不符合教学实际的，这对于后续教师进一步思考公开课概念教学有相当大的思考.

其三，例题的选择需要层次性，层层递进符合了学生的认知规律，因此本课的例题设计和变式设计，对于学生思维的培养是有意的.

限于才疏学浅，本课在教学的立意和深度上还存在不足，请批评指正.