小议编题对于教师专业化成长的必要性

☉江苏省南通市通州区金沙中学 陈玲钰

众所周知，每年的高考真卷试题都是不少大学教授、中学教师合力创编的，其中不乏出产了很多优秀的试题.在为这样的试题叫好的同时，我们不禁要问，为什么一线教师更多的关心解题？却不太关心试题背后的命题机制？如何让教师从解题向编题、命题转变是提升教师专业化素养的关键.

一、概念理解的必要性

教师的成长需要两个环节，第一是教师自身对于概念的深入理解，第二是如何命制与概念相关的数学问题.不难发现，当下的数学教学对于概念教学的指导是乏力的、缺乏引导的，对于概念的一个定义、三项注意的教学方式依旧出现在诸多课堂的常态课教学中，这样的课堂教学首先说明了一个问题——教师自身没有深层次地理解数学概念，因此无法用自己的语言丰满地表述概念、阐述理解，只能通过大量的训练去替代，试问：这样的概念教学对于教师而言如何提高自身的专业化水准呢？没有深厚的概念理解，又如何去命制一个优秀的试题呢？因此教师自身对于数学概念的理解是必需的.

分析：最大值和最小值概念是数学必修1教材中提出的，教材中对于最值强调的是两个方面：其一，对任意定义域D中的自变量x，f（x）≤M成立；其二，必定存在x0∈D，使得f（x0）=M.笔者以为，学生并不了解这一概念的精髓，当且仅当才是最值概念最核心的理解.另一方面，最大值还有高等数学化的表述，即这种理解进一步提升了最值概念的代数化特征、抽象性，从而提高了学生的抽象思维和逻辑推理能力.

命题：已知定义在［0，2π］上的最大值函数f（x）=max{sinx，cosx}，最小值函数g（x）=min{sinx，cosx}，其中根为

考点分析：本题主要考查三角函数的图像与性质以及特殊值的运算，考查学生数形结合的能力，考查学生对问题的理解分析能力，该题运算量较大，综合性较强，有一定难度.

设计意图：要求学生画出正弦函数与余弦函数的图像，进一步得到最大值函数f（x）和最小值函数g（x）的图像，结合正余弦函数的性质计算x1，x2，x3，x4，然后再去检验选项的正确性.

我们易得正弦函数与余弦函数的图像，如图1.

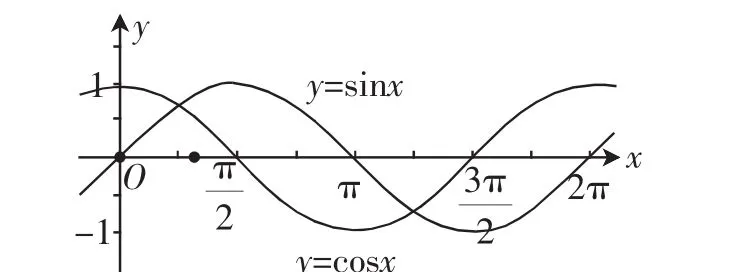
图1

得到最大值函数f（x）的图像，如图2.

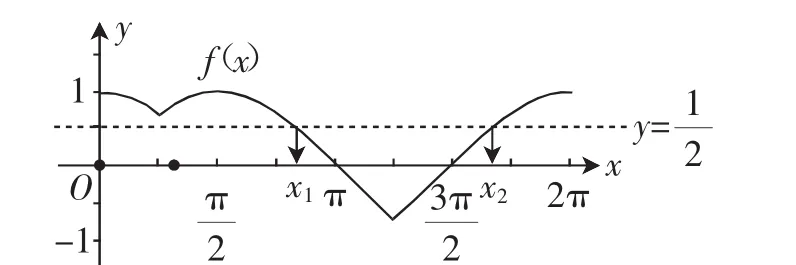
图2

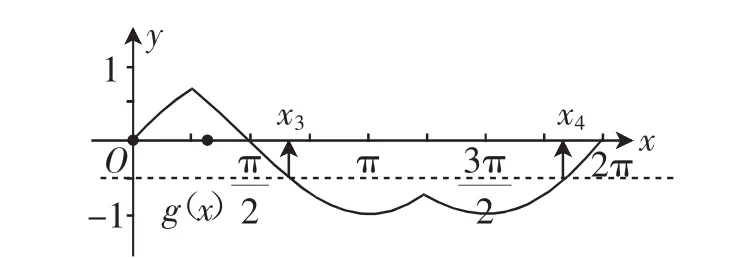
图3

说明：正确地理解最值概念，以及最值的高等数学表达符号，这都是对于最值概念最为深刻的理解，笔者以为在理解概念的基础上，结合自身教学经验，编制合理的试题有助于加深概念的理解，本题中对max{x，y}=两个符号的正确理解，并利用三角函数图像较为直观地区分学生对于最值的取舍，这是教师在自身理解最值概念基础上编制的数学问题，是以三角为背景的考查函数最值概念的基本问题，显得命题思路较为清晰.

二、寻求变式的必要性

变式教学是中国数学教育的重要特征之一，其大大提高了学生对于数学知识的理解力，因此变式教学往往对于学生理解数学有着重要的意义.在很多优秀的试题中，知识点的呈现往往连贯而经典，是多位老师通力合作的结果，对于教师而言，如何将这样的问题进一步改编呈现，对于学生来说，不仅了解命题的动向，也深刻地理解知识的内在，对于教师而言，大大加快了其自身专业化命题的素养.

图4

分析：如图4，不妨设△ABF2的边长为m，则|BF1|=m-2a，据双曲线的定义有：|AF1|=|AF2|+2a，所以m+m-2a=m+2a，即m=4a，|AF1|=6a，|AF2|=4a.在△AF1F2中，由余弦定理得|F1F2|2=（6a）2+（4a）2-2×6a×4acos60°，所以|F1F2|=

另法分析：如图5，不妨设BD=1，则AD=2，于是AC=3-2a，CD=1+2a.在△ACD中，由勾股定理得（1+2a）2=22+（3-2a）2，所以该双曲线的离心率为

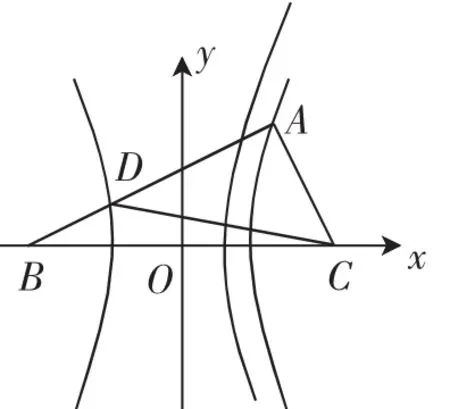
图5

说明：本题作为压轴题具有很好的区分度.本题主要考查双曲线的定义、离心率的求法及勾股定理.解法一使用坐标运算，利用点在双曲线上构造离心率方程求解；解法二借助双曲线定义和勾股定理求解，对比两种解法，明显第二种解法抓住了问题本质，运算量较小.改编本题的主要意图是让学生进一步理解：解决离心率问题的导向：首先思考椭圆、双曲线的定义，进一步理清蕴藏其中的平面几何性质，最后利用相关等式求解.

三、编制多解性问题的必要性

命题的另一个正确视角是编写的问题要有适度的多思维性，即可以从多视角入手，提高学生对于知识理解的全面性，这种全面性依托了教师对于问题的合理命制，以及从知识点角度对于问题的考虑.解题大师罗增儒教授说：解题要解透一道题，而不是关注其数量的多少，解透一道题必然要考虑试题的多角度解答，这样对于教师的成长是快速的.笔者以为，对于学生而言也是一并如此，因此命制更好的试题成为多解性问题探索的条件.

问题：如图6，已知圆C：x2+（y-2）2=5，A（-1，0），M是圆C的弦AB的中点，且|OA|=|OM|.则直线AB的斜率为_______.

分析：本题为笔者原创题，主要在圆的垂径定理上设计关系.所以解法2将两个垂直条件结合，直接秒杀该题.若不能看出其中的垂直关系，也能经过运算求解，这便是解法1.

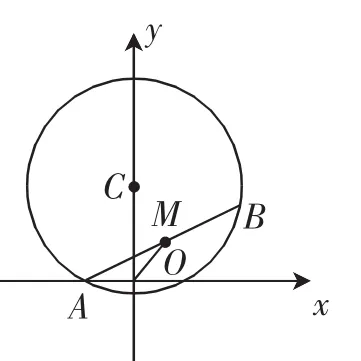
图6

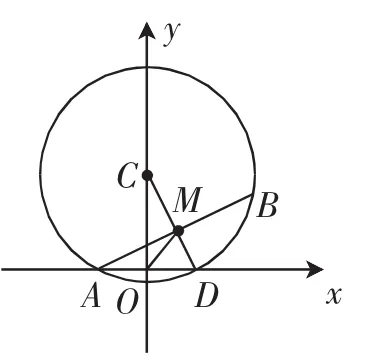
图7

解法2：如图7所示，连接MC，MD.

说明：中学数学问题的解决显然是两个主要视角，其一是代数化的视角，本题解法1自然是注重学生的代数运算的能力，因此在学生日益缺乏运算能力的时候，平时关注代数视角是不错的选择；其二是几何直观，可以这么说，中学数学的几个典型章节，都是以几何为主的解法占据了优势，譬如向量、直线和圆、抛物线问题、椭圆双曲线离心率问题、函数图像问题等，因此命制本题恰恰是双管齐下的复习数学问题解决的两个主要导向——代数和几何.

总之，编题是教师成长路上不可或缺的环节，要如何编题、编什么样的问题，这是值得教师不断思考和总结的.笔者以为，以高考真卷为参考，编制以概念理解为导向的试题是第一选择，以高考真卷问题改编是第二选择，以一题多解的命制为第三选择，长此以往，对于教师自身命题能力的提高有着重要的作用，成为专业化成长的关键之一.