零膨胀Poisson分布模型回归分析

胡良平

(1.军事科学院研究生院，北京 100850； 2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

1 零膨胀计数资料及其零膨胀Poisson分布回归模型构建原理

1.1 零膨胀计数资料Poisson分布回归模型的形式

1.1.1适于零膨胀计数资料Poisson分布回归模型的数据结构

适于零膨胀计数资料Poisson分布模型的数据结构见表1。

【对数据结构的分析】因变量count为“计数变量”，它是“鱼的条数”。不难发现，没有钓到鱼的人数很多，或者说，count=0出现的频数很多，这种现象被称为“零膨胀”或“零堆积”。显然，钓鱼者的“性别”“年龄”可被视为两个自变量。

1.1.2零膨胀计数资料Poisson分布回归模型的表达式

在零膨胀Poisson(简称ZIP)分布回归模型中，早期定义的数据产生过程被称为“过程2”，即Poisson分布概率函数，由下面的式(1)给出：

(1)

(2)

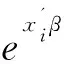
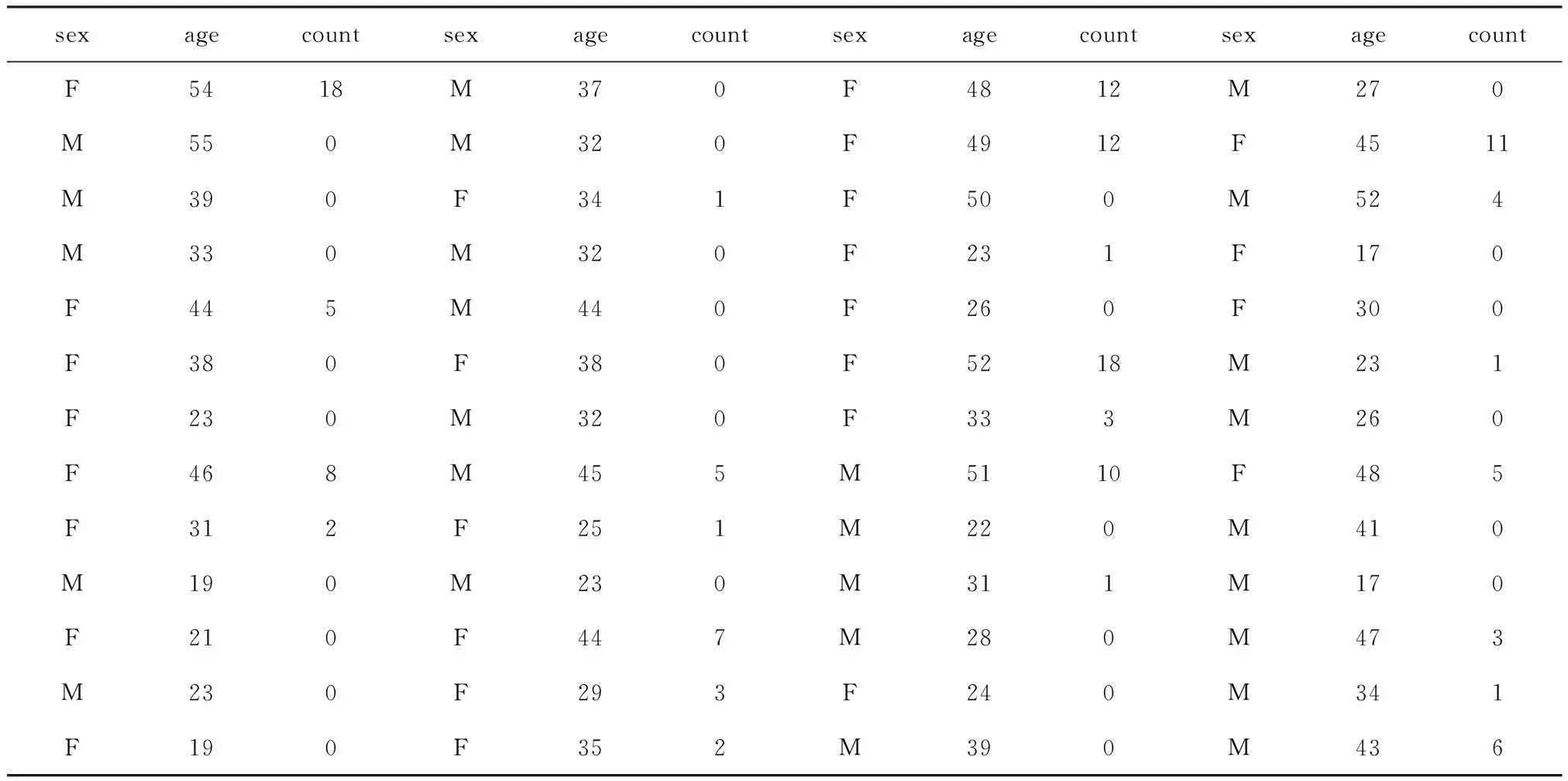
表1 研究者随机调查在某公园钓鱼的52人的性别、年龄和过去半年内钓鱼条数

注：sex，性别；age，年龄(岁)；count，鱼的条数；F，女；M，男；此资料取自SAS 9.3的“帮助信息”，具体来说，取自SAS/STAT的“FMM过程”中的“getting started”中的第2个例子

yi的条件期望(或均值)与条件方差分别见下面的式(3)与式(4)：

E(yi|xi,zi)=μi(1-Fi)

(3)

V(yi|xi,zi)=E(yi|xi,zi)(1+μiFi)

(4)

值得注意的是，比较式(4)与式(3)可知，方差大于均值，故ZIP回归模型(也包括ZINB回归模型，即零膨胀负二项分布回归模型)刻划的是具有“零堆积”且具有“过离散”现象的计数因变量随自变量变化而变化的依赖关系。

1.2 零膨胀计数资料Poisson分布回归模型的求解

1.2.1 求解参数的思路

如何求解出式(2)中的概率“Fi”和回归系数“βi”呢？与大多数“广义线性模型”[1-2]求解思路大同小异，其常规做法如下：第1步，基于“最大似然原理”并利用“概率函数(对离散型随机变量而言)或概率密度函数(对连续型随机变量而言)”构建“目标函数”，即所谓的“似然函数”；第2步，求取似然函数的自然对数L；第3步，求取L关于参数的一阶和二阶偏导数；第4步，令二阶偏导数为“0”，得到方程组；第5步，采用某种迭代计算方法，求出方程组的解，即求得参数的估计值。

1.2.2零膨胀Poisson分布回归模型的自然对数似然函数

概括地说，ZIP回归模型的自然对数似然函数具有下面的形式，见式(5)：

(5)

在一个被指定的连接函数(即Logistic分布函数或标准正态分布函数)用于概率Fi之后，就可以写出自然对数似然函数与其导数的精确表达式。

1.2.3用Logistic分布函数作为连接函数的ZIP回归模型及参数估计

首先，考虑在ZIP回归模型中用Logistic分布函数作为连接函数来表达概率Fi，这个函数就是下面的式(6)：

(6)

此时，ZIP回归模型的自然对数似然函数见下面的式(7)：

(7)

式(7)中的“wi”为“权重系数”，视具体情形而定，大体可分为以下6种情形：

(1)wi=1

当数据集中没有可作为“权重”变量或“频数”变量及其取值时，就令“wi=1”。

(2)wi=Wi

当用户在“WEIGHT语句”中指定了“非正态化”选项，而且，在“WEIGHT语句”中指定了变量及其非正态化取值时，就令“wi=Wi”。

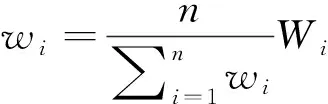
(4)wi=Fi

在“FREQ语句”中，指定了变量及其取值Fi时，就令“wi=Fi”。

(5)wi=WiFi

当用户在“WEIGHT语句”中没有使用“非正态化”选项，而且，同时使用了“WEIGHT语句”和“FREQ语句”，当然，Wi和Fi分别为前面提及的两个语句中变量的取值，就令“wi=WiFi”。

对于ZIP回归模型的偏导数分别见下面的式(8)和式(9)：

(8)

(9)

1.2.4用标准正态分布函数作为连接函数的ZIP回归模型及参数估计

首先，考虑在ZIP回归模型中用标准正态分布函数作为连接函数来表达概率，这个函数就是下面的式(10)：

(10)

此时，ZIP回归模型的自然对数似然函数见下面的式(11)：

(11)

式(11)中对“wi的定义同式(7)，此处从略。

对ZIP回归模型的偏导数分别见下面的式(12)和式(13)：

(12)

(13)

【说明】以上计算公式来源于SAS/ETS模块中“COUNTREG过程”的“details”部分。

1.2.5 二阶偏导数及迭代计算

通常情况下，需要在一阶偏导数的基础上，求取二阶偏导数；进而，令各参数的二阶偏导数及二阶混合偏导数为“0”，形成方程组。再利用某种迭代计算方法，从而求出各参数的估计值。因篇幅所限，详细做法此处从略。

2 零膨胀Poisson分布回归模型的SAS实现

2.1 创建SAS数据集

利用下面的SAS数据步程序，创建名为“catch”的临时SAS数据集：

data catch;

input gender $ age count @@;

if gender=' F ' then sex=0;

else if gender=' M ' then sex=1;

datalines;

2.2 编制出因变量count的频数分布表并绘制出其频数分布直条图

利用下面的一个SAS过程步程序，编制出因变量count的频数分布表，并绘制出其频数分布直条图(因为count是离散型随机变量，只取“0”和“非0正整数”值)：

proc freq data=catch;

tables count/out=aaa plots=freqplot;

run;

【SAS输出结果】

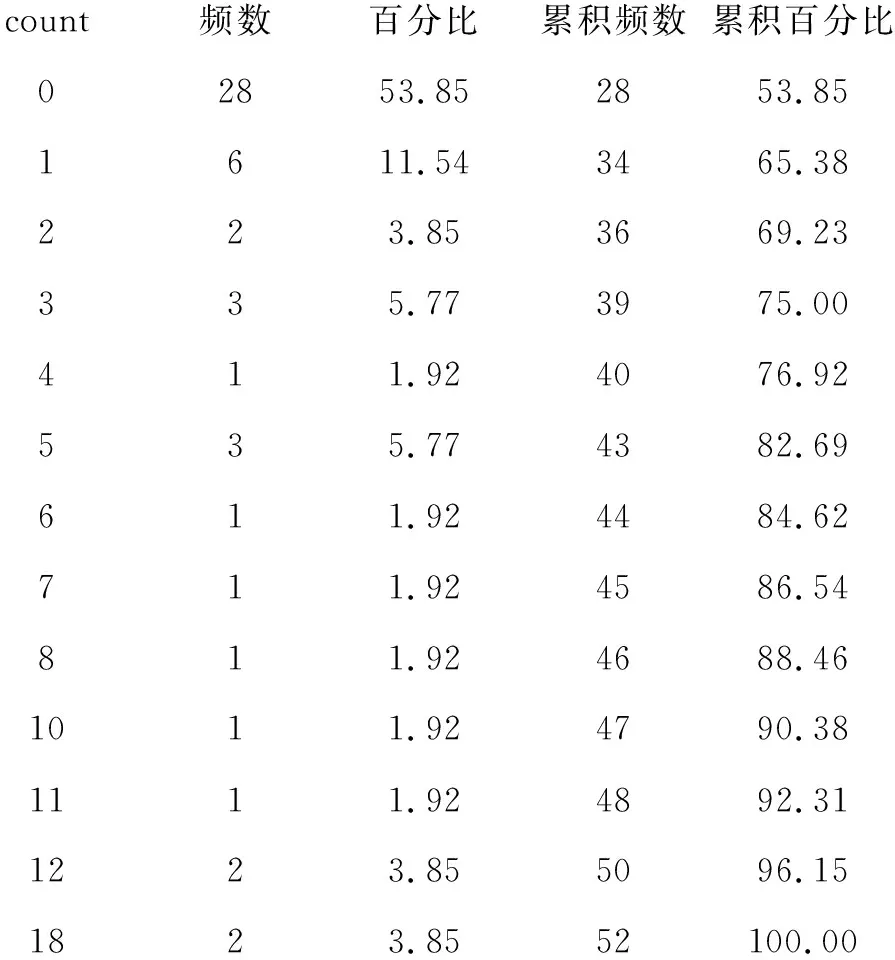
count频数百分比累积频数累积百分比02853.852853.851611.543465.38223.853669.23335.773975.00411.924076.92535.774382.69611.924484.62711.924586.54811.924688.461011.924790.381111.924892.311223.855096.151823.8552100.00

以上是计数因变量count的频数分布表，count=0出现的频数为28，占总频数52的53.85%。

以下是“计数因变量count的频数分布直条图”，见图1。

图1 计数因变量count的频数分布直条图

图1直观、形象地呈现出计数因变量count取“0”的频数非常多，这种现象被称为“零膨胀”或“零堆积”。

2.3 求出因变量count的均值和方差

利用下面的两个SAS过程步程序，求出除“0”之外的其他计数资料的方差和均值：

proc univariate data=catch(where=(count ne 0)) noprint;

var count;

output out=aaa mean=mfish var=vfish;

run;

proc print data=aaa;

run;

【SAS输出结果】

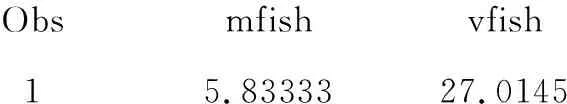
Obsmfishvfish15.8333327.0145

求得除“0”之外的其他计数因变量的均值为5.83333、方差为27.0145，方差约为均值的4.63倍。

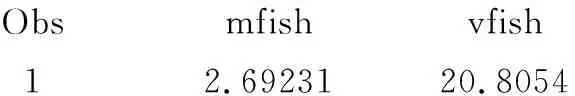
Obsmfishvfish12.6923120.8054

以上是基于计数因变量count的全部52个观测值计算所得到的均值和方差，方差约为均值的7.73倍。

由此可知，此计数资料属于“过离散计数资料”。

2.4 基于全部自变量对因变量count构建多重零膨胀Poisson分布回归模型

2.4.1利用下面的SAS过程步程序尝试性构建多重Poisson分布回归模型

/*仅拟合多重Poisson分布回归模型*/

proc fmm data=catch;

class gender;

model count=gender*age/dist=Poisson;

run;

【SAS输出结果】

Fit Statistics-2 Log Likelihood 182.7AIC (smaller is better)188.7AICC (smaller is better)189.2BIC (smaller is better)194.6 Pearson Statistic85.9573

关于模型对资料的拟合效果，暂不评价，需要与其他同类模型的拟合结果进行比较，才能得出有说服力的判定。

2.4.2利用下面的SAS过程步程序尝试性构建多重负二项分布回归模型

/*仅拟合多重负二项分布回归模型*/

proc fmm data=catch;

class gender;

model count=gender*age/dist=nb;

run;

【SAS输出结果】

Fit Statistics-2 Log Likelihood162.1AIC (smaller is better)170.1AICC (smaller is better)171.0BIC (smaller is better)177.9 Pearson Statistic38.3597

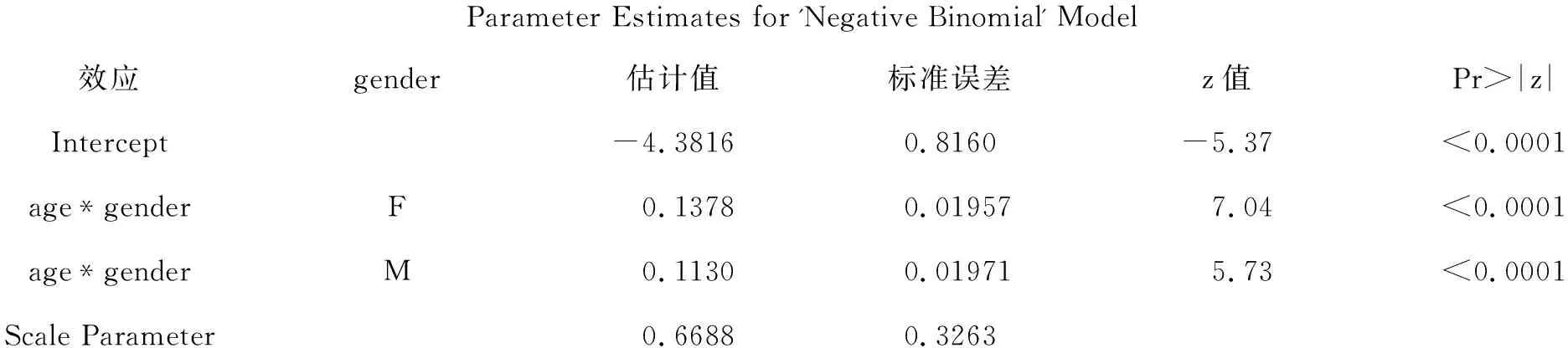
Parameter Estimates for 'Negative Binomial' Model效应gender估计值标准误差z值Pr>|z|Intercept-4.38160.8160-5.37<0.0001age*genderF0.13780.019577.04<0.0001age*genderM0.11300.019715.73<0.0001Scale Parameter0.66880.3263

比较以上两个统计模型给出的“拟合统计量”部分结果可知，“多重负二项分布回归模型”好于“多重Poisson分布回归模型”，因为AIC、AICC、BIC和“Pearson Statistic(皮尔逊卡方统计量)”数值均有所下降。

2.4.3利用下面的SAS过程步程序构建多重零膨胀Poisson分布回归模型

(1)按性别分层且基于常数与Poisson分布分别拟合零膨胀与非零膨胀两部分的零膨胀Poisson分布回归模型

proc fmm data=catch;

class gender;

model count = gender*age / dist=Poisson;

model + / dist=Constant;

run;

【SAS主要输出结果】

Fit Statistics-2 Log Likelihood145.6AIC (smaller is better)153.6AICC (smaller is better)154.5BIC (smaller is better)161.4Pearson Statistic43.4467Effective Parameters4Effective Components2

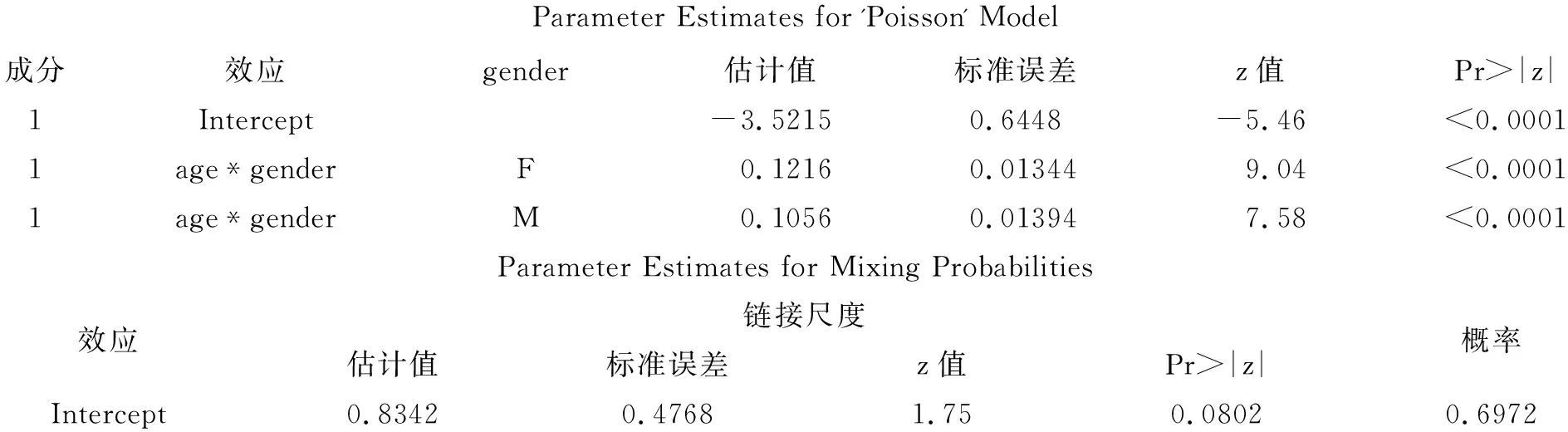
Parameter Estimates for 'Poisson' Model成分效应gender估计值标准误差z值Pr>|z|1Intercept-3.52150.6448-5.46<0.00011age*genderF0.12160.013449.04<0.00011age*genderM0.10560.013947.58<0.0001Parameter Estimates for Mixing Probabilities效应链接尺度估计值标准误差z值Pr>|z|概率Intercept0.83420.47681.750.08020.6972

关于模型对资料的拟合效果，暂不评价，需要与其他同类模型的拟合结果进行比较，才能得出有理由的判定。若仅依据“AIC、AICC、BIC”的数值来判断，要好于前面的“多重负二项分布回归模型”的拟合效果。

(2)不按性别分层且基于常数与Poisson分布分别拟合零膨胀与非零膨胀两部分的零膨胀Poisson分布回归模型

proc fmm data=catch;

class gender;

model count = gender age / dist=Poisson;

model + / dist=Constant;

run;

【SAS主要输出结果】

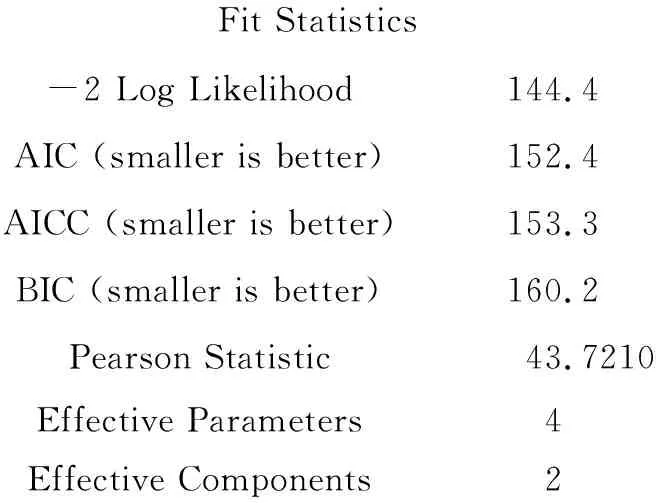
Fit Statistics-2 Log Likelihood144.4AIC (smaller is better)152.4AICC (smaller is better)153.3BIC (smaller is better)160.2Pearson Statistic43.7210Effective Parameters4Effective Components2

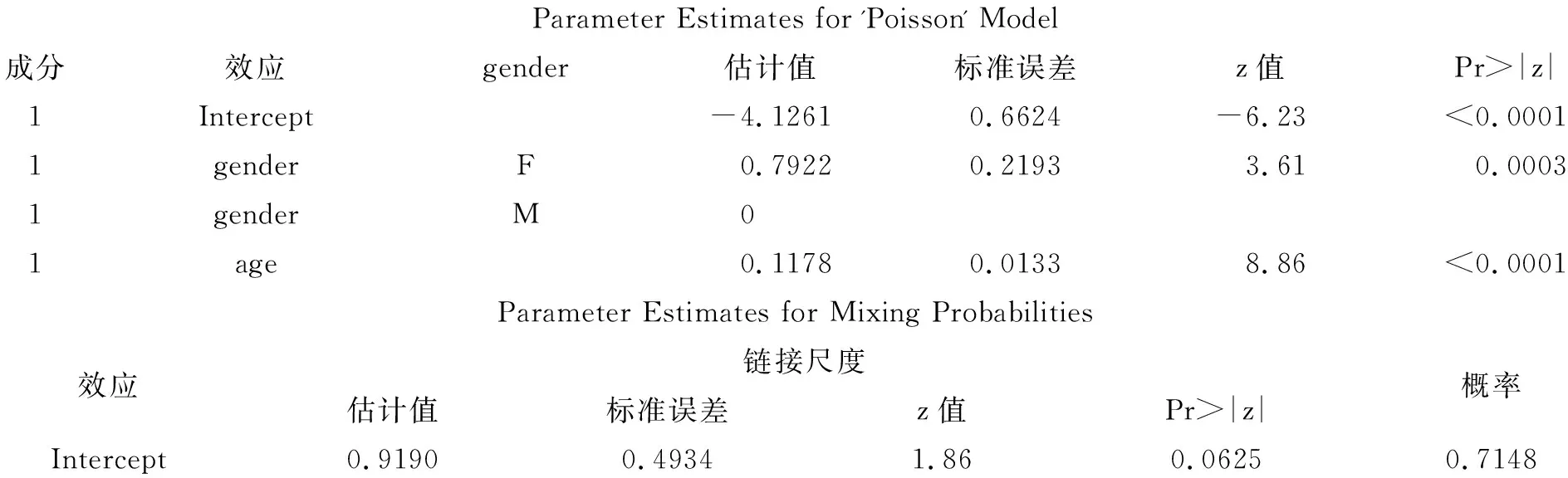
Parameter Estimates for 'Poisson' Model成分效应gender估计值标准误差z值Pr>|z|1Intercept-4.12610.6624-6.23<0.00011genderF0.79220.21933.610.00031genderM01age0.11780.01338.86<0.0001Parameter Estimates for Mixing Probabilities效应链接尺度估计值标准误差z值Pr>|z|概率Intercept0.91900.49341.860.06250.7148

若仅依据“AIC、AICC、BIC”的数值来判断，要略好于前面“按性别分层”的拟合效果，但二者无差异。

2.5 最终的回归模型与专业结论

2.5.1 最终的回归模型

依据上面最后一次选定的回归模型拟合资料所得到的计算结果写出“多重零膨胀Poisson分布回归模型”，此模型由两个表达式组成，一个对应于“yi=0”；另一个对应于“yi>0”。模型表达式见前面的式(2)，其中，Fi=0.7148、μi=e-4.1261+0.7922(sex=F)+0.1178age。将这两个参数的估计结果代入式(2)，就可获得与表1资料对应的“零膨胀Poisson分布回归模型”。

2.5.2 专业结论

任何一人钓不到鱼的概率约为71.5%(因上面第一式“加号”后面与钓鱼者性别、年龄有关，但其数值并不大)；女性较男性、年龄长者较年龄小者钓鱼数目多。