过离散计数资料负二项分布模型回归分析

胡良平

(1.军事科学院研究生院，北京 100850； 2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

1 过离散计数资料及其负二项分布模型构建原理

1.1 适于过离散计数资料负二项分布回归模型的数据结构

适于过离散计数资料负二项分布模型的数据结构见表1[1]。

表1数据来自德国的卫生改革项目。改革的目的是减少患者到医生处的就诊次数。数据共包括2 227例观测，分别属于改革之前的1996年和改革之后的1998年。响应变量为患者在3个月之内的就诊次数，自变量为改革前后(0=改革前，1=改革后)、健康状况(0=良好，1=不良)、年龄、受教育时间和家庭收入的对数值。由于数据量较大，表1中仅列出部分结果。求出“就诊次数”的均值与方差如下。

均值方差12.5891316.1299

【对数据结构的分析】因变量Y“就诊次数”为“计数变量”，其均值为2.589、方差为16.130，方差明显大于均值，只能将Y视为服从负二项分布的离散型随机变量；拟考察的四个自变量中，有两个是“二值变量”，另外两个是“计量变量”。虽然，在统计学的理论上，默认自变量全为“计量变量”，但从实用性角度出发，“二值”自变量也是可以接受的。

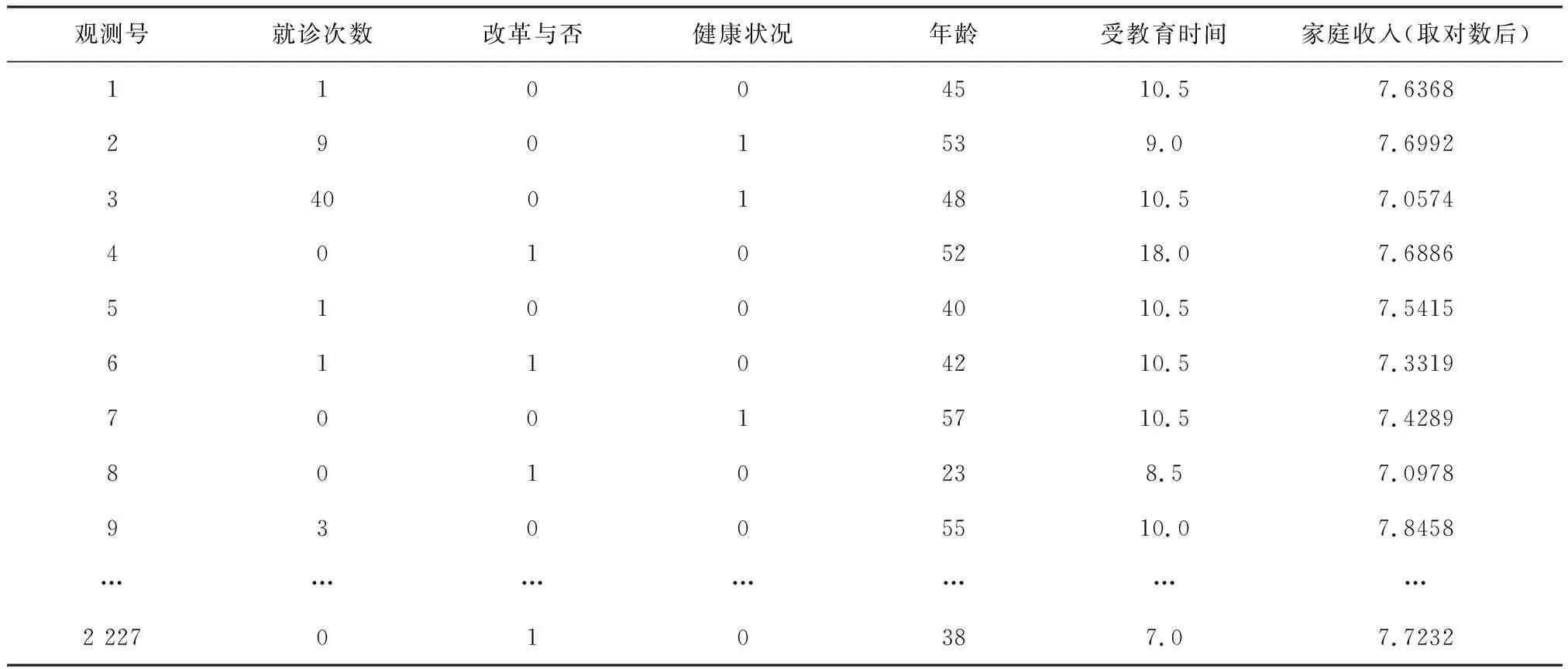
表1 患者就诊次数及其影响因素数据

1.2 过离散计数资料负二项分布回归模型的构建与求解[2]

1.2.1 Poisson分布回归模型的推广

在对第i个个体进行观测时，通过引入一个观测不到的非齐性项“τi”，从而使Poisson分布回归模型得到推广。因此，假定个体之间以随机的方式呈现彼此的差异，原因在于可观测的协变量不能完全解释不同个体之间实际存在的差异。此种情况可用如下的式子来呈现，见式(1)：

(1)

在式(1)中，观测不到的非齐性项τi=eεi独立于自变量向量xi。于是，yi关于xi和τi的条件分布是关于条件均值和条件方差均为μiτi的Poisson分布，其概率函数见式(2)：

(2)

令g(τi)为τi的概率密度函数，于是，通过对f(yi|xi,τi)求关于τi的积分，便可求得f(yi|xi)的概率分布，见式(3)：

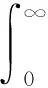
(3)

在式(3)中，当假定τi服从伽玛分布时，其积分的结果存在解析解，这个解就是负二项分布。

为了确定分布的均值，当模型中包含常数项时，必需假定E(eεi)=E(τi)=1。因此，假定τi为服从gamma(θ,θ)分布且其均值和方差分别为E(τi)=1和V(τi)=1/θ，其概率密度函数见式(4)：

(4)

在式(4)中，分母中的伽玛函数见式(5)：

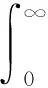
(5)

而式(4)中的θ是一个正的参数。

1.2.2 负二项分布概率函数形式之一

于是，在给定了xi的条件下，推导出yi的概率函数见式(6)：

(6)

1.2.3 负二项分布概率函数形式之二

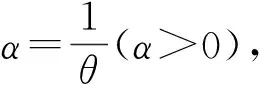
yi=0,1,2…

(7)

因此，负二项分布概率函数是由服从Poisson分布与伽玛分布的两类随机变量混合而成的。其条件均值和条件方差分别见式(8)和式(9)：

(8)

(9)

由式(9)可知，负二项分布的条件方差明显大于其条件均值，这种“过离散”的结果是忽视未观测到的非齐性项所致。

式(9)显示出：负二项分布的方差函数是其均值的二次方，这个结果可被称为第2种定义下的负二项分布回归模型(即“Cameron and Trivedi 1986”)，简称为“2型负二项分布回归模型”。当α=0时，负二项分布就退化成为Poisson分布了。检验“α=0”这个假设是否成立，可使用WALD检验。

1.2.4 2型负二项分布回归模型的自然对数似然函数及一阶偏导数

2型负二项分布回归模型的自然对数似然函数可由下面的式(10)给出：

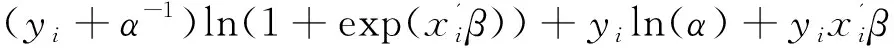
(10)

在式(10)中，wi的定义很繁琐，参见有关文献，此处从略；在式(10)等号右边第二个求和号之后的第一项是怎么得到的？它是由如下的原因所致：在式(7)中，两个伽玛函数相除可以改写成乘积形式，见下面的式(11)：

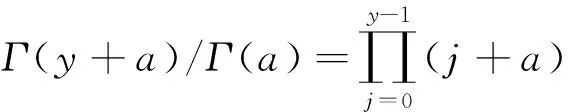
(11)

基于式(10)，求L关于参数β的偏导数，见下面的式(12)：

(12)

基于式(10)，求L关于参数α的偏导数，见下面的式(13)：

(13)

1.2.5 1型负二项分布回归模型的自然对数似然函数及一阶偏导数

V(yi|xi)=μi+αμi

(14)

为了估计这样的模型，在“model语句”中指定“DIST=NEGBIN(p=1)”这样的选项。

于是，1型负二项分布回归模型的自然对数似然函数由下面的式(15)给出：

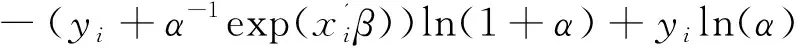
(15)

在式(15)中，wi为权重系数，其定义视具体情况而定，因篇幅所限，此处从略。

基于式(15)，求L关于参数β的偏导数，见下面的式(16)：

α-1ln(1+α)μixi}

(16)

基于式(15)，求L关于参数β的偏导数，见下面的式(17)：

(17)

1.2.6 二阶偏导数及迭代计算

通常情况下，需要在一阶偏导数的基础上，求取二阶偏导数；进而，令各参数的二阶偏导数及二阶混合偏导数为0，形成方程组。再利用某种迭代计算方法，从而求出各参数的估计值。因篇幅所限，详细做法此处从略。

2 过离散计数资料负二项分布回归模型的SAS实现[3]

2.1 创建SAS数据集

利用下面的SAS数据步程序，创建名为“nbd1”的SAS数据集：

data nbd1;

infile 'd:SASTJFXmdvisit.dat';

input id numvisit reform badh age edu loginc;

run;

【SAS程序说明】将本例中全部2 227行数据(注意：表1中仅列出了前9行和最后一行)录入计算机，以“文本格式”且以“mdvisit.dat”为文件名，存储在名为“SASTJFX”的D盘文件夹内。每行有7个数据，分别为“编号(id)”“三个月内的就诊次数(numvisit)”“改革前后(reform)(0=改革前，1=改革后)”“健康状况(badh)(0=良好，1=不良)”“年龄(age)”“受教育时间(edu)”和“家庭收入的对数值(loginc)”。

2.2 求出因变量numvisit的均值和方差

利用下面的两个SAS过程步程序，求出因变量Y的均值和方差：

proc univariate data=nbd1 noprint;

var numvisit;

output out=aaa mean=ybar var=yvar;

run;

proc print data=aaa;

var ybar yvar;

run;

【SAS输出结果】

Obsybaryvar12.5891316.1299

求出3个月内就诊次数(numvisit)的均值和方差分别为2.589和16.130。此结果表明，方差约为均值的6.23倍，属于较严重的“过离散”。

2.3 基于全部自变量对因变量Y构建多重Poisson分布回归模型

利用下面的SAS过程步，尝试构建Poisson分布回归模型，目的是为了使用选项“noscale”进行拉格朗日乘子检验，以明确是否存在明显的“过离散”现象。

proc genmod data=nbd1;

model numvisit= reform badh age edu loginc/link=log dist=nb noscale;

run;

【SAS程序说明】“link=log”表明采用“自然对数”作为联接函数，即对计数因变量取自然对数变换；“dist=nb”表明要基于负二项分布构建负二项分布回归模型。但是，选项“noscale”的作用是将冗余参数k的取值固定为“0”，此时，相当于构建Poisson回归模型。与此同时，该选项的主要用途是进行拉格朗日乘子检验，以明确因变量是否存在明显的“过离散”现象。

【SAS主要输出结果】基于Poisson分布回归模型的参数估计结果没有实用价值，此处从略。

拉格朗日乘数统计量参数卡方Pr > 卡方离散度551.7077<.0001*

注：*单侧P值

以上结果表明，因变量存在极严重的“过离散”现象。

2.4 尝试对“过离散”现象进行校正后再构建Poisson分布回归模型

利用下面的SAS过程步程序对“过离散”现象进行校正后再构建Poisson分布回归模型：

proc genmod data=nbd1;

model numvisit= reform badh age edu loginc/link=log dist=poisson scale=deviance;

run;

【SAS程序说明】选项“scale=deviance”是要求对“过离散”进行校正后，再构建Poisson分布回归模型。

【SAS主要输出结果】

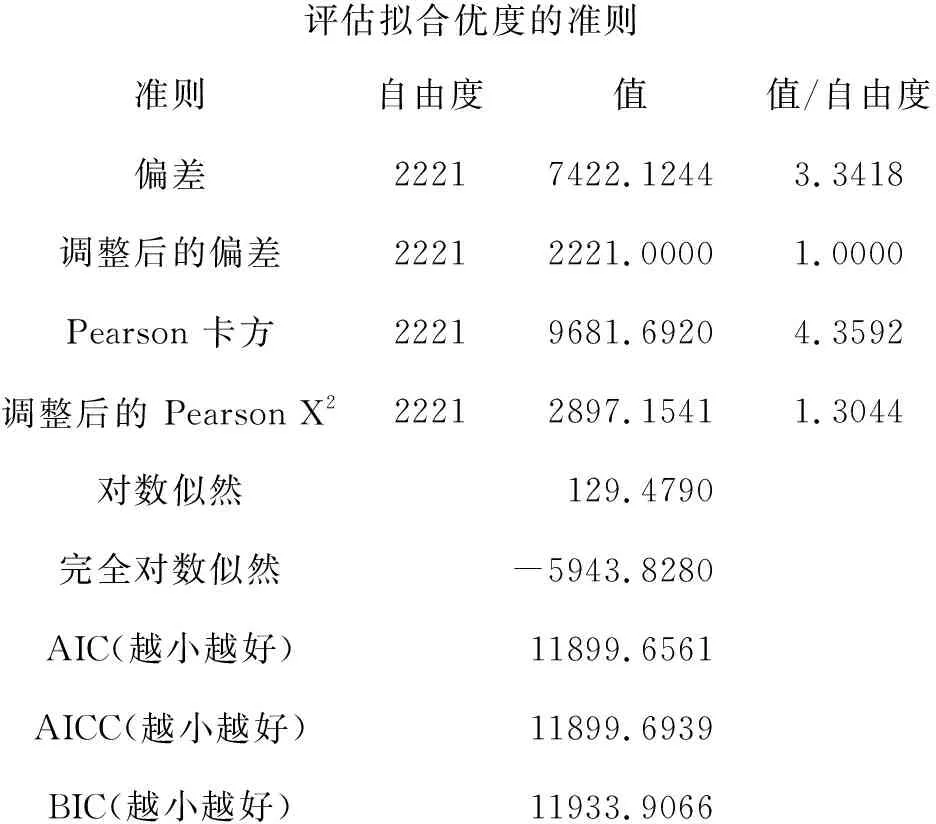
评估拟合优度的准则准则自由度值值/自由度偏差22217422.12443.3418调整后的偏差22212221.00001.0000Pearson 卡方22219681.69204.3592调整后的 Pearson X222212897.15411.3044对数似然129.4790完全对数似然-5943.8280AIC(越小越好)11899.6561AICC(越小越好)11899.6939BIC(越小越好)11933.9066

以上是采用Poisson分布回归模型拟合此资料所对应的“拟合优度”评价指标及其取值，这些结果需要与其他同类模型比较，才有价值。

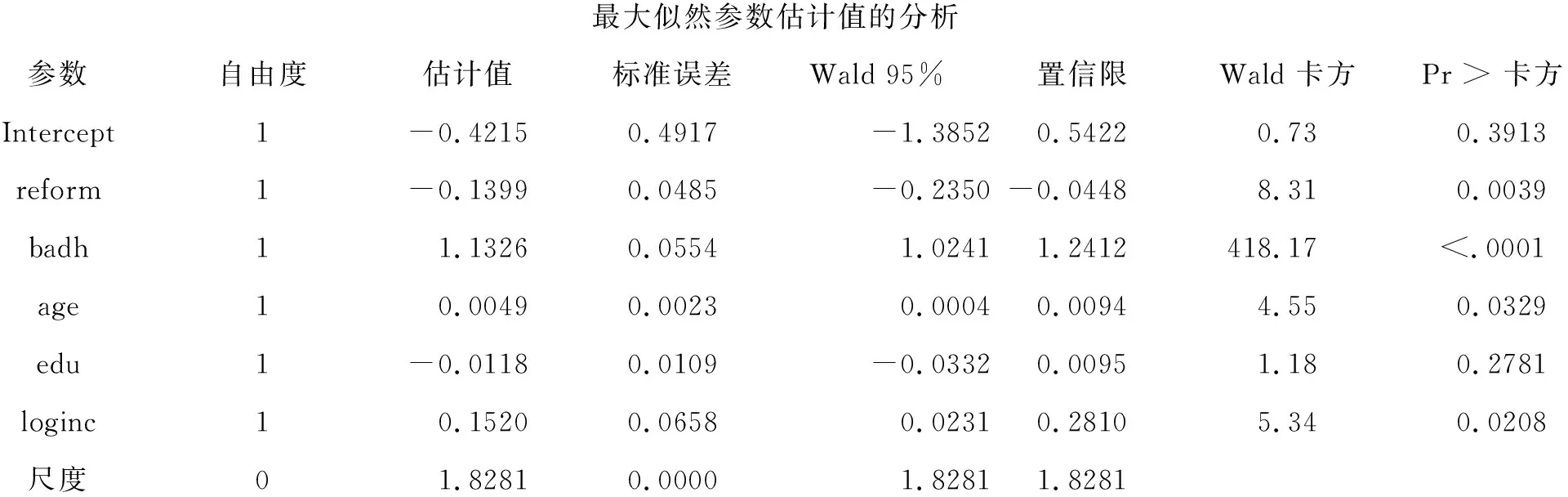
最大似然参数估计值的分析参数自由度估计值标准误差Wald 95%置信限Wald 卡方Pr > 卡方Intercept1-0.42150.4917-1.38520.54220.730.3913reform1-0.13990.0485-0.2350-0.04488.310.0039badh11.13260.05541.02411.2412418.17<.0001age10.00490.00230.00040.00944.550.0329edu1-0.01180.0109-0.03320.00951.180.2781loginc10.15200.06580.02310.28105.340.0208尺度01.82810.00001.82811.8281

Note: The scale parameter was estimated by the square root of DEVIANCE/DOF

最后一行“注释”的含义是：尺度参数是“离差/自由度”的平方根，即(7422.124/2221)的平方根，其数值为1.8281。

以上结果表明：尺度参数由原先的“1”调整为“1.8281”，由此，模型中各参数的“标准误”都得到“校正”。从而，最后两列的数值也都得到校正。

2.5 在“过离散”现象严重的情况下构建多重负二项分布回归模型

proc genmod data=nbd1;

model numvisit= reform badh age edu loginc/link=log dist=nb;

run;

【SAS主要输出结果】

评估拟合优度的准则准则自由度值值/自由度偏差22212412.34641.0862调整后的偏差22212412.34641.0862Pearson 卡方22212693.55141.2128调整后的 Pearson X222212693.55141.2128对数似然1813.1299完全对数似然-4563.3905AIC(越小越好)9140.7809AICC(越小越好)9140.8314BIC(越小越好)9180.7398

以上“拟合优度评价指标的取值”与前面基于“Poisson分布回归模型”的相应评价指标的取值相比，现在的模型，即“负二项分布回归模型”对此资料的拟合效果好多了(偏差变小了，AIC、AICC和BIC都变小了很多)。

以上结果表明，截距项无统计学意义，去掉截距项后，可使模型精简一些。

2.6 构建不含截距项且删除无统计学意义的自变量edu的负二项分布回归模型

proc genmod data=nbd1;

model numvisit= reform badh age loginc/noint link=log dist=nb;

run;

【SAS主要输出结果】

与前面的结果相比，拟合优度评价指标的取值又有所改善。

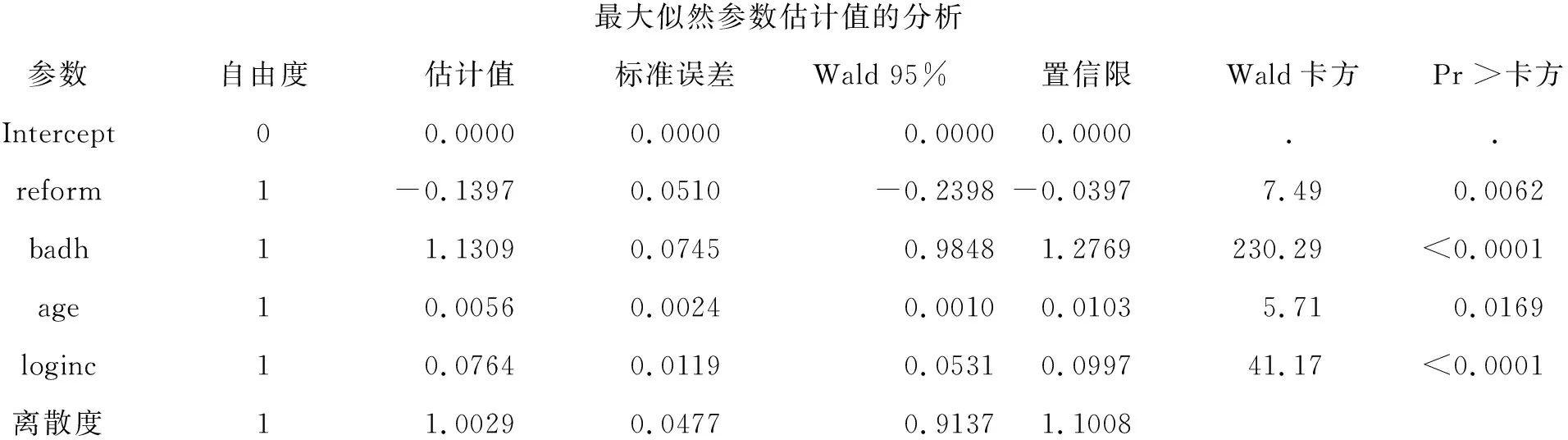
最大似然参数估计值的分析参数自由度估计值标准误差Wald 95%置信限Wald卡方Pr >卡方Intercept00.00000.00000.00000.0000..reform1-0.13970.0510-0.2398-0.03977.490.0062badh11.13090.07450.98481.2769230.29<0.0001age10.00560.00240.00100.01035.710.0169loginc10.07640.01190.05310.099741.17<0.0001离散度11.00290.04770.91371.1008

基于以上的结果可以写出最终的负二项分布回归模型的“内核”，如下：

ln[μ(X)]=-0.1397reform+1.1309badh+0.0056age+0.0764loginc

μ(X)=e-0.1397reform+1.1309badh+0.0056age+0.0764loginc

若将上面“μ(X)”等号后面的内容代入式(6)或式(7)，便可获得多重负二项分布回归模型的完整表达式。

【专业结论】改革与否、健康状况和年龄这三个因素对患者就诊次数的影响具有统计学意义，结合参数估计的结果来看：改革与否的系数为-0.1397，说明改革之后，患者的就诊次数下降了。具体地说，因exp(-0.1397)=0.869619，即就诊次数下降了约1-0.869619=13.04%；相对于良好健康状况、年龄小的患者，具有不良健康状况、年龄大均会使就诊次数增加(因为它们的回归系数为正值)。