Effects of Landau damping and collision on stimulated Raman scattering with various phase-space distributions

Shanxiu Xie(谢善秀) Yong Chen(陈勇) Junchen Ye(叶俊辰)

Yugu Chen(陈雨谷)1, Na Peng(彭娜)1, and Chengzhuo Xiao(肖成卓)1,3,†

1Key Laboratory for Micro-/Nano-Optoelectronic Devices of Ministry of Education,School of Physics and Electronics,

Hunan University,Changsha 410082,China

2Institute of Applied Physics and Computational Mathematics,Beijing 100094,China

3Collaborative Innovation Center of IFSA(CICIFSA),Shanghai Jiao Tong University,Shanghai 200240,China

Keywords: stimulated Raman scattering,Landau damping,distribution functions

1. Introduction

Stimulated Raman scattering(SRS),in which an incident laser decays into a scattered light wave and a Langmuir wave,is one of the most significant instabilities in inertial confinement fusion (ICF). It can not only scatter the pump energy,but also produce hot electrons,[1–3]degrading the implosion of fuel capsule.Therefore,understanding the evolution of SRS in the whole stage of laser plasma interaction, during which the distribution of plasma changes,is crucial for controlling SRS to an acceptable level.

It is well-known and well-understood that SRS is often triggered in an equilibrium plasma, or the so-called Maxwellian distributed plasma. Research in early years was mostly based on the Maxwellian distribution functions, such as the use of fluid equations.[4–6]However,researchers found that modification of the distribution function due to nonlinear evolution of SRS has non-negligible effects on SRS. Using kinetic simulations, Vuet al.revealed that when particles are trapped, it changes the Landau damping of Langmuir wave, which then leads to an inflation of SRS.[7,8]The trapped-particle distribution function always has an plateau near the phase velocity of Langmuir wave. This modified distribution function can trigger new wave modes other than the Langmuir wave in the Maxwellian distribution, such as the beam acoustic mode(BAM)[9–11]and the electron acoustic wave(EAW),[12–16]and it also evolves to new trapping induced nonlinearities, such as nonlinear frequency shift,[7,17]modulation instability,[18,19]sideband instability,[20–23]wavefront bowing,[24]etc.

There remain fundamental questions on the evolution of SRS in such phases, e.g., how does SRS response to these modified plasma distribution functions and what is the essential role of Landau damping acting in these processes?For Maxwellian distribution, the SRS growth rate and Landau damping are well-known. For trapped-particle distribution, there are several individual models calculating the Landau damping and explaining its role in the SRS.[36–39]However, they all applied to fluid models and no kinetic simulations are discussed. While for the bi-Maxwellian distribution,its effect on SRS is seldom studied,except that Roseet al.[40]studied the Landau damping under such distribution functions.In addition, collisions are considered to be ignored in many cases for it is always considered small. Nevertheless,in 1958,Lenardet al.were among the first works to study the effect of collisions on Landau damping using a Fokker–Planck-type equations.[41]In 1992,Epperleinet al.have shown that collisions increase the damping.[42]In 2003,Penget al.proposed that the presence of collisions in the high electron density region greatly reduces the growth of SRS.[43]These prompted us to include the collision term in this paper to consider its impact on our research.

Therefore, in this paper we study the relationship between Raman growth and Landau damping with different distribution functions which occur in three representative stages:Maxwellian distribution representing the very early stage of SRS, flattened distribution aimed at showing effects of particle trapping, and bi-Maxwellian distribution for the very late stage. The Landau damping and growth rate are obtained through analytic solutions and kinetic Vlasov simulations.Since in a fully kinetic laser-plasma simulation,one cannot distinguish the damping from the growth behavior,we numerically solve the Vlasov–Poisson equations to find the Landau damping under different distribution functions and compare with the growth rate of SRS obtained from the Vlasov–Maxwell simulations under the same conditions.

Generally,the Landau damping prevents SRS from growing, and thus reverse trends of Landau damping and growth rate are observed all over the simulations regardless of which plasma distribution function it is, and in agreements with our theoretical predictions. For specific distribution functions,we obtain the properties of Landau damping or growth rate on their determining quantities. For example, Landau damping decreases when increasing the width of plateau, showing the enhancement of SRS as particle trapping becomes severe.The Landau damping in a bi-Maxwellian distribution function is more complicated, which depends on the choice of hotelectron temperature and hot-electron fraction.It shows a constantly increasing of Landau damping when the hot-electron fraction increases and a maximum damping existing at an optimal hot-electron temperature. In addition, we also study the effect of collisional damping on the whole damping and growth rate.

This paper is organized as follows. In Section 2,we give the theoretical derivations of Landau dampings and growth rates under three different distribution functions and the basis of our Vlasov simulations. Then we illustrate how to obtain the simulated Landau damping and growth rates in Section 3. In Section 4,the analytic Landau damping is compared with the simulation results from electrostatic Vlasov simulation,and Section 5 shows the numerical studies of the relationship between Landau damping and Raman growth rate under different distribution functions. Effects of collisional damping on the whole damping and growth rate are discussed in Section 6. Lastly,conclusions are given in Section 7.

2. Theoretical and numerical basis

2.1. Landau damping

When a Langmuir wave propagates in the collisionless plasma, particles with velocity close to the phase velocity of Langmuir wave will be resonant with the wave. Those with velocities higher than the phase velocity give excess energy to the wave, while those with velocities lower than the phase velocity gain energy from the wave. Therefore, if more resonant particles have velocities lower than the phase velocity,the total energy of the wave will decrease, which is the so-called Landau damping. Landau damping can be analyzed using the linearized Vlasov–Poisson theory. According to the standard procedure,[44]the dispersion relation of a electrostatic wave in a Vlasov–Poisson plasma is

whereDRandDIare the real and imaginary parts ofD(ω,k),andωRis the solution ofDR(ωR,k)=0. This shows that Landau damping is related to the derivative of the velocity distribution function. Therefore, we can substitute different distribution functions into the above formula to get their Landau dampings.

The most common velocity distribution is the Maxwellian distribution, which is seen in the equilibrium plasma. Its distribution function is presented in Eq. (3). Substituting it into Eqs.(1)and(2), the Landau damping under Maxwellian distribution is given by

2.2. Raman growth rate

The process of SRS satisfies the three-wave coupling equations. As is well-known, the kinetic dispersion relation of SRS is obtained by solving the linearized three-wave coupling equations in the kinetic regime,[4,10]

水合物的生成速率R(Rate)表示反应釜内甲烷水合物生成的快慢程度，可以用单位时间内甲烷的消耗量表征，见式(2)。

is the undamped growth rate under the Maxwellianian velocity distribution.

Equation (10) shows that the Raman growth rate is anticorrelated with the magnitude of Landau damping. Moreover,we can substitute the Landau dampings of different distribution functions into the formula to obtain the approximate Raman growth rates.

2.3. Vlasov solver

The simulations are performed through a Vlasov code.Considering a one-dimensional case and assuming laser propagates along thexdirection, the following equations can be used to describe the kinetic interactions between laser and plasma. They are the Vlasov equation, Maxwell’s equation,Poisson equation and momentum equation,

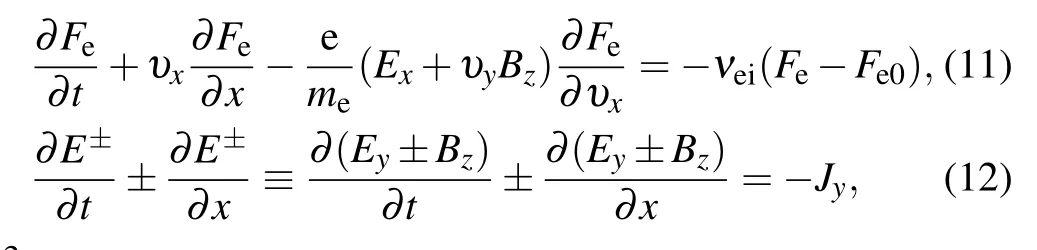
Equation(11)withBz=0 and Eq.(13)form our numerical basis of studying the Landau damping,and Eqs.(11),(12),and(14)constitute the basic equations of SRS.Also,note that although collisional damping is included in the solver (right hand side (RHS) of Eq. (11)), we neglect it during most of the time to study the non-collisional cases. In Section 6, we include this term to discuss the growth and damping with collisional effect under consideration.

3. Data processing

Note that in a fully kinetic laser-plasma simulation, one cannot distinguish the damping from the growth behavior.Therefore, two types of Vlasov simulations are implemented to study the relationship between the Landau damping of Langmuir wave and the Raman growth under various distributions. A Vlasov–Maxwell or electromagnetic Vlasov code is used to measure the growth rate of SRS extracted from the reflectivity,and a Vlasov–Poisson or electrostatic Vlasov code is used to obtain the Landau damping of Langmuir wave under the same condition of electromagnetic simulation. Here the same condition means that the Langmuir wave exited by SRS is the right wave in electrostatic Vlasov simulation, sokλDof the Langmuir waves in both simulations must keep the same. There are some fixed parameters in our electromagnetic Vlasov code. The number of total space grids isNx=6000,and L=95.5λpumpis the scale of plasma with the wave length of pump laserλpump=351 nm. The space grids of speed isNυ=256 and the maximum speed of electronυmax=0.8c,step size of time is dt=0.1ω0-1and the total length of time isNt=100000dt.

Figure 1 shows typical data from our electrostatic and electromagnetic Vlasov simulations. The Landau damping is measured from the slope of the initially decreasing logarithm of the electrostatic field as shown in Fig. 1(a). Similarly, we take a logarithm of the SRS reflectivity and measure the slope of its linear part as shown in Fig. 1(b). Since the reflectivity represents field energy which is the square of the amplitude,the amplitude growth rate is half the slope of logarithm of the reflectivity. Both of the damping and growth rates are measured in the linear stage. In addition, we have also evaluated the average reflectivity through averaging the linear part of reflectivity in Fig.1(b).

Fig. 1. (a) Plot of logarithmic electrostatic field with bi-Maxwellian distribution at υce =1, kλD =0.2911, Th/Tc =5 and f =0.06. (b)Plot of logarithmic SRS reflectivity with Ipump =2.5×1015 W/cm2,Tc =2.5 keV, ne =0.12nc, kλD =0.2911, Th/Tc =5, and f =0.06.The growth rate is measured from the slope of the red line.

4. Verification of analytic Landau damping rate through Vlasov simulation

The comparison of analytic Landau damping and simulated results are shown in Fig.2. Figure 2(a)shows the images of the Maxwellian distribution, flattened distribution, and bi-Maxwellian distribution evaluated from the Eqs.(3), (5), and(7).Compared with the Maxwellian distribution,the other two distributions have a large fraction of electrons with higher velocities.

Figure 2(b) demonstrates the dependence of Landau damping onkλDunder the Maxwellian distribution. The subscript n, t, and s represent the Landau damping obtained from numerically solving the dispersion relation by using the Hilbert transform (HT) and fast Fourier transform (FFT),[56]analytic formula, and Vlasov simulations, respectively. As is seen, three curves match and show that the Landau damping increases withkλD. The numerical solution is close to the simulated solution, but the theoretical value is slightly higher since the analytic formula(Eq.(4))is not accurate forkλD≿0.3.

Figure 2(d) presents the Landau damping under the bi-Maxwellian distribution varying with differentkλD. The trend that Landau damping increases zigzag is the same as the three curves, while with the increase ofkλD, the gap between the theoretical curve and the other two curves becomes larger since the parameter 12(kλD)2B2now exceeds the limit of being a small parameter.[40]

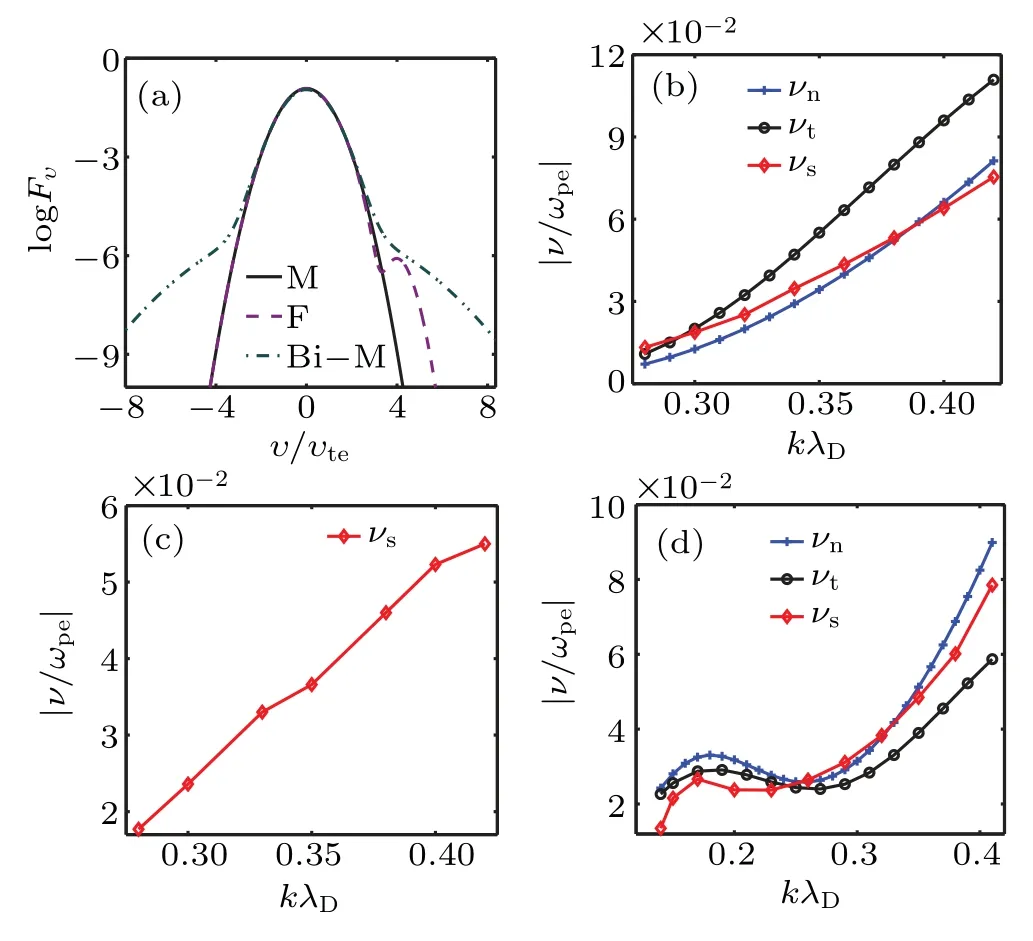
Fig.2. (a)Velocity distributions. M means Maxwellian velocity distribution. F means flattened distribution with υp =3.3411υte, Δυ =υte,and Bi-M means bi-Maxwellian distribution with f =0.05,Th/Tc=10.(b)Landau damping under Maxwellian velocity distribution,where νn,νt, and νs represent the numerical solution, theoretical solution, and simulated solution, respectively. (c) Landau damping under flattened distribution with Δυ =υte. (d) Landau damping under bi-Maxwellian velocity distribution with f =0.05,Th/Tc=10.

5. Relationship between Raman growth and Landau damping

5.1. Maxwellian distribution

Both Landau damping and Raman growth in a Maxwellian distribution have been well studied, and here we evaluate these quantities to compare with other distributions.Figure 3 is a plot of analytic and simulated Raman growth rate, obtained from Eq. (10) and the electromagnetic Vlasov code, respectively. Here, the laser intensity isIpump=2.5×1015W/cm2, wavelength is 351 nm, and plasma density isne=0.12nc. In order to show the dependence of growth rate onkλD, we change the electron temperatureTefrom 1.2 keV to 5.3 keV.It is observed that two curves match very well and the growth rate decreases withkλD. This is consistent with Eq. (10) such that the growth rate is reverse to the trend of Landau damping. It also verifies the mitigation effect of Landau damping on the Raman growth.

Fig. 3. Growth rate: γt means theoretical growth rate, γs means simulated growth rate. The parameters are Ipump = 2.5×1015 W/cm2,ne=0.12nc,and Te,from 1.2 keV to 5.3 keV.

5.2. Flattened distribution

For the flattened distribution,we change the width of the plateau to see how the plateau width affects SRS and to reveal the effect of particle trapping. The Landau damping in Fig.4(a)is obtained using the electrostatic Vlasov code. Figures 4(b) and 4(c) show the dependences of Raman growth rate and average reflectivity, respectively, on the width of the plateau using the electromagnetic Vlasov code.

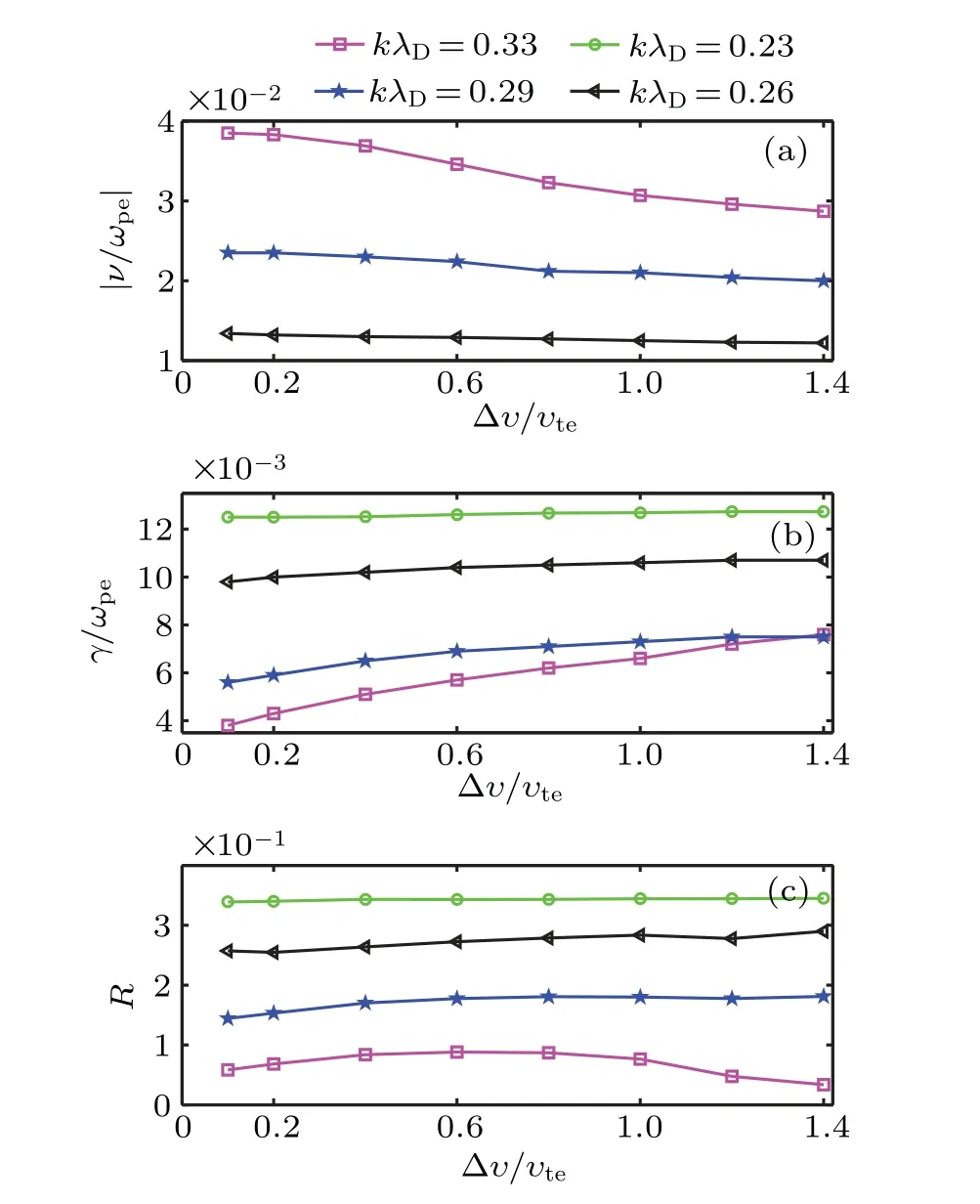
Fig. 4. (a) The Landau damping, (b) Raman growth rate, and (c)average reflectivity. The electromagnetic parameters used here are Ipump=2.5×1015 W/cm2 and Te=2.5 keV.The densities of the electron are 0.1nc, 0.12nc, 0.14nc and 0.16nc to have kλD =0.33, 0.29,0.26,and 0.23,respectively.

As the plateau width increases from 0.1υteto 1.4υte, the Landau damping decreases, leading to the increasing growth rate and average reflectivity. The increase of the plateau width essentially comes from the increase of the resonant particles whose velocities are greater than the phase velocity,therefore Landau damping decreases and,according to Eq.(10),the Raman growth increases.WhenkλD≾0.26,the Landau damping is too small to measure and is therefore not given here. At the same time, it is observed that the average reflectivity and the growth rate at smallkλDdo not change much because Landau damping at smallkλDhas no significant influence. When we compare these curves with differentkλD, it is shown that in the largekλDregime, the Raman growth is more sensitive to the plateau width, and the trends ofkλDis consistent with Fig.2(c).

In the cases ofkλD＞0.29 and Δυ＞0.8υtewith fixedIpumpandTe,we find a strange phenomenon: as the growth rate increases with the width of plateau, the average reflectivity decreases reversely. We present the evolutions of two reflectivities in Fig. 5, where (a)kλD=0.33, Δυ=0.8υte, and (b)kλD=0.33, Δυ=1.4υte. Although growth rate in (b) is indeed higher, it saturates quickly, while the growth in (a) suffers from two-stage growth and it finally has a higher average reflectivities. The behavior reminds us that distribution with larger plateau width would excite new eigenmodes in plasma,[9,12]and can detune the SRS,[9]which may attribute to this quick saturation. The discussion proves the fact that particle trapping can enhance the level SRS,while opposite effects tranquilizing the SRS could set in when the trapping width is large enough.

Fig. 5. Plot of SRS reflectivity with (a) Δυ =0.8υte, and (b) Δυ =1.4υte. The parameters used here are Ipump =2.5×1015W/cm2, Tc =2.5 keV,ne=0.1nc and kλD=0.33.

5.3. Bi-Maxwellian distribution

Next,the effect of bi-Maxwellian distribution on the Raman growth is studied. In Fig. 6(a), the bi-Maxwellian distributions of different hot-to-cold electron temperature ratios are plotted with a fixed hot-electron fraction,f=0.06,and it is observed that the fraction of resonant particles with higher velocity increases with this ratio,but the cold bulk is not sensitive to the quantity. In Fig. 6(b), distributions of different hot-electron fractions are drawn with a fixed hot-to-cold electron temperature ratio,Th/Tc=10,and the fraction of resonant particles with higher velocity increases with hot-electron fraction.

First, we show the Landau damping and Raman growth with different hot-to-cold electron temperature ratios. Figures 7(a), 7(c), and 7(e) show the dependences of Landau damping, Raman growth rate, and average reflectivity onTh/Tc.The three curves are plotted with differentkλDobtained by changingneat a fixedf=0.06.Figures 7(b),7(d),and 7(f)show the same contents and plot three curves with differentfat a fixedkλD=0.2911. In our Vlasov–Maxwell simulations,Ipump=2.5×1015W/cm2andTc=2.5 keV. Different electron densities are used to changekλDin Figs.7(c)and 7(e).

Fig. 6. (a) Bi-Maxwellian distributions of different Th/Tc and a fixed f =0.06. (b) Bi-Maxwellian distributions of different f and a fixed Th/Tc=10.

These curves have similar peak shapes where Landau damping increases rapidly and then decreases slowly with the hot-to-cold electron temperature ratio. Correspondingly, the Raman growth rate and average reflectivity are reverse to the trend of Landau damping.We can also observe that the turning point of the Landau damping and Raman growth rate slightly changes withkλDandfnearTh/Tc≈7. The critical point that makes growth rate or damping reach extreme value can be captured by the analytic formula of Landau damping. Figure 8 shows the derivative of Eq.(8)with different(a)kλDand(b)f. As is shown,the turning point(diff(|ν/ωpe|)=0)slightly decreases withkλD,and is a constant when changingf,which agree with our simulation results. The value of turning point is slightly smaller than the simulated result maybe due to the inaccuracy between theory and simulation. Since there is a negative correlation between the Landau damping and Raman growth rate,this shows that,when hot-electron temperature is about 7 times of the initial temperature, the growth of SRS is minimum. The hot-electron temperature detected by experiments is about 15 keV to 100 keV,[58]which is within the range our discussion, andThwith maximum damping is about 17.5 keV(Tc=2.5 keV),which could be a possible hotelectron temperature in the real experiments.

Second, we discuss the relationship between Landau damping and growth rate with different hot-electron fractions. Figures 9(a), 9(c), and 9(f) show the dependences of Landau damping,Raman growth rate,and average reflectivity onf,with a fixedTh/Tc=10,while Figs.9(b),9(d),and 9(f)show the corresponding contents with a fixedkλD=0.2911.The electromagnetic parameters used here areIpump=2.5×1015W/cm2andne=0.12nc. We obtain differentkλDby changing the electron temperature in Figs.9(c)and 9(e).

Fig.7. The Landau damping[(a),(b)],growth rate[(c),(d)],and average reflectivity[(e),(f)]as a function of Th/Tc. We use Ipump=2.5×1015 W/cm2 and Tc=2.5 keV in electromagnetic simulations. In(c)and(e), f =0.06 is a constant. In(d)and(f),we change f,but keep a fixed kλD=0.2911.

For the general trend,the Landau damping increases with the hot-electron fraction. The growth rate and average reflectivity have the same trend, which decreases with the hotelectron fraction. It can be seen from Figs. 9(c)–9(f) that growth rates and average reflectivities gradually approach to small values with increasing the hot-electron fraction, which indicates that large fraction of the hot electrons is good for mitigation of SRS.

Fig.8. Derivative of Eq.(10)for different(a)kλD and(b) f.

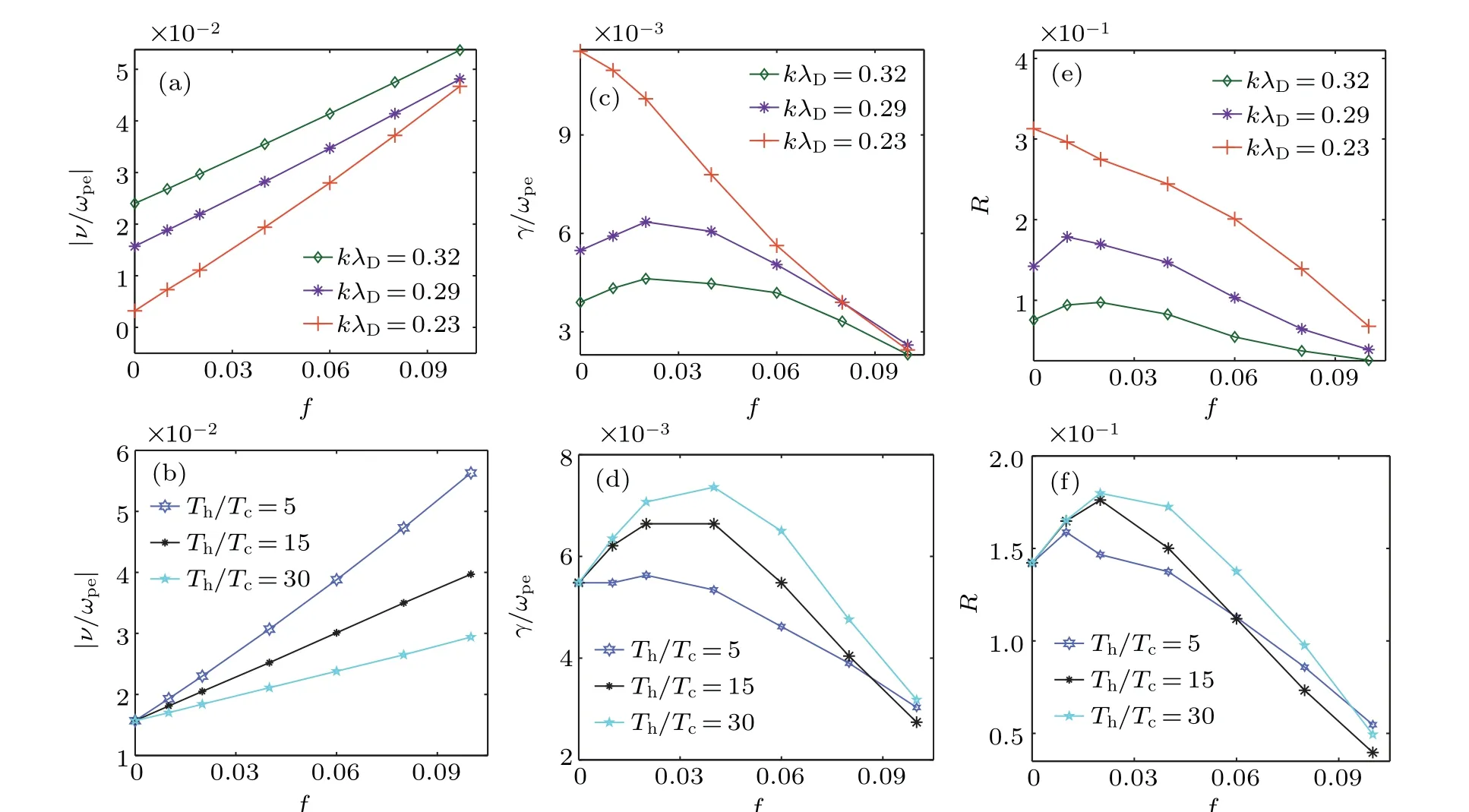
Fig.9. The Landau damping[(a),(b)],growth rate[(c),(d)],average reflectivity[(e),(f)]as a function of f. We use Ipump=2.5×1015 W/cm2 and ne=0.12nc in electromagnetic simulations. Th/Tc=10 is a constant in(c)and(e). In(d)and(f),we change Th/Tc,but keep a fixed kλD=0.2911 with Tc=2.5 keV.

6. Comparison between collisional and noncollisional cases

So far the simulations above are non-collisional, since collisional damping under these parameters is relatively small.As is well known, the collision damping rate depends on the electron temperature, density, as well as the ion charge state,some studies have found that the effect of the collisional damping is important to SRS at particular parameters.[43,47,48]Therefore, here we turn on the collisional term on the righhand side of Eq.(11)to see if it is important. The results with and without collisional damping are compared in this section.Table 1 lists the dampings and growth rates under three different distribution functions whenTe=2.5 keV,Z=1 andne=0.12nc. Here,νLCandγLCrepresent the damping and growth rates with collisional damping and Landau damping,whileνandγare the non-collisional ones. From the data,we know that under such parameters, the electron-ion collisional damping is on the order of 10-4,which is so small compared with the non-collisional damping and growth rate.

Table 1. Comparison of damping and growth rate under different distribution functions with or without collision. Ipump = 2.5×1015 W/cm2,Te =2.5 keV, Z =1, ne =0.12nc and lnΛ=9.88 in electromagnetic simulations, kλD=0.2911 in electrostatic simulations. Δυ =0.6υte in flattened distribution,and for bi-Maxwellian distribution Th/Tc=15 and f =0.0.

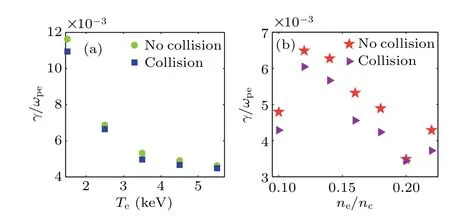
Fig. 10. Growth rate of SRS with intensity of Ipump = 2.5×1015 W/cm2, Z = 1 and wavelength of 0.351 μm. (a) The change of growth rate with temperature under the flattened distribution of Δυ=0.6υte.(b)The change of the growth rate with the electron density under the bi-Maxwellian distribution of f =0.06,Th/Tc=30.

To further illustrate the effects of collisional damping,we change the collision-related quantities, electron temperature and density, and keep the ion charge state beingZ=1. Here only the growth rates of SRS are plotted. Figure 10(a)shows the growth rate with and without collisional damping under the flattened distribution as a function of electron temperature.As temperature goes up, the growth rate decreases due to the increase ofkλDas presented in Fig.2(c). Since the collisional damping is large when electron temperature is small,large decline in the growth rate is observed. Figure 10(b) shows the dependence of growth rate on the electron density under the bi-Maxwellian distribution. The trend of growth rate is precisely reversed to the trend of Landau damping shown in Fig. 2(d)(largenemeans smallkλD). When increasing the electron density, we observe a slightly greater impact on the growth rate due to the increasing collisional damping. Overall, this analysis show that,under our parameters,collisional damping is only responsible for a slight modification on the results.

7. Conclusions

In summary, the Vlasov simulation results of Landau damping and Raman growth rate well match with the theory.It is revealed that the distribution function has a great influence on Landau damping,and thus on SRS.The growth rate is basically consistent with the trend of average reflectivity,while the Landau damping is roughly reverse to that trend. This means that we can reduce SRS by increasing the Landau damping.The detailed analyses show us the behavior of Landau dampings on different quantities such as the width of plateau and hot electrons. It gives us not only a deeper understanding of SRS in the whole stage of laser-plasma interaction,but also a possible way to mitigate SRS through manipulating these quantities to a high Landau damping regime.

Acknowledgements

This work was supported by the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No.XDA25050700),the National Natural Science Foundation of China(Grant Nos.11805062,11875091 and 11975059),the Science Challenge Project (Grant No. TZ2016005), and the Natural Science Foundation of Hunan Province,China(Grant No.2020JJ5029).