Experimental realization of quantum controlled teleportation of arbitrary two-qubit state via a five-qubit entangled state

Xiao-Fang Liu(刘晓芳), Dong-Fen Li(李冬芬), Yun-Dan Zheng(郑云丹), Xiao-Long Yang(杨小龙),Jie Zhou(周杰), Yu-Qiao Tan(谭玉乔), and Ming-Zhe Liu(刘明哲)

School of Computer and Network Security,Chengdu University of Technology,Chengdu 610059,China

Keywords: IBM quantum experience,controlled quantum teleportation,fidelity,quantum state tomography

1. Introduction

In quantum mechanics,the incredible quantum entanglement effect occurs when particles interact with each other.Quantum communication is also because of the quantum entanglement effect,and the communication process can be more stable and secure when the communicating parties carry out information transmission,which is also the difference between quantum communication and classical communication. The quantum entanglement effect can make the quantum communication process more stable, so the quantum entanglement is widely used in quantum communication, such as quantum key distribution,[1–3]quantum dense coding,[4,5]quantum teleportation,[6–8]and so on.

Since Bennet[9]proposed the concept of quantum teleportation (QT) in 1993, the quantum teleportation has been extensively studied, thus quite a lot of improved teleportation schemes have been proposed, such as quantum controlled teleportation(QCT),[10–14]quantum information splitting (QIS),[15,16]bidirectional quantum controlled teleportation (BQCT),[17,18]and hierarchical quantum teleportation(HQT),[19]etc.The most significant difference between the quantum controlled teleportation and the quantum teleportation lies in the fact that the former has a legitimate supervisor,and the communication process can only achieve the transmission of information between the two communicating parties under the supervisor’s consent. In 1998, Karlsson and Bourennane[20]first proposed the concept of quantum controlled teleportation.in which the GHZ state is used as a quantum channel to realize the transmission of quantum state,and the receiver can reconstruct Alice’s quantum state only with the permission of the overseer. In 2008, Chenet al.[10]proposed a QCT of an unknown two-qubit entangled state by using a three-qubit W state as a quantum channel,and an appropriate quantum circuit was constructed to realize the teleportation process. In 2015, Chenet al.[11]improved the scheme of quantum controlled teleportation proposed by Liet al.,[12]they constructed a novel three-qubit partially entangled state as a quantum channel to realize the QCT.The scheme of QCT is evaluated from three aspects: fidelity, success probability,and the capability of the controller. The detailed calculation and simulation results show that the three-qubit partially entangled state can be used as a quantum channel to realize the QCT of any qubit. In 2017,Zanget al.[13]proposed a scheme by using a six-qubit cluster state as quantum channel to realize two different QCT schemes,namely,three-party and fourparty communication, and the schemes were finally found by comparison to increase the security of the information transmission with the increase of the controlling party,but the operation of reconstructing quantum state is more complicated. In 2018, Zhouet al.[14]proposed that the combination of twoqubit cluster state and three-qubit cluster state is used as a quantum channel to achieve an arbitrary two-qubit QCT, and the scheme is used to calculate the success probability of the communication process with the classical amount of information. In 2020, Liet al.[21]proposed a QCT scheme by using a seven-qubit entangled state as quantum channel to realize a Bell state,and they used decoy photons to demonstrate that the scheme has high security.

Since IBM quantum experience (IBM QE)[22–25]was opened to the public free of charge in 2016, users have been able to use the interactive graphical interface provided by the platform to design quantum circuits for IBM QE experiments,and choose real quantum computer or quantum simulator to test and run quantum circuits. In 2020, Baishyaet al.[25]used the IBM QE platform to test and verify his teleportation scheme of arbitrary two-qubit states through using the fourqubit cluster state as the quantum channel. In this paper, we also use the IBM QE platform, which is freely available to users,to verify the operation process of our proposed scheme in which a five-qubit entangled state is used as a quantum channel to achieve arbitrary two-qubit QCT.Up to now,there have been many theoretical schemes about quantum communication that can be implemented on IBM QE, such as quantum algorithm,[26]quantum error correction,[27]quantum key distribution protocol,[28]etc.

The rest of this paper is organized as follows. In Section 2,the scheme of QCT of arbitrary two-qubit states is discussed both theoretically and experimentally. In Section 3,the experimental data are collected and the transmitted quantum states are analyzed through quantum state tomography.In Section 4,a sequence of photon states is introduced to analyze the security of the scheme. Finally,in Section 5 some conclusions are drawn from the present findings of this study.

2. Theoretical and experimental study of quantum controlled teleportation of arbitrary twoqubit state

The process of quantum controlled teleportation of arbitrary two-qubit states are studied by using a five-qubit entangled state as the quantum channel. Assuming that there are three valid participants in the scheme: Alice, Bob, and Charlie: Alice is the sender,Bob is the receiver,and Charlie is the supervisor, the three communicators take the following specific steps in this scheme to achieve arbitrary two-qubit transmission.

Step 1 Alice,Bob,and Charlie share a five-qubit entangled state as the quantum channel before performing the transmission of the quantum state,and the five-qubit entangled state is defined as follows:where|a|2+|b|2+|c|2+|d|2=1.

Fig.1. Quantum circuit generating five-qubit entangled state.

The whole system is written as

where qubitsa,b, 1, and 2 belong to Alice, qubits 4 and 5 belong to Bob,qubit 3 belongs to Charlie.

Step 3 Alice performs Bell state measurements on its qubit pairs(a,1)(b,2),respectively,and the remaining qubits 3,4,and 5 will collapse into 16 equal possible collapse states after the measurements,then Alice sends its measurement results to Bob and Charlie, and if Charlie allows Bob to reconstruct the initial state, the single qubit measurement will be perform with the basis of{|0〉,|1〉}on qubit 3 and sends the results to Bob,at which point Bob can reconstruct arbitrary twoqubit state by combining the measurement results of Alice and Charlie. The Alice measurements, Bob and Charlie collapse states,Charlie measurements,Bob collapse states,and unitary operations performed by Bob are shown in Appendix A.

The Bell state measurements performed by Alice can be written as

Then Alice sends the measurement results to Bob and Charlie.When Bob and Charlie receive the Alice’s measurement result and Charlie allows Bob to reconstruct the arbitrary two-qubit state|ψ〉ab, then Charlie takes the single qubit measurement with the basis of{|0〉,|1〉}on qubit 3 and sends the measurement results to Bob. Bob can reconstruct arbitrary two-qubit states if Charlie’s measurement result is|0〉5or|1〉5by performing the unitary operationσx ⊗σxon qubits 4 and 5. The complete quantum circuit of the schematic diagram is shown in Fig.2.

Fig.2. Quantum circuit of quantum controlled teleportation of arbitrary two-qubit state.

Figure 2 shows the quantum circuit of an arbitrary twoqubit controlled quantum teleportation run on IBM QE with IBM qsam simulator. As shown in Fig. 2, part (a), in box I,shows the quantum circuit of an arbitrary two-qubit state generated by twoUgates (θ=π/2,φ=0,λ=0), and the box II is the same as that in Fig.1,which shows the quantum circuit of five-qubit entangled state generated with X gates, H gates,and CNOT gates. Part(b)is the Bell state measurement performed by Alice on its qubit pairs(a,1)and(b,2),respectively. Part(c)is the single qubit measurement performed on qubit 3 after Charlie has agreed to help Bob to reconstruct an arbitrary two-qubit state.

The measurement results of this circuit diagram run on IBM qsam simulator with the number of shots set to 1024 and 8192 respectively are shown in Fig.3.

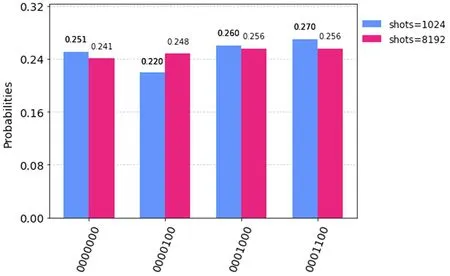
Fig.3. Histogram of experimental results of quantum controlled teleportation of arbitrary two-qubit state by using five-qubit entangled state.

3. Quantum state tomography

In this section, we adopt quantum state tomography,[29–32]a method which describes in detail the accuracy of the quantum state transfer process. Usually, the quantum state tomography is analyzed by using theoretical density matrix and experimental density matrix.

Firstly,the theoretical density matrix of the quantum state is expressed as follows:

We use the fidelity to calculate the degree of overlap between the theoretical and experimental transmitted two-qubit state density matrices, indicating that the greater the fidelity,the higher the degree of overlap between the theoretical and experimental density matrices is, and that the smaller the fidelity,the lower the degree of overlap between the theoretical and experimental density matrices is,and the fidelity equation is given as follows:

Fig. 4. Real and imaginary parts of [(a) and ((b)] theoretical density matrix and [(c) and (d)] experimental density matrix of the two-qubit state transmitted by this scheme. The above experiments were performed on the IBM qsam simulator.

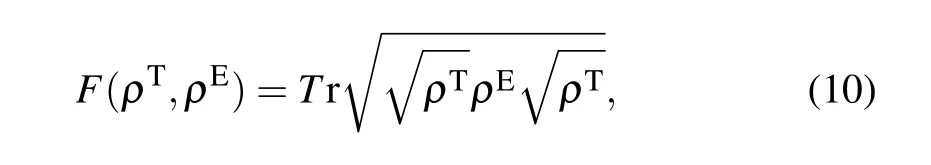
whereρTrepresents the theoretical density matrix andρEdenotes the experimental density matrix.

By calculations, we can conclude that the fidelity of this scheme is 0.4925.

4. Security analysis

The security of the quantum controlled teleportation carried out in this scheme is analyzed in this section. In the process of preparing the five-qubit entangled state, Alice was asked to prepare a sequence of photon states{|H〉,|V〉,|D〉,|A〉,|R〉,|L〉}, for eavesdropping detection, in which three pairs of states are orthogonal to each other, and we know that the inner product of these three pairs of orthogonal states is 0, such as〈H|V〉= 0. We will also use the properties of these three pairs of orthogonal states to examine whether the information has eavesdropped during transmission. When Alice sends the quantum state, the photon state from the prepared sequence is randomly inserted into the quantum state to be sent, and the specific information of the insertion is known only to Alice. When Bob receives the quantum state, Alice informs Bob of the specific information of the photon state insertion and the method of verifying the photon state. Next, we will use this method to analyze three attacks from intercept–replace–resend, intercept–measure–resend,and entanglement–measure–resend.

4.1. Intercept–replace–resend attack

Suppose that in this scheme,there is an eavesdropper Eve(or dishonest Charlie) in the process communication, when Alice transmits the information to Bob,Eve intercepts the information sent by Alice in the channel and sends the quantum state prepared in advance to Bob,since Alice has inserted the prepared photon state randomly into the quantum state before sending the information, Therefore, when Bob receives the quantum state from Charlie,Alice informs Bob of how to check the photon state,and then Bob applies this information to the inner product with the corresponding photon state. If Alice tells that the photon states|R〉and|D〉are inserted at positionsiandjof the quantum state, then Bob simply applies the photon states|L〉and|A〉informed by Alice to innerproduct with taking out the corresponding photon states|R〉and|D〉,respectively.Since Charlie does not know the specific information of the photon states randomly inserted by Alice in advance, so Bob cannot find the corresponding photon states|R〉and|D〉at positionsiandjwhen he wants to perform the inner product operation,so that Bob makes an error during the inner product. Eve’s eavesdropping will be detected so that he cannot get any information about the quantum state.

4.2. Intercept–measure–resend attack

In this scheme,an eavesdropper named Eve(or dishonest Charlie) is supposed to be in the process of communication.In the process of Alice transmitting information to Bob, the eavesdropper intercepts Alice’s information,trying to measure the quantum state to get information about the quantum state sent by Alice. Since Alice has randomly inserted the photon state into the quantum state before sending the information,once the eavesdropper Eve measures the quantum state sent by Alice to Bob,it will change the original state of the photon state. Therefore, when Bob receives the quantum state sent by Eve, checking the quantum state with the detection information sent by Alice will not be successful, so Eve’s eavesdropping will be detected, and the eavesdropping is ended in failure.

4.3. Entangle–measure–resend attack

Alice randomly inserts the photon states into the quantum state before sending it, so when Eve entangles with the quantum state sent by Alice, some of the qubits will also be entangled to the photon state. When Eve performs the single qubit measurement, the entangled photon state will be affected. When Bob performs eavesdropping detection on the received quantum state,it will detect the presence of an eavesdropper eavesdropping,so Eve fails to eavesdrop. It will not be able to obtain any useful information.

5. Conclusions

In this paper, we proposed a scheme to realize the quantum controlled teleportation of an arbitrary two-qubit state by using a five-qubit entangled state as the quantum channel. In the scheme, we first discuss the theoretical process of quantum controlled teleportation of arbitrary two-qubit in detail,then design a proper quantum circuit on IBM QE, and run the circuit with the 5-qubit IBM qsam simulator, at the same time, the histogram of experimental results and the results of quantum state tomography show that we successfully demonstrate our program on IBM QE. We calculate the fidelity of this scheme by using the theoretical and experimental density matrices, and the fidelity can reach nearly 50%. Finally, a sequence of photon states is introduced to ensure the communication security of the scheme. In this paper, the theoretical and experimental results of teleportation are obtained, which provides a reference for other quantum communication experiments in the future. Quantum communication and quantum computing are both important branches of quantum information,and the combination will significantly promote the development of quantum informatics.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 61802033 and 62172060) and the Key Research and Development Project of Sichuan Provincial Science and Technology Plan, China (Grant No.2020YFS0445).

Appendix A

Table A1. Alice measurement, Bob and Charlie collapse states, Charlie measurement, Bob collapse states, and unitary operations performed by Bob are listed.