High-resolution boosted reconstruction of γ-ray spectra∗
LI Lei(李磊),TUO Xian-Guo(庹先国),LIU Ming-Zhe(刘明哲),and WANG Jun(王俊)
1State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology,Chengdu 610059,China
2Nuclear Technology and Automation Engineering Institute, Chengdu University of Technology,Chengdu 610059,China
3Key Subject Laboratory of National Defense for Radioactive Waste and Environmental Security, Southwest University of Science and Technology,Mianyang 621010,China
High-resolution boosted reconstruction of γ-ray spectra∗
LI Lei(李磊),1,2TUO Xian-Guo(庹先国),1,3,†LIU Ming-Zhe(刘明哲),1,2and WANG Jun(王俊)1,2
1State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology,Chengdu 610059,China
2Nuclear Technology and Automation Engineering Institute, Chengdu University of Technology,Chengdu 610059,China
3Key Subject Laboratory of National Defense for Radioactive Waste and Environmental Security, Southwest University of Science and Technology,Mianyang 621010,China
Direct demodulation method(DDM)was applied to reconstruct γ-ray spectra.Boosted Richardson-Lucy iteration was introduced into DDM.Monte Carlo method(here GEANT 4)was proposed to calibrate response function and establish response matrix.First,gauss function was regarded as total energy peak.Spectra line was simulated with nine gauss functions.And afterwards DDM was applied to reconstruct the simulated spectra line and determine peak positions and areas.Compared with original spectra,for case that peak position interval was about 1/3 full width half maximum(FWHM),the error of rebuilding peak position was 2 channels.The rest of peaks could be searched accurately.The relative errors of all peaks’area were less than 4%.Then,three key factors,including noise,background,response matrix,were discussed.Finally,DDM was applied to calibrate the field NaI gamma spectrometer.The errors of U,Th,K were less than 5%.Comprehensive studies have shown that it is feasible to reconstruct gamma-ray spectra with DDM.DDM can significantly pseudo-improve energy resolution of gamma spectrometer,effectively decompose doublets whose peak potential interval is 1/3 FHWM,and accurately search peak and calculate areas.DDM can restrain noise strongly but is greatly influenced by background.And DDM can improve the accuracy of qualitative and quantitative analysis in combination with the conventional spectrum analysis method.
Direct Demodulation Method(DDM),Monte Carlo,GEANT4,Reconstruction,Doublets
I.INTRODUCTION
Gamma energy spectrum analysis is a technique of using gamma spectrometer to measure γ-rays of radionuclides and determine directly categories and contents of particular radionuclides by processing the measured γ-ray spectra.Generally,the data processing includes smoothing,background deduction,peak searching,calculation of peak areas and energy calibration.Certainly,peak position and peak area are the key to qualitative analysis and quantitative analysis respectively.Traditional peak searching methods[1]includes IF function method,Gaussian product function method,derivative method,covariance method,and symmetrical zero area transformation method.Although they can be of high precision for strong radioactive γ-ray spectra and singlet,these peak searching methods are rough for weak radioactive γ-ray spectra and doublets.Especially for weak radioactive γ-ray spectra,IF function method,Gaussian product function method and covariance are not desirable[2], while derivative and symmetric zero area methods have limited effects.
Most of the traditional peak area methods,such as totalpeak area(TPA)method,Covell peak area method,Wasson peak area method,Sterlinski peak area method,Wasson-Sterlinski peak area method,Quittner peak area method,WS-Qpeakareamethod,andQ-Speakareamethod,requestdetermination of the peak position and border,and can be only applied for singlet only[3].
The curve fitting method performs better[4,5].Its basic principle is as follows.A mathematical model,or a function,is established to describe the shape of total energy peak and baseline,then parameters of the function are determined from the experimental data,and finally the peak area is obtained by integrating the function.In practice,however,due to complexity of detectors and detection environment,measured γ-ray spectra are often too complicated to determine the function.In other words,application of the curve fitting method of peak area is extremely circumscribed.
In 1997,de-convolution[6]was proposed to process γ-ray spectra.For ill-posed problems,conventional de-convolution methods,such as maximum entropy method[7],is sensitive to the error of input data,namely,a small error can cause great oscillation.Fortunately,Tikhonovet al.studied illposed problems in 1977 on a strict mathematic basis by introducing the regularization theory and methods[8].The idea is to transform ill-conditioned problems into well-posed problems,so as to ensure the solution acceptable and stable enough.Regularization falls into three categories generally:the least squares,smoothing methods,and iterative. The least-squares method is vulnerable to premature and the solutions have large error[9].The degree of smoothing is not easy to control and smoothing itself has error[10].In theiterative approach,one attempts to generate successive approximations which converge to an appropriate solution.Perhaps the most significant feature of iterative method,for the unfolding application,lies in the ability to incorporate readily most of the major physical implication of the description. Also,the necessity for an explicit calculation of the inverse matrixisavoided[11].Thisisimportant,asthemostresponse matrices are ill-conditioned,and the error in the elements of the inverse matrix can be prohibitive.
There are three commonly used regularization(iteration) de-convolution methods:Gold[12],Richardson-Lucy[13], and the maximum posteriori algorithms[14].The direct demodulationmethod(DDM)[15,16]wasproposedbyLiTibei and Wu Mei.Its basic principle is to use some known physical conditions to control iterative process for solving modulation equation.The Richardson-Lucy iteration converges to the maximum likelihood solution.Compared with conventional de-convolution methods,DDM can be rarely restricted by shape of γ-ray spectra,radioactive intensity,and error of input,by taking full advantage of known information and utilizing nonlinear physical constraint conditions.DDM has succeeded in high-energy astronomy for reconstructing astrophysical images of low signal-to-noise ratio(SNR),low statistics and low-resolution[17–19].But there are rarely reports about DDM for γ-ray spectra.In this paper,we propose to utilize DDM to reconstruct γ-ray spectra.Monte Carlo simulation is performed to calibrate response functions and establish response matrix.The purpose of this study is to improve the energy resolution of gamma spectrometry,and accuracy of γ-ray spectra analysis.
II.THE DIRECT DEMODULATION METHOD
The input and output of gamma spectrometer can be regarded as a complete system.The incident radiation can be imaged as a sum ofδ-functions.So at the system output the spectrum represents a linear combination ofδ-functions with various amplitudes located at various channels function, which are blurred by the system response functions.The purposeofDDMwas toeliminatethe influenceof responsefunction to the utmost.Ideally,a complete γ-ray spectra consisting ofδ-functions can be obtained.
Let us suppose that the intensity distribution function of source isf(x).From a signal processing point of view,measurement process of spectrum can be regarded as the modulation process of spectrum of radioactive source.The measured γ-rayy(j)is the modulated result.The modulation equation can be expressed as

whereh(j,x)represents the system response function.
The matrix equation can be expressed as

whereHis system response matrix.For γ-ray spectra,His the lower triangular Toeplitz matrix:
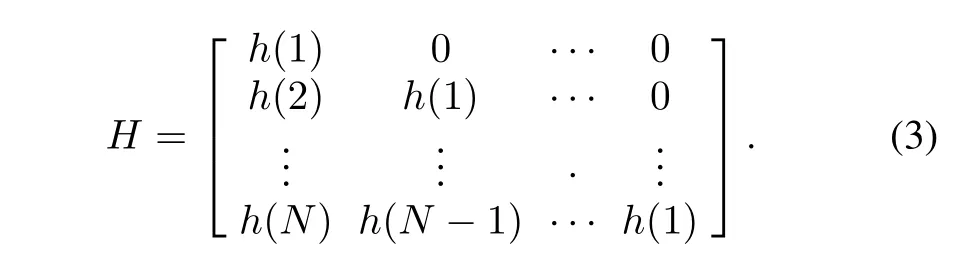
Equation(2)means that spectrum of radioactive sourceFismodulated by gammaspectrometer,and the measured spectrumYis obtained.The reconstruction process is an inverse process:demodulate the spectrumYto reconstruct spectrum of radioactive sourceF.
For gamma spectrometry,y(j)andf(x)are both nonnegativediscretepoints.Itshouldbeemphasizedthatthisisvitally important for DDM.Besides,h(j,x)is discretized in the numerical calculation.Hence the discrete form of Eq.(1)can be expressed as

whereh(k,j)is the element at thekthrow andjthcolumn of response matrixH,f(j)is thejthelement ofFandy(k)is thekthelement ofY.However,Eq.(4)is an ill-posed problem.So DDM is applied for Eq.(4).
Richardson-Lucy iteration algorithm(R-L)is based on Bayesian statistical theory.It can be expressed as
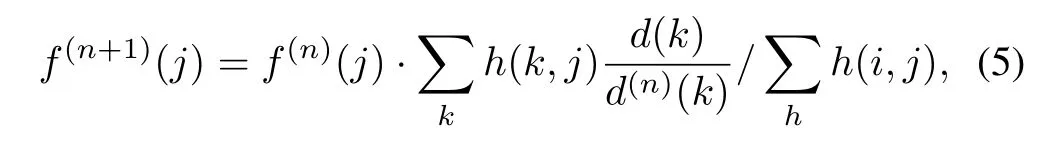
whered(n)(k)=Ph(k,j)f(n)(j).However,Eq.(5)is apt to“premature”.So an enhanced Richardson-Lucy iterative algorithm[8]is applied in this paper.
The nonlinear physical constraints,including upper limit and lower limit,can be expressed as[20]

Obviously,each element ofFis less than the upper limit. So the lower limit only needs to be considered.For γ-ray spectra,background is regarded as the lower limitb(j).
Equations(5)and(6)consist a complete representation of DDM.Referring to Ref.[8],exponential factorpwas introduced to DDM.The principles of enhanced DDM can be expressed as follows:
Step 1:forn=0,set the iterative initial valuef(0)= [1,1,···,1]T;
Step 2:setting the number of iterationsLand cycle numberR;
Step 3:initializing the cycle numberr=1;
Step 4:according to Eq.(4)to calculate and seek the solutionf(L);
Step 5:introducing parameterp,andf(0)(i)=?f(L)(i)?p,p∈(1,2),i=0,1,···,N−1;
Step 6:introducing physical constraints;
Step 7:ifr=R,then stop calculating.Otherwise,r=r+1,continue to do Step 4.
III.RESULTS AND EVALUATION
The difficulty evaluation in separation of doublets of IEC standard[21]is given in Table 1.Referring to it,the Gaussian function was used to simulate nine full-energy peaks.Their positions,heights and areas are listed in Table 2.The synthetic spectrum is shown in Fig.1(a).From Table 2,the biggest ratio in height is 10:1,and the minimum interval of peak positions is less than 1/3 FWHM.All cases except for area ratio 1:100 in Table 1 are considered.The spectral line was reconstructed by applying DDM with 1000(L=50,R=20,p=1.8),5000(L=100,R=50,p=1.8), 10000(L=200,R=50,p=1.8),and 50000(L=500,R=100,p=1.8)iterations,respectively.Then,peak areas were calculated by accumulating counts for“isolated”singlet of reconstructed spectrum.The result of 50000 iterations is shown in Fig.1(b).
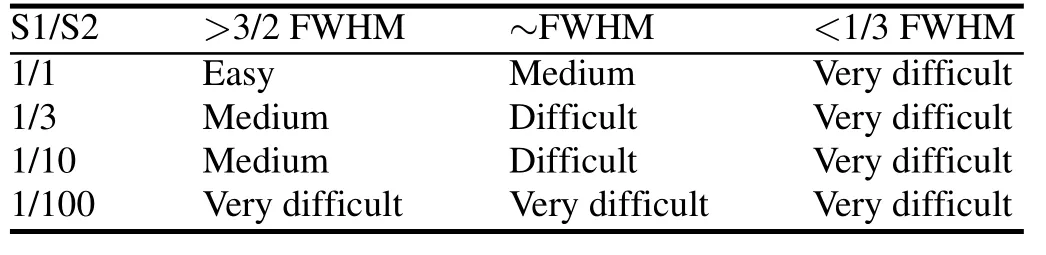
TABLE 1.Difficulty evaluation in separation of overlapped peaks of IEC standard.

TABLE 2.Difficulty evaluation in separation of overlapped peaks of IEC standard
Also,width of the reconstructed peak decreased with increasingnumberofiterations.Theoretically,acompletespectrum consisting ofδ-function(single pulse)can be obtained after a large number of iterations.And corresponding counts of pulse are peak areas.But a bigger iteration means more time and memory consumed.Thus,from the perspective of ef fi ciency,iteration is stopped when doublets are completely separated.The peak areas are not the corresponding counts of pulse,but the sum of corresponding counts of a few“isolated”points.The results show that DDM can effectively decompose the peaks overlapped by just 1/3 FWHM.It should be emphasized that this is an extremely dif fi cult task.
Table 3 lists the peak positions and areas of the DDM-reconstructed spectrum.For area ratio of 1:1 and peak position interval of about 1/3 FWHM,the error of peak position is 2 channels;while it is 1 channel for area ratio of 1:10 and peak position interval of about FWHM.The peak area error is less than 4%for all cases.This indicates that positions and areas can be precisely obtained with DDM.

Fig.1.(Color online)synthetic spectrum(a)and reconstructed spectrum using DDM algorithm after 50000 iterations(b).
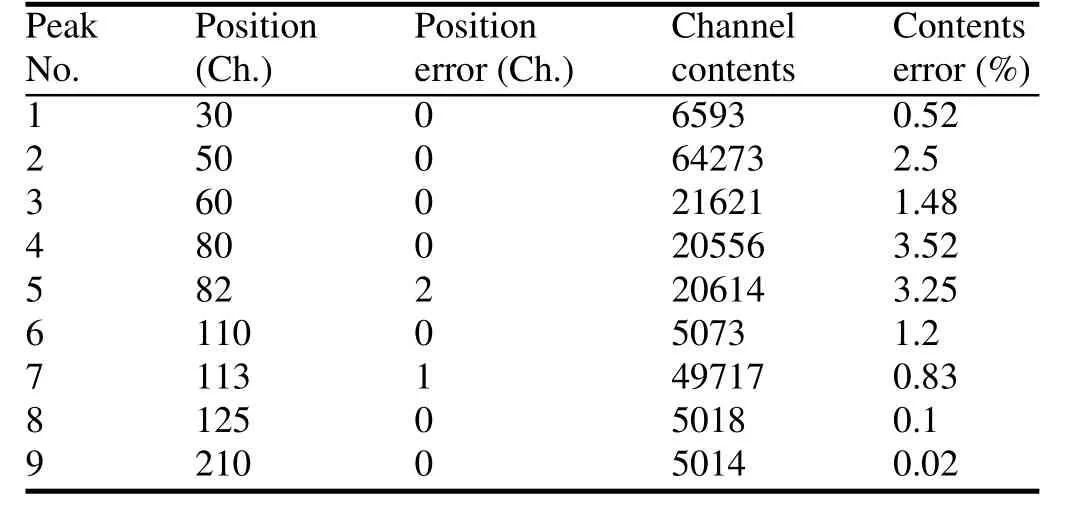
TABLE 3.Reconstructed peak positions,channel contents and their errors in the spectrum shown in Fig.2
IV.DISCUSSION
Actually,a measured γ-ray spectrum usually contains noise and background.Therefore,it is necessary to study the influence of noise and background on DDM.
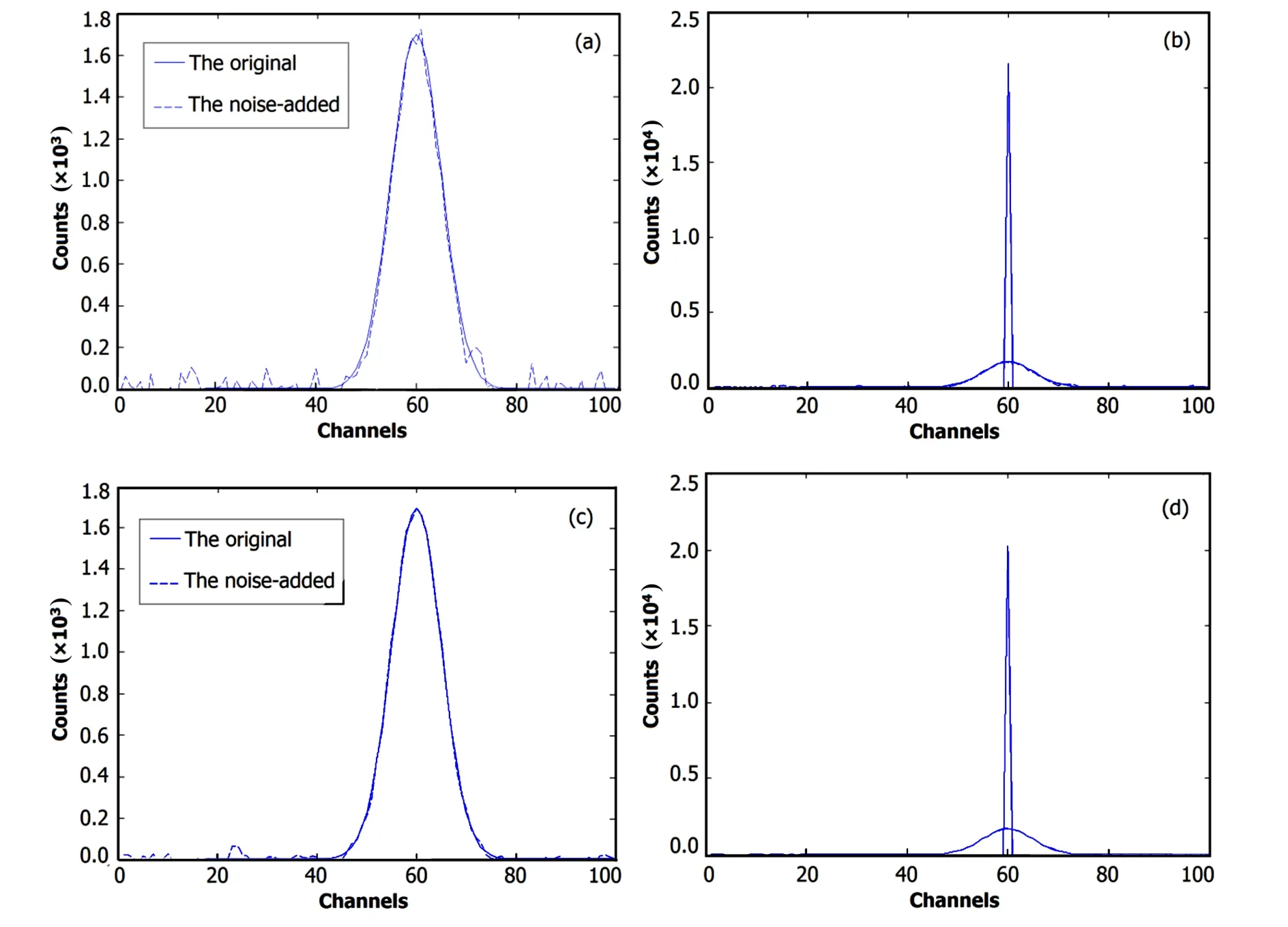
Fig.2.(Color online)A Gaussian peak and its DDM reconstructed spectrum.(a)and(b)peak with random noise and the DDM result;(c) and(d),peak with gauss noise and the DDM result.
A.Noise
A Gaussian peak is added with random(Fig.2(a))and gauss(Fig.2(c))noises,in amplitudes of 3%and 1%of the Gaussian peak height,respectively.The results are shown in Figs.2(b)and 2(d),respectively.One sees that DDM has a strong inhibitory effect on noise.Because the least-squares, smoothing methods,and iterative can solve ill-conditioned problem,and the Richardson-Lucy iteration algorithm is adopted,noises can be intangibly inhibited in the process of iteration.If the noise is not serious,a spectrum can be reconstructed without de-noising.
B.Background
A spectrum is added with straight-line,oblique-line,and step backgrounds,respectively.The DDM-reconstructed results are shown in Fig.3.The spectra were not reconstructed correctly.This indicates that background affected the accuracy of reconstructed spectra,but researches show that if the response matrix can be obtained under the same condition of background,or the background can be removed from the measuredspectrumandresponsematrixbyapplyingthesame way,the lines can be reconstructed accurately.
C.Establishment of response matrix with GEANT4
Experiments have shown that the response function of a spectrometer system is strongly dependent on energy of the incident γ-rays.Heretofore,there are no unanimous theories and empirical expressions,but we could obtain the response function experimentally.Ideally,the response functionshallbecalibratedbyusingstandardradioisotopesources to have strong single peaks distributed uniformly throughout the whole energy range.However,it is impractical to obtain so many standard sources and the γ-ray peaks cannot be in such a uniform distribution.Fortunately,Monte Carlo method can correctly simulate response function of γray spectra[22,23].Above all,distribution and energy of radioactive source can be artificially controlled.
GEANT[24]can be used for neutron,photon,electron,or coupled neutron/photon/electron transport,proton,etc.,and is capable of calculating eigenvalues for critical systems.For photons,the code accounts for incoherent and coherent scattering,possibility of fluorescent emission after photoelectric absorption,absorption in pair production with local emission of annihilation radiation,and bremsstrahlung.Above all,the photon energy regime is from 1eV to 100GeV for Rayleigh and Compton effects,down to the lowest binding energy for each element for photo-electric and ionization,and down to10eV for bremsstrahlung.GEANT4 was employed in the work.

TABLE 4.The scaling factor and net areas of the NO.104 gamma-ray spectrometer

Fig.3.(Color online)Spectra with backgrounds in(a)straight line, (b)oblique-line and(c)steps,and the reconstructed spectra.
In order to coincide with experiment,properties of the detector must be revised before simulation.241Am(0.06MeV),57Co(0.122MeV),22Na(0.51MeV),137Cs(0.661MeV),and24Na(1.38MeV,2.75MeV)were selected.The crystal dimensions were adjusted to keep spike and full-energy peak efficiency of the measured spectrum coincidence with the simulation results.Then,according to the data of energy calibration,corresponding energy per channel was chosen to simulate response function.It was adjusted according to multichannel analyzer.And the analog data of each single peak were normalized as response function of this energy.The response function needs to be converted to response matrix for its use in DDM:measurement spectrum is convolution of input data and response function.So referring to the convolution process,response function is reflexed,zero filled,and gradually shifted to get a series of two-dimensional vectors which constitute response matrix.
V.CALIBRATION OF NAI GAMMA SPECTROMETER BASED ON DDM
DDM was used to calibrate the field NaI gamma spectrometer.Generally,spectrum stripping was used.The principles of calibration can be seen in Ref.[25].IED-3000A NaI gamma spectrometer(104#)was used.The dimensions of NaI crystal were 75mm×75mm,with an energy resolution of 10.3%(661keV).The measuring time was 3600s.Substance contents of quasi-saturation model were listed in Table 4,which were measured by Analysis and Test Center of China Geological Survey.
The measured spectrum of hybrid model was shown in Fig.4(a).SNIP[26]was applied to deduct background. DDM was used to reconstruct the spectrum.The result after 50000 iterations is shown in Fig.4(b).Calibration coefficients and net peak areas of 1.46MeV(40K),1.76MeV (214Bi of U series),and 2.62MeV(208Tl of Th series)are listed in Table 4.
Table 5 shows the elemental analysis results of a γ-ray analysis standard by applying DDM and spectrum stripping method(SSM),It can be seen that the DDM results are of smaller deviations from the given value of U,Th and K,being respectively−1.02%,−4.19%and−2.41%,while the SSM results deviatedby−8.06%,10.44%and8.84%,respectively.

TABLE 5.Results of No.104 gamma-ray spectra with DDM and spectrum stripping method(SSM)
VI.CONCLUSION
Duetoresponse functionanditerativealgorithm,DDMcan be rarely restricted by shape of γ-ray spectra,radioactive intensity.Besides,DDM can significantly pseudo-improve energy resolution,precisely search peaks,calculate areas,and improve the performance of gamma spectrometer without hardware cost.It is worth mentioning that response matrix is the key of DDM.However,in practical,it is tedious and difficult to use the standard radioactive sources to establish response matrix.Hence GEANT 4 was proposed to calibrate response function.It is convenient,safe,and effective to employ Monte Carlo method to establish response matrix.
On the other hand,in theory,DDM can pseudo-improve energy resolution to infinity after a large number of iterations.But the bigger iterations,the more time and memory will be consumed.Thus,from the perspective of efficiency, we should stop iteration when doublets were completely separated.
It should be emphasized that,theoretically,DDM is not only appropriate for γ-ray spectra but also for any other spectrum as long as response matrix can be established correctly. In fact,DDM is not only just applied to NaI(Tl)detector but also to any other detector.It is time-consuming to establish response matrix and run DDM,especially for the complex spectrum.Thus,DDM is usually regarded as a means for offline analysis.In this respect,how to improve the running speed will be focused during the next study.
[1]Pang J F.Gamma-ray spectrum analysis.Xi’an(CHN):Shanxi Science and Technology Press,1993,577–608.(in Chinese)
[2]Pang J F,Zheng G F,Hou X F.Atom Energy Sci Technol,1987,21:270–279.(in Chinese)
[3]Pang J F.Gamma-ray spectrum analysis.Xi’an(CHN):Shanxi Science and Technology Press,1993,365–402.(in Chinese)
[4]Kokta L.Nucl Instrum Methods,1973,112:245–251.
[5]Li Z,Tuo X G,Shi R,et al.Nucl Sci Tech,2013,24:060206.
[6]Morhac M,Kliman J,Matousek V,et al.Nucl Instrum Meth A, 1997,401:385–408.
[7]Kong Y and Lynn K G.Nucl Instrum Meth A,1991,302:145–149.
[8]Tikhonov A N and Arsenin V Y.Solutions of Ill-posed problems.In:Fritz John,editor.Wiley,New York(USA):Winston distributed solely by Halsted Press,1977,52–80.
[9]Morh´aˇc M and Matouˇsek V.J Comput Appl Math,2011,235: 1629–1640.
[10]Scofield N E.A Technique for Unfolding Gamma-Ray Scintillation Spectrometer Pulse-Height Distributions.Naval Radiological Defense Laborator USA,USNRDL-TR-447,1960.
[11]Vetter W J.Siam Rev,1973,15:352–369.
[12]Gold R.An Iterative Unfolding Method for Response Matrices. Argonne National Laboratories,Argonne,ANL-6984,1964.
[13]Lucy L B.Astron J,1974,79:745–754.
[14]Olofsson T and Stepinski T.Ultrasonics,1999,37:423–432.
[15]Li T P and Wu M.Astrophys Space Sci,1993,206:91–102.
[16]Li T P and Wu M.Astrophys Space Sci,1994,215:213–227.
[17]Lu F J,Li T P,Sun X J,et al.Astron Astrophys Suppl,1996,115:395–400.(in Chinese)
[18]Li T P.Exp Astron,1995,6:63–69.
[19]Li T B and Wu M.Chin Astron Astr,1993,17:453–463.
[20]Shen Z J.Ph.D.Thesis,Tsinghua University,2007.(in Chinese)
[21]Ai X Y.PH.D.Thesis,Tsinghua University,2005.(in Chinese)
[22]Yue K,Liang J,Sun Z,et al.Nucl Phys Rev,2010,27:436–439.(in Chinese)
[23]Yang J B,Yang Y G,Li Y J,et al.Nucl Sci Tech,2012,23: 337–343.
[24]Agostinelli S,Allison J,Amako K,et al.Nucl Instrum Meth A, 2003,506:250–303.
[25]Liu Q C,Jia B S,Wan J.Introduction to Nuclear Science.Heilongjiang(CHN):Harbin Engineering University Press,2004, 79–81.(in Chinese)
[26]Morhac M.Nucl Instrum Meth A,2009,600:478–487.
10.13538/j.1001-8042/nst.25.050202
(Received December 31,2013;accepted in revised form May 1,2014;published online September 29,2014)
∗Supported by National Science Foundation for Distinguished Young Scholars(No.41025015),Natural Science Foundation of China(No. 41274130),Sichuan Youth Science and Technology Innovation Team(No. 2011JTD0013),and Sichuan Province Science and Technology Support Plan(No.2013FZ0022)
†Corresponding author,13982021384@163.com
 Nuclear Science and Techniques2014年5期
Nuclear Science and Techniques2014年5期
- Nuclear Science and Techniques的其它文章
- The effect of Nb additive on Te-induced stress corrosion cracking in Ni alloy:a fi rst-principles calculation∗
- Development and testing of the code for automatic generating of multi-temperature continuous-energy neutron cross section libraries∗
- Steady thermal hydraulic characteristics of nuclear steam generatorsbased on the drift flux code model∗
- A method of estimating and subtracting the hydrogen background in the natural carbon target used in the12C+12C experiment∗
- Density functional theory study of H,C and O chemisorption on UN(001)and(111)surfaces∗
- The extraction and smoothing algorithms for γ-ray spectrum of a CdZnTe detector system
