MAPS PRESERVING THE NORM OF THE POSITIVE SUM IN Lp SPACES*

Jingjing HAO(郝晶晶)

School of Mathematical Sciences，Nankai University，Tianjin 3000r1，China E-mail : 27186963@qq.com

Yunbai DONG(董云柏)*

Hubei Key Laboratory of Applied Mathematics，Faculty of Mathematics and Statistics,Hubei University，Wuhan 430062，China E-mail : baigunmu301@126.com

Lei LI (李磊)

School of Mathematical Sciences and LPMC，Nankai University， Tianjin 3000711，China E-mail : leilee@nankai.edu.cn

Can φ be extended to a positive linear map from E onto F?

Zhang, Tsai and Wong [7] studied the norm-additive maps when E and F are strictly convex smooth Banach lattices and Lp(µ) spaces (1 ＜p ≤∞). Later, they answered the question for when E and F are non-commutative Lp-spaces Lp(M),Lp(N) associated to von Neumann algebras M and N, respectively [8].

For the sake of simplicity, we only consider real vector spaces and assume that the measure space (Ω,Σ,µ) in this paper is finite. For 1 ＜p ＜∞, we will use Lp(Ω1)+to denote the positive cone of Lp(Ω1) and S(Lp(Ω))+to denote the set

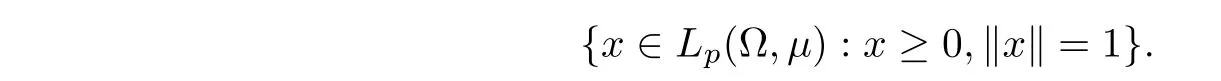
For any element x ∈S(Lp(Ω))+, let supp(x) be the set {ω ∈Ω : x(ω) /= 0}. Here, supp(x) is determined up to a measure zero set, as usual.

For the remainder of this paper,we will assume that(Ω1,Σ1,µ)and(Ω2,Σ2,ν)are measure spaces and that V0:S(Lp(Ω1))+→S(Lp(Ω2))+is a norm-additive bijection; that is,

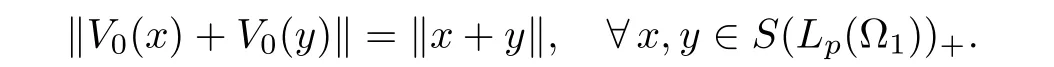
We will show that V0can be extended to be a surjective isometry from Lp(Ω1) onto Lp(Ω2).

2 Main Results

It is easy to get the following result:

Here, χAdenotes the indicator function of the measurable set A. Let G1= {supp(x) : x ∈S(Lp(Ω1))+} and G2= {supp(x) : x ∈S(Lp(Ω2))+}. Since Ω1,Ω2have a finite measure,Gi=Σifor i=1,2.

Lemma 2.2 There exists a regular set isomorphism σ from G1to G2such that

Proof Suppose that x,y ∈S(Lp(Ω1))+satisfies supp(x) = supp(y), subject to measure zero errors. For any z ∈S(Lp(Ω1))+, it follows from Lemma 2.1 that supp(z)∩supp(x) has measure zero exactly when supp(V0(z))∩supp(V0(x)) has measure zero. It follows from the bijectivity of V0that the complement of supp(V0(x)) does not intersect supp(V0(y)), and the converse is also true. This implies that supp(V0(x))=supp(V0(y)), up to a measure zero set.

Thus we can define a mapping σ from G1to G2such that

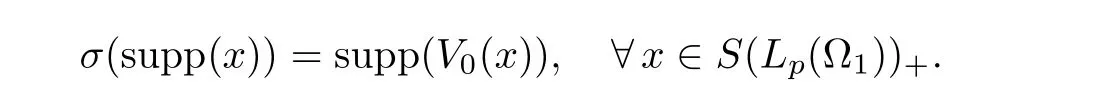
In a fashion similar to the argument of [7, Proof of Theorem 3.3], one can derive that σ is a regular set isomorphism. □

Remark 2.3 The same argument as to that in the proof of Lemma 2.2 indeed shows that supp(V0(x))⊂supp(V0(y)) whenever x,y ∈S(Lp(Ω1))+with supp(x)⊂supp(y). Here, the set inclusions are also valid, subject to measure zero errors.

Lemma 2.4 For any x ∈Lp(Ω1)+and A ∈G1, we have that

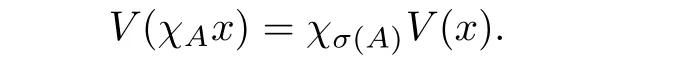
Proof If µ(A ∩supp(x)) = 0 or supp(x) ⊂A, the conclusion is true. Otherwise, define B =supp(x)A. Then B ∈G1and its measure is positive. Since V is positive homogeneous,we can assume that ‖x‖=1. Put

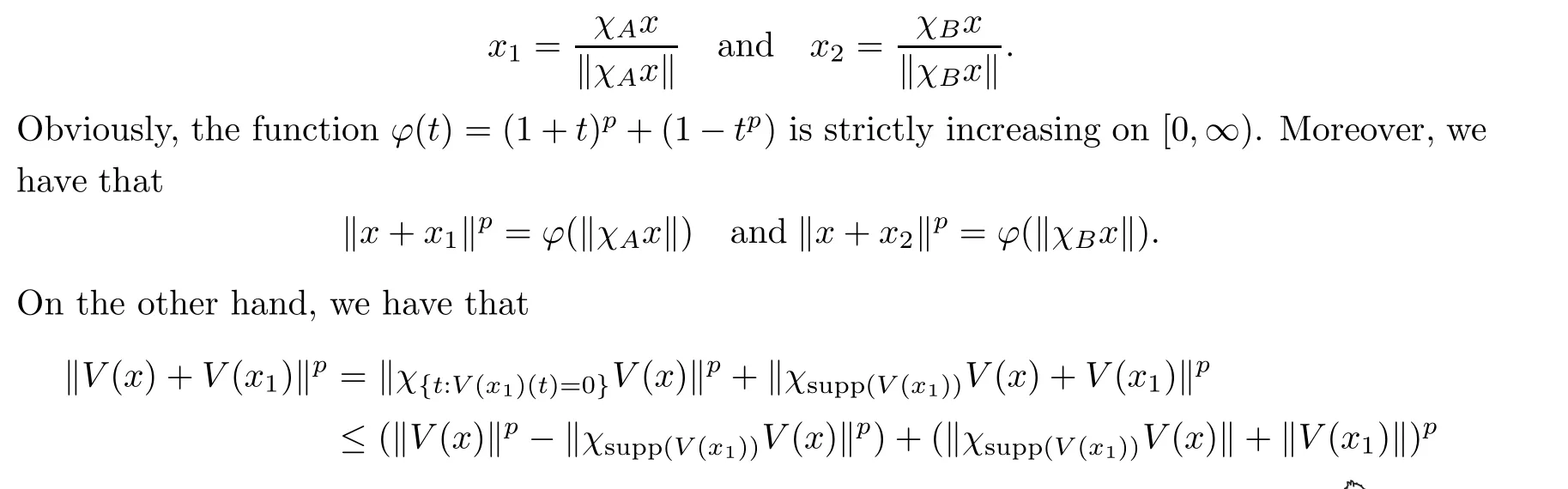
(2) Say that there exist disjoint sets A1and A2with positive measures such that A=A1∪A2. Pick z0∈Lp(Ω1)+such that supp(z0) = A. Then one can derive that supp(χAiz0) = Ai

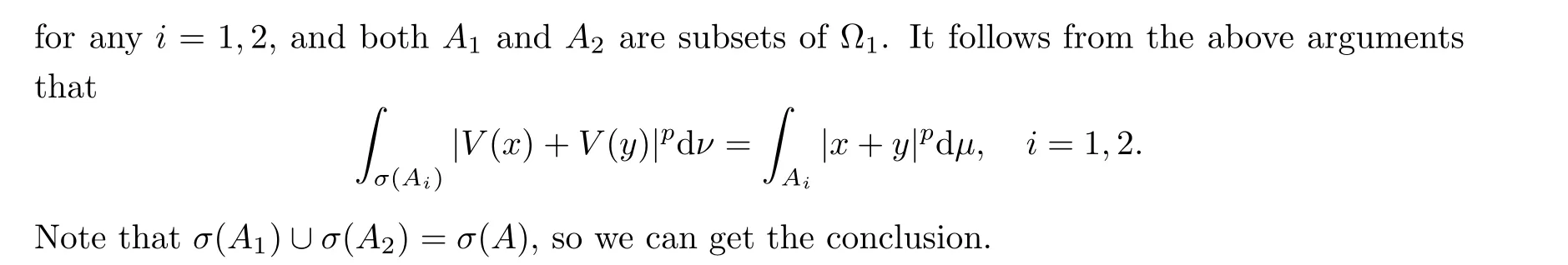
(3) The assertion is trivial when A is an atom. □

Recall that if (Ω,Σ,µ) is a measurable space, then E ⊂Ω is said to be locally measurable if for every measurable set A with finite measure, E ∩A is also measurable. A function f is locally measurable if it is measurable with respect to the σ-algebra generated by the locally measurable sets. The idea of the following proof is from [7]:

Theorem 2.6 Suppose that the bijection V0: S(Lp(Ω1))+→S(Lp(Ω2))+is normadditive. Then V0extends to a surjective linear isometry from Lp(Ω1) onto Lp(Ω2). More precisely, σ induces a surjective linear map ψ : Lp(Ω1) →Lp(Ω2) and a locally measurable function h on Ω2such that

Since V(χA) and V(χΩ1A) have disjoint supports up to measure zero errors, V(χA)(t) agrees with h(t) whenever V(χA)(t) is not zero (ν-a.e.). Therefore,

for any positive simple function z on Ω1such that 0 ≤z ≤x. Since x can be approximated from below by positive simple functions, we see that ‖V(x)-x‖=‖x-x‖=0. Therefore, in the original setting, we can derive that V(x)=hψ(x) for any x ∈Lp(Ω1)+. □