页岩纳米级孔隙甲烷渗透特性模拟

张朋旗，吴家全，王桂珠，张永康，郭丽梅

（天津科技大学 化工与材料学院，天津 300457）

随着常规油气资源的减少，页岩气等非常规资源的勘探和开发成为了新的研究热点。页岩气藏主要由基质（有机质、无机质） 和天然裂缝组成，且绝大部分有机质和无机质中的孔隙均为纳米级孔隙[1]。而气体在纳米级尺度中流动时，往往会出现微尺度效应。Knudsen数（Kn）是微尺度流动的特征参数，根据Kn可将流动划分为4个区域[2]：连续介质区Kn≤0.001，流体可视为连续介质，采用无滑移的Navier-Stokes（N-S）方程描述；滑移区0.001≤Kn≤0.1，流动存在微尺度效应，仍可视为连续介质，采用滑移边界的N-S方程描述；过渡区0.1≤Kn≤10，连续介质假设不再成立，可采用Burnett方程描述；自由分子流区Kn≥10，主要采用分子动力学方法进行研究。对于微尺度气体流动的研究，目前常用的方法有分子动力学方法、直接模拟蒙特卡洛方法和格子Boltzmann方法等[3]。由于格子Boltzmann方法具有编程简单，易于并行计算，且能够处理复杂边界条件的优点，近几年在页岩气数值模拟研究领域得到广泛的应用。

本工作通过四参数随机增长法构造二维多孔介质模型，采用格子Boltzmann方法模拟甲烷在多孔介质中的流动，研究了多孔介质孔隙率（ε）、进出口压差和吸附解吸对于甲烷气体渗透率（K）的影响。

1 模型的建立及边界条件

1.1 基本模型

采用D2Q9格子Boltzmann-BGK[4]模型，如图1所示。

图1 D2Q9模型Fig.1 D2Q9 model.

通过BGK近似、时空离散和速度离散，得到完全离散化的格子Boltzmann-BGK方程[4]，见式（1）。

局部平衡态分布函数见式（2）。

模型的速度配置见式（3）。

式中，c为格子速度，c=δx/δt。

模型的宏观密度、压力和速度定义见式（4）～式（6）。

1.2 松弛时间与Kn

Kn为页岩中的气体流动特征参数，需要通过Kn确定松弛时间[5]，见式（7）。

式中，L为计算域的特征长度。

Kn是模拟的关键数据[6]，由式（8）计算得出。

式中，d为分子的直径，m；m为分子的质量；H表示计算域高度；χ为矫正因子。

ψ（Kn）为矫正函数，由Guo等[7]提出，见式（9）。

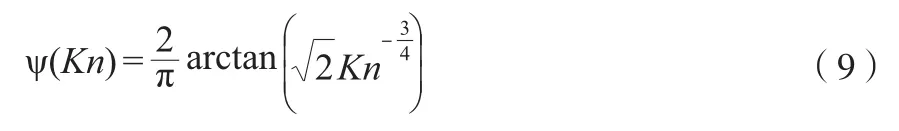
Yao等[8]考虑到气体致密性的影响，将松弛时间进行更进一步修正，见式（10）～式（12）。

1.3 边界条件

边界条件在页岩气模拟中起着重要作用，页岩气在通道中流动时，必须考虑在壁面上的吸附/解吸及扩散等现象，通过格子Boltzmann方程边界条件体现微尺度效应的影响。在一些研究中，在格子Boltzmann模型的边界条件中引入Langmuir吸附等温线，以呈现页岩中的吸附/解吸情况[9]。

本工作采用假定速度（us）来表示微观尺度下页岩基质中气流的滑移效应[10]，见式（13）。

α为吸附气体分子占比，见式（14）。

气体扩散时，吸附气在壁面发生表面扩散，自由气在空隙中产生分子扩散，在此模型中，用Fick定律计算吸附气和自由气的流量，见式（15）。

吸附气引起的壁面速度[11]，见式（16）。

β为Langmuir分配系数，由式（17）计算。

考虑气体在壁面处的滑脱情况，引入混合反弹边界条件[12]，见式（18）。

式中，fi'为标准反弹分布函数；fi''为镜面反弹分布函数。

反弹系数（Rb）[5]，由式（19）计算。

式中，σ=1，B1=1-0.181 7σ，B=0.8，σv=(2-σ)/σ。

将Langmuir等温吸附方程引入本模型的边界条件中，需对平衡态分布函数以及非平衡态分布函数进行组合，得到新的分布函数，根据Chapman-Enskog方法，定义壁面处的分布函数[12]，见式（20）。

式中，η=1/（τ+0.5）。

壁面处密度分布函数见式（21）。

式中，i=0～8。

而进出口边界采用Zou-He边界模型[12]，流体在通道内靠两端压差驱动，孔道入口端和出口端的分布函数见式（22）～式（27）。

入口端：

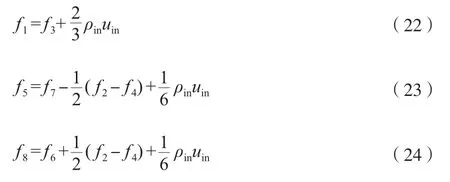
出口端：

2 模拟结果及讨论

2.1 四参数随机增长法构造多孔介质

采用Wang等[13]提出的随机生长四参数生成法（QSGS）构造多孔介质微观结构。该方法可通过参数调整控制生长介质的形貌特征。构造二维多孔介质时，令固体颗粒为生长相，孔隙为非生长相。实验过程如下：1）在构造区域内的网格上以中心核生长概率（cdd）随机配置生长相的生长核，cdd要小于ε；2）按照不同方向上给定的生长概率（dj）（j=1，2，…，8，j为生长方向），固相生长核向周围邻点生长；3）重复步骤2），直到非生长相达到给定的ε。

模拟储层区域压力约30 MPa，温度约80 ℃，页岩孔径分布范围在5～150 nm之间[14]，油层气主要成分为甲烷，在此条件下的密度为166.782 2 kg/m3，声速为622.823 5 m/s，黏度为1.298 43×10-7m2/s。网格步长（δx）在实际空间的长度为0.72 nm，设置实际模拟区域长约200 nm，宽约100 nm，建立几种不同ε的多孔介质模型，见图2。

2.2 页岩气微尺度流动模拟及影响因素

气体在纳米孔隙中的流动受很多因素影响，不同页岩气藏的ε、进出口压差和吸附作用差异较大，这些差异造成了不同页岩气藏中气体渗流规律的不同，理清这些因素对微尺度气体流动的影响机制具有重要意义。K是表征多孔介质流的重要参数及衡量标准，根据达西定律得到K的计算公式，见式（28）。

2.2.1ε对页岩气流动的影响

采用甲烷为模拟页岩气，将模拟进出口压差设为 0.4 MPa，Langmuir压力（PL）为 10 MPa，Langmuir体积为1.7 m3/t，表面扩散系数（Ds）为1×10-6m3/s，吸附气密度为游离气密度的2倍。图3为不同ε下流体的流速分布。

通过四参数随机增长法构造了不同ε的多孔介质模型，由于不同ε下流通通道的不同，导致了Kn及Rb等的差异，ε对页岩气流动有很大的影响。图4为不同ε下的K。由图4可知，随着ε的降低，K也随之降低。ε高时，孔道连通效果好，孔隙半径大，有利于流体流动，因此流速会高，K也大；而ε低时，孔道情况会变得复杂，孔隙半径变小，平均流速会减小，导致K减小。

2.2.2 压差对页岩气流动的影响

页岩气开采过程中的驱动力主要是地层的压力，而地层环境复杂，导致压差分布不均，因此需考虑压力对页岩气流动的影响。本工作采用压力驱动模型，进出口为Zou-He压力边界，出入口压力由密度确定，当ε=0.7时，模拟页岩气在不同压差下的K，结果见图5。

图2 多孔介质模型Fig.2 Porous media model.Porosity(ε)：a 0.9；b 0.8；c 0.7；d 0.6

图3 流速分布Fig.3 Flow velocity distribution.ε：a 0.9；b 0.8；c 0.7；d 0.6

由图5可知，随着进出口压差的增大，K也增大。进出口压差增大，流体流动的推动力增大，流体流速提高，K会升高，但在进出口压差变得很大时K才会有显著的提高。

2.2.3 吸附/解吸、扩散对页岩气流动的影响

页岩气开采过程中吸附/解吸、扩散等微尺度效应对油气运移具有一定影响，在模拟时通过边界条件体现，需综合考虑PL、Ds、吸附气密度等诸多因素的影响。分别模拟了吸附气密度确定时PL与Ds变化及PL确定时Ds与吸附气密度变化对K的影响，考察微纳米孔隙内甲烷气体吸附/解吸、表面扩散对流动的影响，结果见图6。

图4 不同ε下甲烷的KFig.4 Methane permeability(K) at different ε.

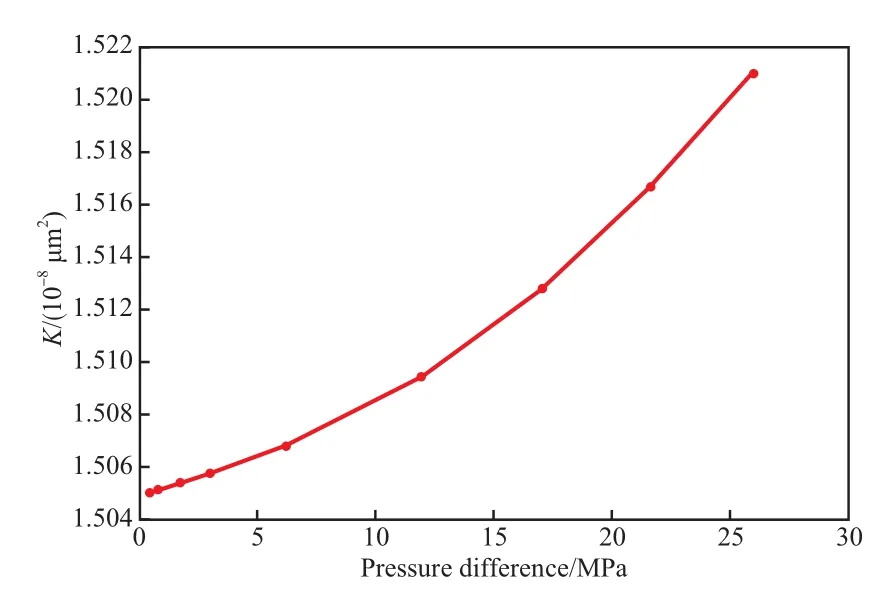
图5 不同压差下甲烷的KFig.5 K of methane at different pressure differences.

图6 不同Ds/Dk下甲烷的KFig.6 K of methane at different Ds/Dk.Ds：surface diffusion coefficient；Dk：molecular diffusion coefficient；Cμ：adsorbed gas concentration；C：free gas concentration；PL：Langmuir pressure.a Cμ/C=5；b PL=10 MPa

由图6可知，在吸附气浓度不变时，随着Ds与分子扩散系数（Dk）比值的提高，K会下降，而PL提高时，K也降低；在PL不变的情况下，吸附气浓度提高时，K下降，但两种情况下K下降幅度都不大。在页岩气流动时，PL和Ds只影响页岩气的壁面速度，而壁面速度的微小改变不会对整体K造成太大的影响。

3 结论

1）页岩气开采过程为微纳米孔径内的流动，使用格子Boltzmann方法可很好地模拟甲烷在多孔介质中的流动。

2）模拟页岩气在多孔介质中的流动时需考虑Kn及吸附/解吸的影响。

3）多孔介质ε对K的影响最为明显，ε越高越有利于甲烷流动；压差也会对K产生影响，压差大时驱动力大，有利于甲烷流动。甲烷在页岩表面的吸附/解吸会对壁面速度产生一定影响，但对整体K的影响不大。

符 号 说 明