一般计数资料Poisson分布模型回归分析

胡良平

(1.军事科学院研究生院，北京 100850； 2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

1 一般计数资料及其Poisson分布模型构建原理

1.1 一般计数资料Poisson分布回归模型的形式

1.1.1适于一般计数资料Poisson分布回归模型的数据结构

适于一般计数资料Poisson分布模型的数据结构见表1[1]。

【对数据结构的分析】因变量Y为“计数变量”，其均值为7.467、方差为13.016，方差稍大于均值，只能将Y近似视为服从Poisson分布的离散型随机变量(理论上，均值应等于方差)；拟考察的三个自变量均是“二值变量”，在回归分析中是可以接受的，但在统计学理论中，默认自变量为“计量变量”。

1.1.2 Poisson分布概率函数[2]

设Y是一个服从Poisson分布的随机变量，X=(1,x1,x2,…,xq)'是一个协变量向量，β=(β0,β1,β2,…,βq)'是参数向量。如果Y的数学期望的对数可以表示为协变量的线性表达式，即E(Y|X)=exp(X'β)=或ln[E(Y|X)]=X'β，则称(Y，X)服从Poisson分布回归模型。对应的表达式见下面的式(1)：

(1)

表1 三个可能的影响因素(X1-X3)对30例非气质性心脏病且仅有胸闷症状就诊者24小时早搏数Y的观察结果

注：Y，24小时中早搏数；X1，是否吸烟(1-吸烟、0-不吸烟)；X2，是否喝咖啡(1-喝、0-不喝)；X3，性别(1-男、0-女)

1.1.3 一般计数资料Poisson分布回归模型的表达式

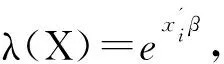
(2)

值得注意的是：统计软件给出的计算结果是下面式(3)等号右边回归系数的估计值。也就是说，Poisson分布回归模型的“核心部分”是其“期望值(或称均值)”，用自变量的线性组合来表达计数因变量Y的期望的自然对数。

ln[λ(X)]=β0+β1x1+β2x2+…+βmxm+ε

(3)

式(3)中的“ln”代表“自然对数函数”，λ(X)代表服从Poisson分布的离散型随机变量Y的均值，X代表所有自变量构成的“向量”，ε代表模型的误差。有些统计学教科书将式(3)称为“Poisson分布回归模型”，这是不够准确的。它应被视为“Poisson分布回归模型”的“内核”，即“核心内容”，外文文献中称其为“Poisson分布回归模型”的“连接函数”。

1.2 一般计数资料Poisson分布回归模型的求解

1.2.1 求解参数的思路

如何求解出式(3)中的回归系数呢？首先，应该明白：λ(X)是X的函数，在实际资料中是无法观测到的，它随着X取值的改变而变化，是一个“隐变量”；回忆求解多重线性回归模型中的参数时所面临的“处境”，在那里，计量因变量Y的取值是可以观测到的，是“显变量”[3-6]。

显然，直接根据式(3)无法求出式中的回归系数。需要基于式(2)并采用“最大似然法”[7]构造“目标函数”，运用高等数学方法，将“目标函数”转变成“方程组”，再运用“计算数学”或“统计计算”等技术方法求解“方程组”。由于方程组为“非线性方程组”，一般没有直接解，需用到迭代计算法，如加权最小二乘迭代或牛顿-纳法生迭代法。从而获得式(3)的“参数估计”结果。因篇幅所限，参数估计公式的详细推导过程从略。

1.2.2 Possion回归系数的假设检验

1.2.2.1 似然比检验

通过比较两个相嵌套模型(如模型P嵌套于模型K内)的对数似然函数统计量G(又称Deviance)来进行，其统计量见式(4)：

G=GP-GK=-2× (模型P的对数似然函数-模型K的对数似然函数)

(4)

其中，模型P中的变量是模型K中变量的一部分，另一部分就是需要检验的变量。这里，G服从自由度为K-P的χ2分布。

1.2.2.2 回归系数的Wald检验

比较估计系数与“0”的差别是否有统计学意义，其检验统计量见式(5)：

(5)

这里z为标准正态变量。参数的置信区间是基于Wald统计量导出的。β的95%置信区间见式(6)：

(6)

1.2.3 Possion拟合优度检验

1.2.3.1 Deviance偏差统计量

设L(bmax;y)为全模型的似然函数，L(b;y)为选模型(含部分自变量的模型)的似然函数，则定义λ统计量见下面的式(7)：

λ=L(bmax;y)/L(b;y)

(7)

计算Deviance偏差(D)统计量，采用公式(8)：

D=2lnλ=2[lnL(bmax;y)-lnL(b;y)]

(8)

且D服从χ2分布。很显然，D越大，模型的估计值与观测值的偏差就越大，拟合效果就越差。

1.2.3.2 广义χ2统计量

广义χ2统计量见式(9)：

(9)

2 一般计数资料Poisson分布回归模型的SAS实现

2.1 创建SAS数据集

利用下面的SAS数据步程序，创建名为“maop1006”的SAS数据集：

data maop1006;

input obs X1-X3 Y @@;

cards;

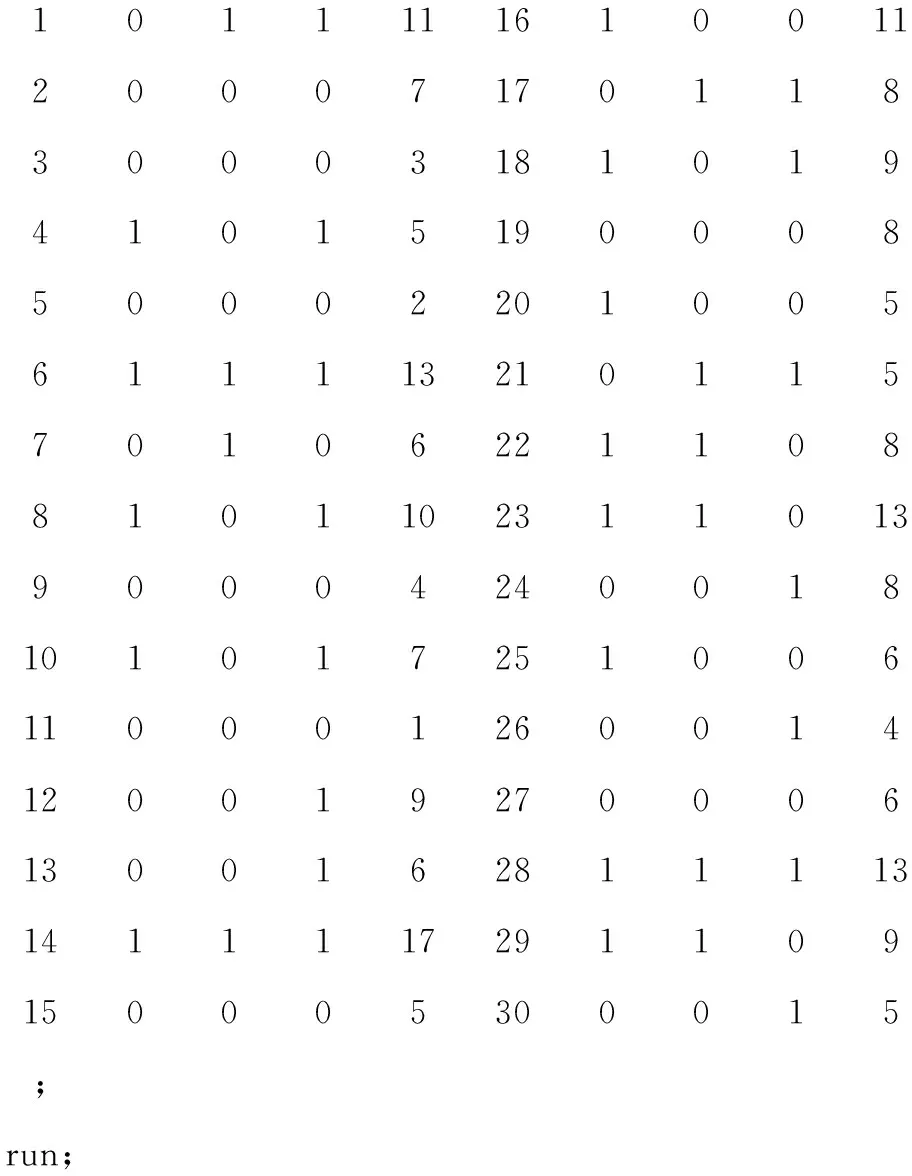
1011111610011 2000 717011 8 3000 318101 9 4101 519000 8 5000 220100 5 61111321011 5 7010 622110 8 8101102311013 9000 424001 810101 725100 611000 126001 412001 927000 613001 6281111314111 1729110 915000 530001 5;run;

2.2 求出因变量Y的均值与方差

利用下面的两个SAS过程步程序，求出因变量Y的均值与方差。

proc univariate data=maop1006 noprint;

var Y;

output out=aaa mean=ybar var=yvar;

run;

proc print data=aaa;

var ybar yvar;

run;

【SAS输出结果】

Obsybaryvar17.4666713.0161

求出Y的均值和方差分别为7.467、13.016。

2.3 基于全部自变量对因变量Y构建多重Poisson分布回归模型

利用下面的SAS过程步构建Poisson分布回归模型：

proc genmod data=maop1006;

model Y=X1-X3/link=log dist=poisson;

run;

【SAS程序说明】“link=log”表明采用“自然对数”作为连接函数，即对计数因变量取自然对数变换；“dist=poisson”表明要基于Poisson分布构建Poisson分布回归模型。

【SAS主要输出结果】

最大似然参数估计值的分析

以上结果表明：X3(性别)对因变量的影响无统计学意义。此结果是否正确，有待进一步研究。

2.4 在构建多重Poisson分布回归模型时检验因变量是否存在“过离散”现象

利用下面的SAS过程步程序构建Poisson分布回归模型，重点在于检验因变量是否存在“过离散”现象：

proc genmod data=maop1006;

model Y=X1-X3/link=log dist=nb noscale;

run;

【SAS程序说明】“dist=nb”说明指定资料中因变量(误差项)的分布为“负二项分布”；关键问题在于：只有指定为此分布时，才能发挥选项“noscale”的作用，它是将冗余参数k的取值固定为“0”，相当于进行Poisson分布回归分析，同时，采用拉格朗日(Lagrange)乘子检验“因变量是否存在‘过离散’现象”。

【SAS主要输出结果】

第1部分输出结果同上，从略。

拉格朗日乘数统计量参数卡方Pr > 卡方离散度8.63150.0017*

注：*单侧P值

以上结果表明：因变量确实存在“过离散”现象，构建Poisson分布回归模型时应对其进行校正。

2.5 在构建多重Poisson分布回归模型时对“过离散”现象进行校正

利用下面的SAS过程步程序构建Poisson分布回归模型，对“过离散”现象进行校正：

proc genmod data=maop1006;

model Y=X1-X3/link=log dist=poisson scale=deviance;

run;

【SAS程序说明】选项“scale=deviance”是要求对“过离散”进行校正后，再构建Poisson分布回归模型。

【SAS主要输出结果】

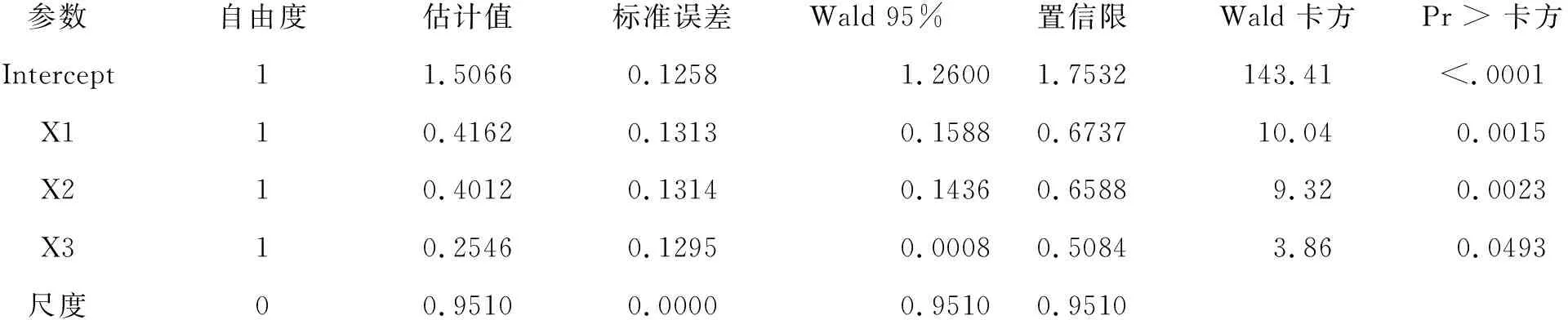
最大似然参数估计值的分析

以上结果表明，尺度参数由“1”调整为“0.9510”，由此，模型中各参数的“标准误”均得到“校正”。故最后两列的数值也都得到校正。经校正后，原来无统计学意义的“X3”变为有统计学意义。由以上结果可以写出Poisson分布回归模型中的“内核”：

ln[λ(X)]=1.5066+0.4162X1+0.4012X2+0.2546X3

λ(X)=e1.5066+0.4162X1+0.4012X2+0.2546X3

若将上面的λ(X)代入本文第1.1节中的式(2)，就可获得完整的“Poisson分布回归模型”。

【专业结论】因X1、X2和X3前的系数分别为exp(0.4162)=1.516189、exp(0.4012)=1.493616和exp(0.2546)=1.289946，又因为X1代表“是否吸烟(1-吸烟、0-不吸烟)”、X2代表“是否喝咖啡(1-喝、0-不喝)”、X3代表“性别(1-男、0-女)”，说明吸烟者出现早搏的概率是不吸烟者的1.516倍、喝咖啡者出现早搏的概率是不喝咖啡者的1.494倍，而男性受试者出现早搏的概率是女性受试者的1.290倍。