利用证据神经网络的多分类器系统构造

和红顺,韩德强,杨艺

(1.西安交通大学电子与信息工程学院,710049,西安;2.中国电子科技集团公司航天信息应用技术重点实验室,050004,石家庄;3.西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

复杂环境或场景下,单一分类器的分类效果往往不够理想[1]。多分类器系统[2]是应对复杂环境下模式分类问题的有效方法,已被广泛应用于图像识别[3]、语音识别[3]、医疗诊断[4]等领域。

学者们基于多分类器系统的多个层面开展了研究。在成员分类器生成层面,已有研究方法主要有选用不同训练样本获得成员分类器[5]及基于不同的分类算法生成成员分类器[6]等。由多个相同的分类器构成的多分类器系统,其性能并不会优于单一成员分类器[7]。如果多个成员分类器所提供的信息是互补的、有差异的,则融合分类性能一定会优于单一最优分类器,采用具有一定互补性[8]的不同成员分类器是多分类器系统提升融合分类性能的关键。一些学者分析了如何生成和选择具备互补性的成员分类器[9-10]。在多分类器融合规则方面,对成员分类器的不同输出形式采用不同的融合方式,如投票法[11]、Bayes法[12]以及DS证据理论法[13]等。

成员分类器的生成是多分类器系统设计的基础。神经网络是一类常用的分类器,其中BP神经网络是一种简单有效的分类算法。然而,在分类训练过程中,训练样本中往往存在很难准确判断类别归属的数据,即这些样本在分类时存在不确定性。证据理论是一种表示和处理不确定性的有效的工具。针对数据的不确定性问题,本文提出一种证据神经网络分类器并将其作为成员分类器来构造多分类器系统。首先对训练数据进行重组,将难以准确分辨类别的数据划归到新的类别(混合类),在建模过程中保留着训练数据本身含混性的这一不确定性。然后使用重组后含有混合类数据的训练集训练成员分类器,将得到的输出进行证据函数建模。最后用证据组合规则来融合多个成员分类器结果以提高多分类器系统的性能。实验结果表明,本文提出的多分类器系统合理、有效。

1 多分类器系统简介

1.1 多分类器系统概述

多分类器系统是一种应对复杂模式识别问题的有效方法,在模式识别领域得到了广泛的关注和应用。多分类器系统使用多个不同的分类器进行分类,然后通过一定的组合机制融合多个具有一定互补性[14]的分类器结果,以获得更加有效的分类效果。多分类器系统的流程如图1所示。

图1 多分类器系统流程图

系统基于成员分类器的不同输出形式选择合适的融合方式,融合成员分类器结果,得到最终的决策结果。成员分类器的输出为度量级(即输出为一系列代表各类别可能性的度量值)时,可以采用DS证据理论[15]等方法进行融合。

多分类系统能够一定程度上提高分类精度,但并非任意分类器组合都能获得这样的提升。不同成员分类器之间的互补性非常关键。

1.2 差异性度量

差异性度量[16]的目的是通过某种方法对分类器集合中各个分类器之间的差异进行量化。成对差异性度量较为常用。成对差异性度量需要考虑两两分类器之间的差异性,其代表方法有统计法、相关系数统计法、不一致度量法及双错法等。本文使用其中应用最多的不一致度量法。不一致度量法由于要计算两两基分类器之间的统计关系,因而依赖于两基分类器的联合分布。令分类器Si、Sj判断正确为1,判断错误为0,分类器输出统计量Nmn(m,n∈{0,1})表示分类器Si、Sj判断为m、n的样本个数,分类器Si、Sj的联合输出码如表1所示。

表1 分类器Si、Sj的联合输出码

不一致度量值表达式如下

(1)

对一个由L个成员分类器构成的成员分类器集的差异性度量值为成员分类器集中所有两两分类器差异性度量值的平均,表示如下

(2)

2 基于证据神经网络的多分类器系统

传统的神经网络的训练过程是基于“硬”标签(清晰的类别标签)的训练样本,而在真实数据中往往存在一些难以准确分类的样本。这部分数据在类别归属上存在着含混性,使用传统的神经网络直接对这些数据进行分类往往容易得到错误的结果。证据理论,又称为信度函数理论,是处理这种含混的不确定性的有效工具[17-22],因此本文利用证据理论对神经网络分类器训练数据本身存在的不确定性进行建模表征和处理,使用证据组合规则融合多个分类器结果来减少或消解不确定性,以求得到更好的分类性能。

2.1 证据理论简介

在证据理论中,设集合Θ={θ1,θ2,…,θn}为辨识框架,2Θ是Θ所有子集的集合。若m:2Θ→[0,1]满足

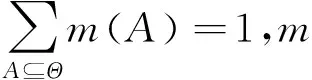
(∅)=0

(3)

则称m为辨识框架上的基本信度赋值(BBA),也称mass函数。若∀A⊆Θ,m(A)>0,A被称为焦元。

对于辨识框架Θ中的某个命题A,其信任函数和似真函数的定义分别为bel(A)和pl(A),表示如下

(4)

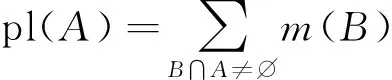
(5)

区间[bel(A),pl(A)]用于表示A的不确定性。

Dempster组合规则用于独立证据间的组合。辨识框架Θ上的2个独立证据的mass函数为m1和m2,对于∀A⊆Θ,A≠∅,依据Dempster组合规则如下

(6)

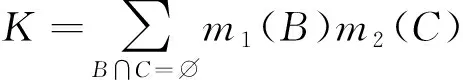
Dempster组合规则在高冲突证据组合中会得到反直观的结果,为了解决这一问题,一些研究者提出了一些改进的方法,其中具有代表性的有Yager组合规则和Murphy组合规则。

Yage认为证据冲突部分代表了不可靠信息,应该被赋给全集,以表征“未知”[23],规则定义为

(7)

Yager规则满足交换律,但不满足结合律。

Murphy首先采用了等权值的方式得到平均证据[24],假设有s个证据,则平均证据为

(8)

然后应用Dempster组合规则对平均证据mave自身组合s-1次。其他一些组合规则详见文献[25]。

在得到融合证据后,由证据至概率的转换是实现融合决策的重要步骤。Smets定义的Pignistic概率转换[15]用于将mass函数转换为概率

(9)

2.2 证据神经网络多分类器系统

证据理论中证据函数的生成,特别是混合焦元的确定是难点所在。传统的神经网络训练过程是基于“硬”的类别标签,如图2a所示,用传统的神经网络来生成证据函数只能得到单点的焦元[26],无法发挥证据理论的优势,不能对含混性进行建模和表征。而本方法得到的输出包含单点焦元和混合焦元,如图2b所示用神经网络对包含混合类数据的训练数据进行训练,可以得到包含混合焦元在内的多个焦元,能够有效的表征数据的含混性。这里以BP神经网络(三分类问题)为例,阐述本文方法的具体实现。

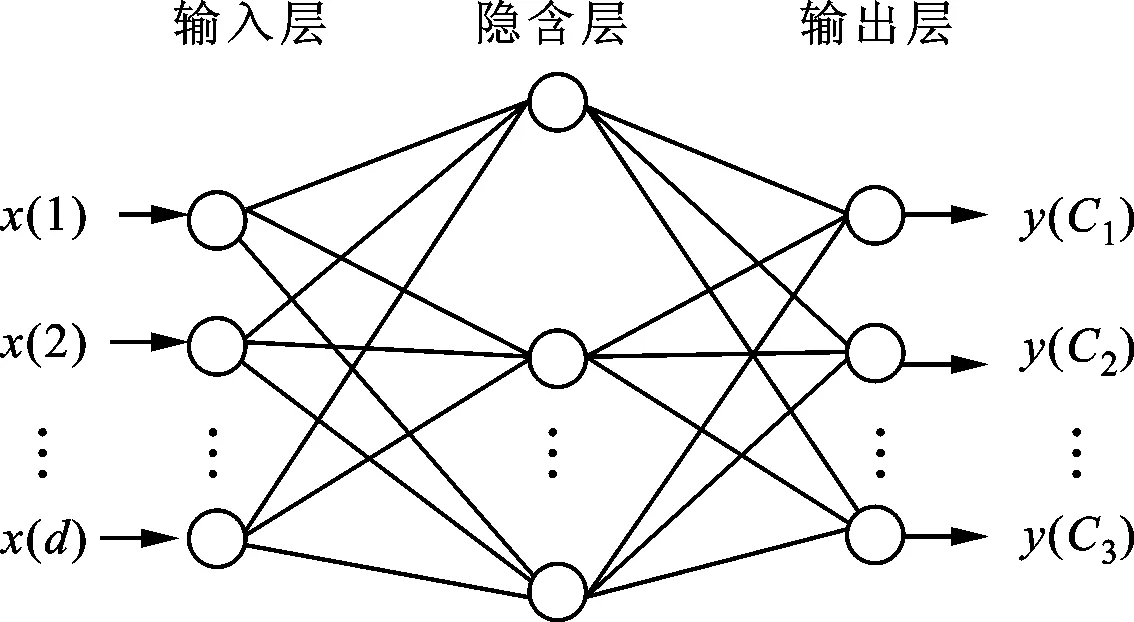
(a)传统神经网络分类器

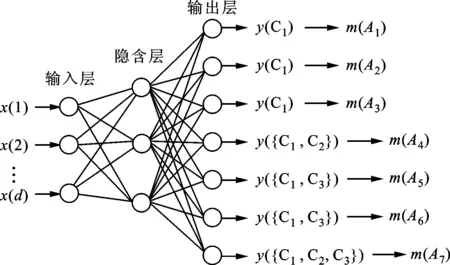
(b)证据神经网络分类器图2 证据BP神经网络分类器

假设训练数据有3类,类别标签为C1、C2、C3。首先对原有的训练样本进行重组,得到包含混合类在内的新训练样本,共23-1=7个类别,分别为{C1}、{C2}、{C3}、{C1,C2}、{C1,C3}、{C2,C3}、{C1,C2,C3}。给定任意一个测试样本,采用后向传播(BP)神经网络得到的焦元以及所对应的mass赋值,如表2所示。

表2 证据神经网络焦元及所对应的mass赋值

mass赋值形式如表2的神经网络称之为证据神经网络。当数据含有M个类别时得到2M-1个mass赋值。信度分配方式为对于输入的训练样本x={x(1),x(2),…,x(d)},将神经网络的输出结果归一化为

(10)

式中:y(Ak)为测试样本输出。得到证据函数m(Ak),表示BP网络在重组后的数据属于第k个命题Ak的基本信任分配。举例说明,设测试样本输出为y(A1)=0.5、y(A2)=0.3、y(A3)=0.3、y(A4)=0.2、y(A5)=0.2、y(A6)=0.3、y(A7)=0.2,利用式(10)归一化得到一组证据函数m(A1)=0.25、m(A2)=0.15、m(A3)=0.15、m(A4)=0.1、m(A5)=0.1、m(A6)=0.15、m(A7)=0.1。图2为传统神经网络分类器与BP神经网络分类器的网络结构对比示意图。

需要指出的是,传统的神经网络是基于“硬”的清晰类别标签的,而本文中的方法是采用混合类作为标准输出,在证据建模的过程中不随意丢弃数据含混的这一确定性,构造复合焦元(包括焦元组成及mass函数赋值),通过构造多个成员分类器并用证据理论方法融合来减少或消解这种不确定性,以求达到更好的分类效果。

在对训练数据进行重组中最关键的一点是如何去定义混合类。

2.3 混合类的构建

本节介绍如何确定训练数据中的含混数据部分以及数据的重组过程。本文采用K近邻算法[27]和集合交并运算来确定混合类数据并完成训练数据的重组。

(1)对于二分类的训练数据,给定K值,遍历找出距离当前训练样本最近的K个样本,和当前样本标签一致的数据个数记为N1,与当前数据标签不一致的数据个数记为N2。当N2≥N1时,把当前样本划分到混合类部分。

(2)对于多分类问题,以3类问题为例,选取C1、C2类的混合部分数据M12(M12由用上述划分二分类混合类的方法得到,M13、M23也用同样的方法得到),最终的C1、C2类混合数据为S12=M12-M12∩M13-M12∩M23;同样的可以得到C1、C3类混合S13=M13-M13∩M12-M13∩M23和C2、C3类混合S23=M23-M23∩M12-M23∩M13。C1、C2、C3的混合类S123由下式得到

S123=(S12∩S13)∪(S12∩S23)∪(S23∩S13)

(11)

2.4 对不均衡数据的处理

训练数据重组之后往往会出现数据的不均衡。两类数据经过重组后的训练数据C1类数据、C2类数据远多于混合类{C1,C2}数据,如图3所示。不均衡数据直接进行分类往往效果不佳,需要进行均衡化的处理。

图3 训练数据重组后的分类数据不均衡状况

本文采用SMOTE过采样算法[28]均衡化数据。SMOTE算法是利用特征空间中现存少数类样本之间的相似性建立人工数据的方法。Smin表示当前的需要补充数据的原始样本集合,对于每一个样本xi∈Smin使用K近邻法,其中K是指定的整数。通过以下方法得到人工样本

(12)

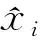
3 实验比较和分析

为了验证本文提出的证据神经网络多分类器系统的合理有效性,基于人工数据集和UCI数据集进对比实验。实验方法:依次选取原始数据的每三维特征构成一个子空间(最后一个子空间维度为原始特征维度除以3的余数),例如假设原始数据有8维特征{d1,d2,d3,d4,d5,d6,d7,d8},则可以得到{d1,d2,d3}、{d4,d5,d6}、{d7,d8} 3个特征子空间,将原始数据按列随机排序,同样的依次选取特征得到不同的子空间集合,将原始数据按列多次随机依次选取生成多个不同的特征子空间集合,来构造出多个不同的多分类器系统,利用成对差异性度量(式(2))选取其中差异性最大的子空间集合构造多分类器系统。实验将样本数据平均分成5份,任意选取其中的3份作为训练数据,其余2份数据作为待测数据,重复多次实验取平均正确率。实验中数据的每一维特征Fi都做归一化处理

(13)

需要指出的是,在使用本文提出的证据神经网络多分类器时,使用的训练数据是重组后包含混合类的训练数据(均衡化后)。

本文实验使用了多种不同的融合规则进行对比,其中不同的融合规则对应的本文方法的简称如表3所示。

表3 本文设计的3种分类器系统方法的融合规则及简称

在同等条件下,将本文提出的方法(MNE-DS、MNE-Yager、MNE-Mur)与投票法(MaVot)和贝叶斯BBA(BBBA)方法进行对比。投票法[29-30]是一种简单有效的融合方式,已广泛的应用于多分类器系统中。贝叶斯BBA(只含有单焦元的BBA)是将BP神经网络的输出归一化,再使用融合方法进行融合。

3.1 人工数据集

本文构造的人工数据集共3类,每个样本包含6个独立的特征维度。第1、2维度,3、4维度,5、6维度的数据分别由下式得到

(14)

式中:r是[01]的随机数;αk(k=1,2,3)为给定常数;θ为一个随机角度。人工数据集Da可以表示为Da=[x1(1),x1(2),x2(1),x2(2),x3(1),x3(2)]。

每一类数据包含100个样本,样本每个维度对应的αk的值如表4所示。

表4 不同维度数据3个类别所对应的αk值

本文构造的人工数据如图4～图6所示。本文分别使用训练数据的1、2维度,3、4维度,5、6维度这3个子空间训练成员分类器来构造多分类器系统。从图4～图6可见,第1个子空间上C1、C3类数据是容易区分的,第2个子空间上C1、C2类数据是容易区分的,第3个子空间上C2、C3类数据是容易区分的。这3个子空间有一定的差异性。

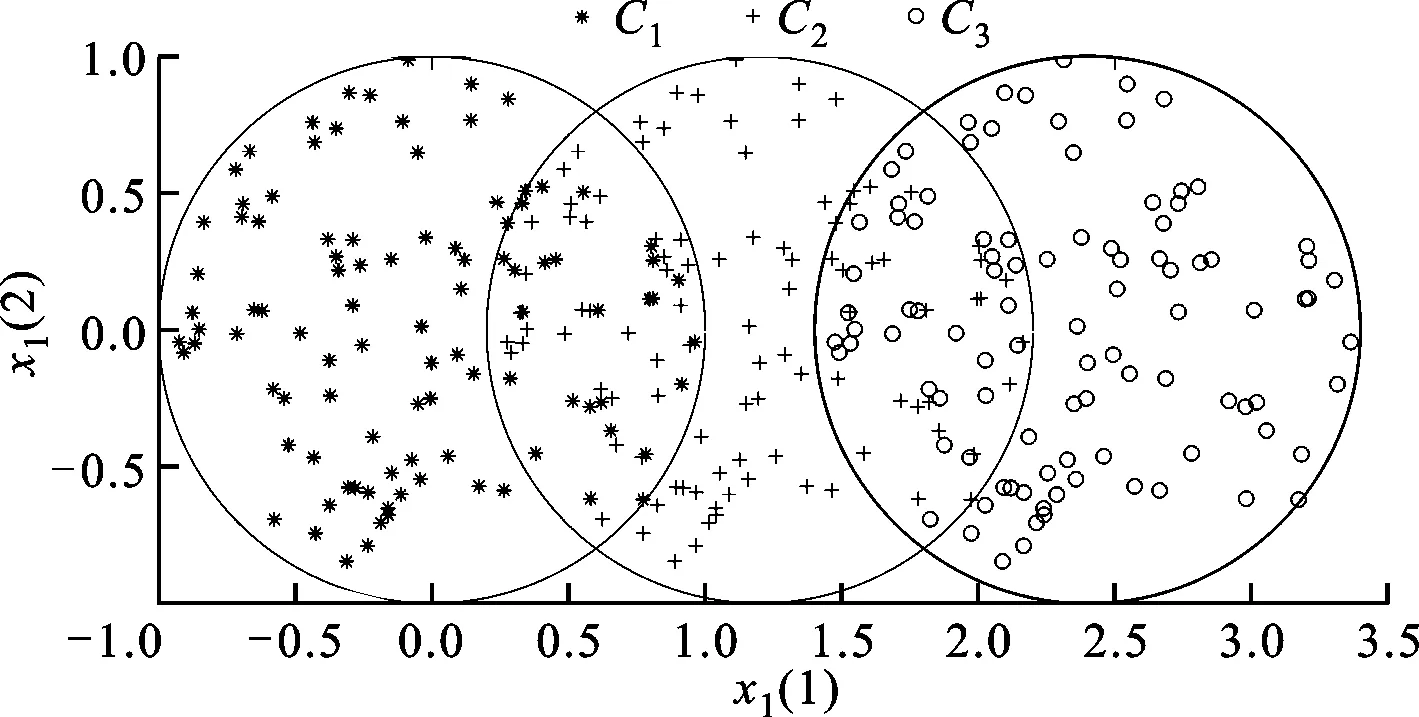
图4 人工数据集1、2维度特征

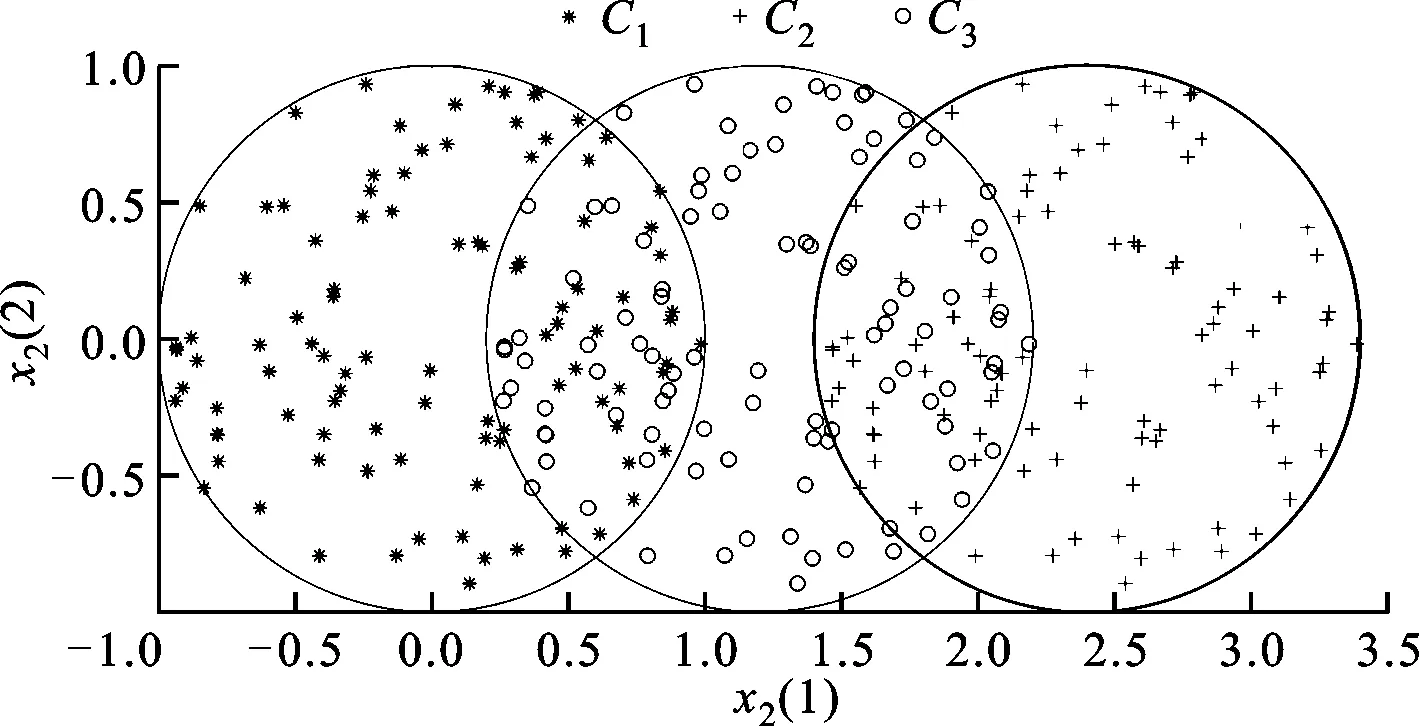
图5 人工数据集3、4维度特征

图6 人工数据集5、6维度特征

人工数据集下多分类器系统的平均分类正确率如表5所示。由表5可见,本文提出的方法MNE-DS、MNE-Yager、MNE-Mur相比于投票法、Bayes BBA方法可以得到更好的分类效果。

表5 人工数据集下多分类器系统的分类效果比较

3.2 UCI数据集

实验使用的UCI数据集信息如表6所示。本文依次选取原始训练数据的维度特征构成子空间,将原始训练数据按列随机排序,用同样的依次选取方法可以得到不同的子空间集合。重复上述操作生成30个不同的特征子空间集合,用得到的不同的子空间集合训练得到多个不同的多分类器系统,利用成对差异性度量(式(2))选取其中差异性最大的子空间集合构造多分类器系统。

表6 实验所用UCI数据集信息

采用本文提出的3种算法(MNE-DS、MNE-Yager、MNE-Mur)与投票法(MaVot)和Bayes BBA(BBBA)方法进行对比,结果如表7所示。从表7可以看出,本文提出的证据神经网络多分类器有很好的分类效果,在数据集Diabetes和Seeds分类正确率明显高于其他多分类器系统。一般而言,对于证据神经网络多分类器,类别数据多且特征维

数低时,数据的不确定性比较突出。在二分类数据集Pima、Magic 04和Diabetes上,特征维数属于中低水平,相比投票法,证据神经网络多分类器分类正确率有明显的提高,在特征维度很高的Wdbc数据集上分类正确率有一定程度的提高;在三分类数据集Seeds和Iris上,数据的特征维度较低,类别数目较高,说明证据神经网络多分类器系统具有很好的分类性能。

总体而言,本文提出的证据神经网络多分类器在继承了传统神经网络良好的分类性能的同时,充分利用了数据间含混的不确定性,并利用证据组合规则融合来消解这一含混的不确定性,从而得到更好的分类效果。

4 结 论

本文提出了一种基于证据神经网络的多分类器系统,该系统在建模过程中保留数据的含混性并尝试用证据理论去消解这一含混的不确定性。本文基于证据神经网络的多分类器系统能更加充分地利用训练数据所包含的信息,相比于其他基于神经网络的多分类器系统如基于投票法的多分类器系统以及基于贝叶斯BBA的多分类器系统,在建模过程中能更为有效的避免信息的丢失,得到的识别结果具有更高的可靠性,进一步提高了分类正确率,得到的分类效果更为准确。

在今后的研究中,我们将尝试使用其他类型的有监督神经网络分类器构造多分类器系统,以及探寻更为合理有效的划分混合类数据的方法,更为科学地完成训练数据的重组过程。差异性度量是多分类器系统的一个重要部分,近来取得了一些进展,在将来的工作中,我们将在本文方法的基础上设计更为科学有效的差异性度量方法,构造出更为科学可靠的多分类器系统,以求得到更为准确的分类结果。

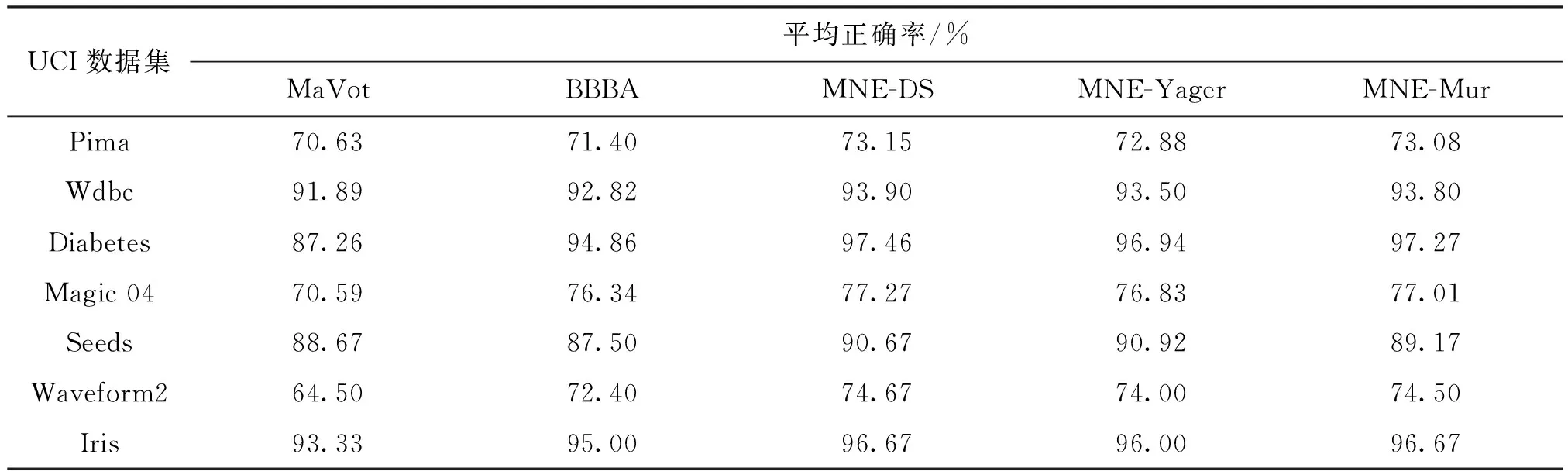
表7 本文3种算法与其他2种算法在UCI数据集上的分类效果比较