采用仿鱼形叶片的多翼离心风机性能研究

熊仲营,王梦豪,刘小民,李典,王雷

(西安交通大学能源与动力工程学院,710049,西安)

鲹科鱼类在自然进化过程中形成了多种多样的外形和高效、快速的游动性能。虽然不同鱼类物种的外形存在一定的差异,但都具有类似半椭圆、抛物线型回转体结构,这种流线型结构具有较好的流场阻力特性。研究表明,鲹科鱼类在C形转弯过程中通过身体的快速弯曲产生一个涡对,然后尾部向身体另一侧运动,使涡向尾部移动并到达尾柄处(尾鳍和身体的结合处)脱落,通过尾鳍对其进行控制,使涡最终汇入尾迹区,在这C形转弯过程中没有任何其他涡的脱落,从而不产生鱼体分离阻力[1]。多翼离心风机由于尺寸小、流量系数高、噪声低的特点多被应用在空调、吸油烟机和通风换气扇等家用电器中,而在多翼离心风机单圆弧叶片流道内,气流流经弯曲流道而流出叶轮区,叶片弯曲程度和鲹科鱼类身体弯曲时的姿态是相似的。

传统多翼离心风机性能提升的研究除了数值模拟和实验测量方法外,主要从多翼离心风机结构优化设计方面对风机气动性能和噪声进行了改进,并取得了一些好的效果。王斗提出了双圆弧叶片设计方法,较好改进了单圆弧叶片普遍存在的进口载荷大、气流分离严重的问题[2]。毛全有采用将叶片设计为沿叶高方向布置为梯形与矩形的分段设计方法,通过数值研究发现,采用分段设计的叶片的风机较原型风机效率提升了3.69%,同时风量增加了16.3%[3]。罗嘉陶等研究了CW-1和C-4翼型叶片,发现后缘被自然切除的叶片在翼型叶片表面有流线型设计,且前盘区域有较低的循环流量,可获得较大的风量和全压,较好适用于柜式空调中多翼离心风机的叶片设计中[4]。王湛对双圆弧叶片在不同的圆弧曲率及角度以及进口安装角等参数组合方式下的风机性能进行了模拟研究,分析表明双圆弧叶片的气动性能要优于单圆弧叶片[5]。伍先俊等通过对叶片进行穿孔,使得部分气流由叶片的高压面流向低压面,从而使涡流分离点移向叶片下方,这样可降低叶片的出口截面分离区的涡流强度和尺度,使噪声得到了降低,但该方法要求有较高的加工精度[6]。焦硕博等发现,采用倾斜叶片在出口角度不变时由于叶片发生扭转,相比直叶片会略降低风量,但可减小叶道内的流动分离[7]。Lin等采用NACA4412翼型改进了用于笔记本电脑中冷却风扇的叶片型线,缓解了叶片吸力面的流动分离,从而提高了风机效率,降低了噪声[8]。Liu等提取了苍鹰尾缘的锯齿结构,建立了用于多翼离心风机的尾缘锯齿结构的仿生叶片,研究表明,该仿生叶片有效降低了尾迹涡造成的气动噪声[9]。同时,Liu等对标准NACA0012翼型和长耳鸮40%展弦截面型线仿生翼型的多翼离心风机气动性能和噪声特性进行了研究,对比发现,仿生翼型既保证了风机气动性能,又有效降低了风机的涡流噪声和旋转噪声[10]。

(a)蜗壳和集流器 (b)叶轮图1 单进气式多翼离心风机结构

为了提高多翼离心风机风量,降低噪声,受鲹科鱼类机动游动姿态和涡流特征的启发,本文选取离心风机从头部到尾柄处进行弯曲,使其具有和多翼离心风机前弯叶片相似的弯曲结构。根据尺寸约束条件,设计了一种基于鱼体水平轮廓结构的前弯叶片,通过数值模拟方法考察仿鱼形叶片用于提高多翼离心风机气动性能的可行性,揭示了仿鱼形叶片提升多翼离心风机性能的原因。

1 计算模型建立及方法

1.1 物理模型

本文研究的通风换气装置中多翼离心风机为单进气形式,风机由蜗壳、叶轮及集流器组成,如图1所示,原型单圆弧叶片叶轮基本参数如表1所示。

表1 单圆弧叶片叶轮基本设计参数

1.2 仿鱼体结构提取与仿生叶片重构

关于鱼体外形结构特征的提取,本文采用文献[11]给出鱼体水平剖面的轮廓线方程

鱼体水平剖面轮廓线方程的x轴坐标范围为(-0.035 m,0.065 m),总长为0.1 m,鱼体水平剖面结构如图2所示。单圆弧叶片的弧长为17.4 mm,为了能应用于多翼离心风机叶轮中,首先需要对其进行比例缩小,使其中弧线长度和单圆弧叶片的中弧线弧长相同,且具有和单圆弧叶片中弧线同样的进出口安装角,然后将缩小的轮廓线离散为特征坐标点,再将特征点布置在中弧线两侧,通过样条拟合方法连接成一个封闭曲线,从而形成仿鱼形叶片轮廓结构。仿鱼形叶片与原始单圆弧叶片几何结构如图3所示。仿鱼形和原始单圆弧叶片均为对应截面轮廓结构直线拉伸而成的直叶片。

图2 鱼体水平剖面结构

图3 仿鱼形叶片与原始单圆弧叶片几何结构

1.3 计算模型、网格划分及网格无关性验证

计算模型主要由进口区、出口区、蜗壳区和叶轮区组成,根据物理模型的三维结构对流体区域进行建模,并通过ICEM CFD软件对计算模型进行网格划分。计算模型的进口向上游延伸了1.5倍集流器出口直径,出口向下游延伸了3倍风机出口水力直径。计算模型如图4所示。

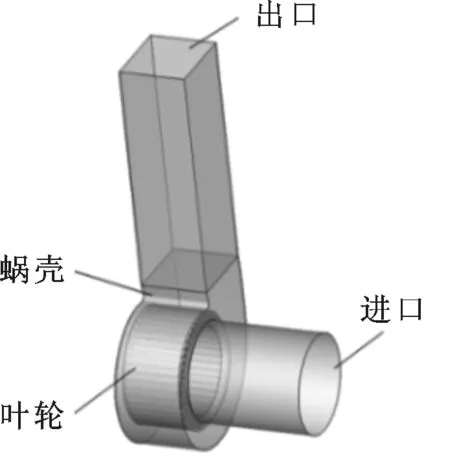
图4 多翼离心风机数值计算模型

首先通过验证网格无关性的方法来保证数值模拟的有效性和准确性,计算模型的网格数分别为94.5、144、200、237.7、356.6万。不同网格数对应的风量计算结果如图5所示,可知网格数超过144万时,风量的计算结果基本保持不变。为了数值计算的准确性和计算时间的合理性,计算网格定为237.7万。为了确保划分网格能反映风机内部流动状态及其复杂性,在近壁面进行了加密处理,并采用四面体和六面体的混合网格,其中蜗壳区域网格数为99万,叶轮区域网格数为92.7万,出口区域网格数为16.8万,进口区域网格数为29.2万。

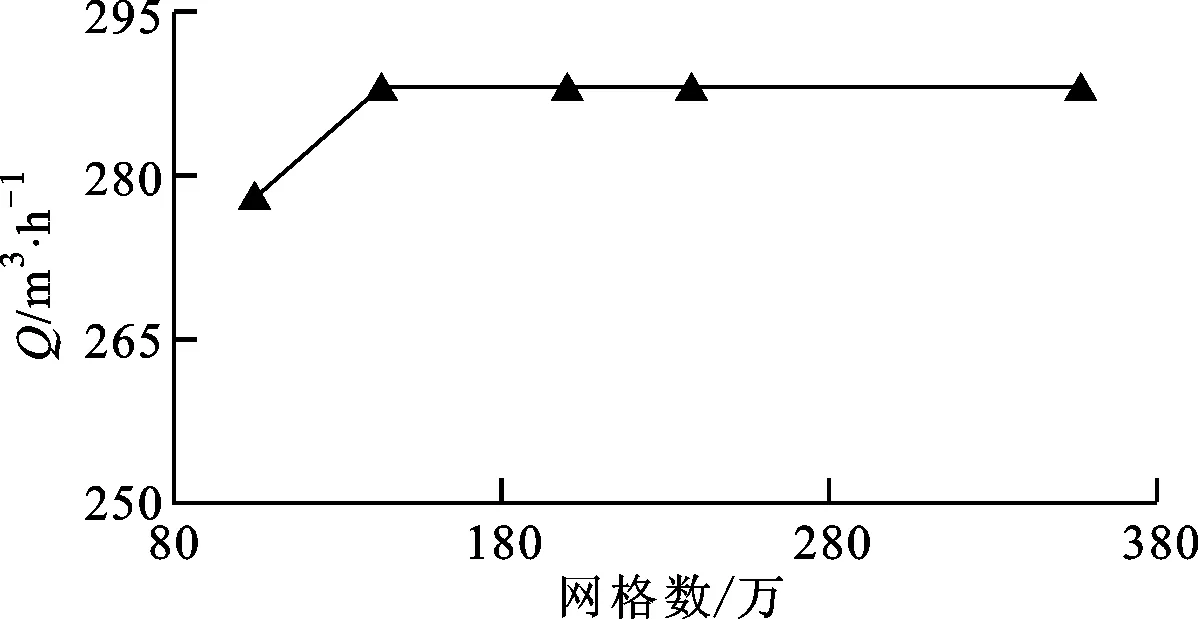
图5 网格无关性验证

在计算叶片式流体机械气动声学数值模拟中,为保证声学计算的准确性,单个网格单元要满足紧凑声源条件,即

Lmax<λmin/10

(1)

a=U/F

(2)

式中:Lmax为单个网格单元最大尺度,m;λ为声波波长,m;U为声速,m/s;F为关注频率,Hz。

至于内饰设计，全新航海家没有对MK X的设计做出调整，林肯标志性的按键式换挡与各功能按键依旧集成于操作台之上，12.3英寸的数字仪表盘可按车主需求调整显示内容。当然，如果中控台的8英寸触摸屏尺寸能再大一圈就好了，车载4G Wi-Fi功能、手机无线充电功能、Apple CarPlay则尽可能与智能手机做好搭档。

由于网格尺度和频率范围相互关联,选取声场计算范围为0～10 000 Hz,故λmin=34 mm,即Lmax<3.4 mm。本文所建立的蜗壳和叶轮区网格单元最大尺寸为2.5 mm,小于3.4 mm,满足紧凑声源条件,从而保证了声学计算的准确性。

1.4 原型风机风量测试结果

原型风机气动性能测试采用型号为FL-2 ISO的气动性能测试装置,测试装置原理为:从风机出来的气流被导向风室,测量静压后经过整流器,流向喷嘴。根据伯努利原理,利用流经喷嘴前后的压差可计算气流速度,用速度乘以喷嘴截面积即可求得风量。实验中利用辅助风机和调节挡板来改变风量,同时可以测量不同风量条件下对应的静压值,可得到出口相对静压为0时对应的风机最大风量,气动性能测试装置示意图如图6所示。气动性能实验测试和数值模拟的对比结果是:实验测试、数值计算流量为280、288 m3/h,绝对误差、相对误差为8、2.86%。对比风机的实验测量和数值计算结果,误差在工程允许的5%范围内,证明了本文计算方法的可靠性。

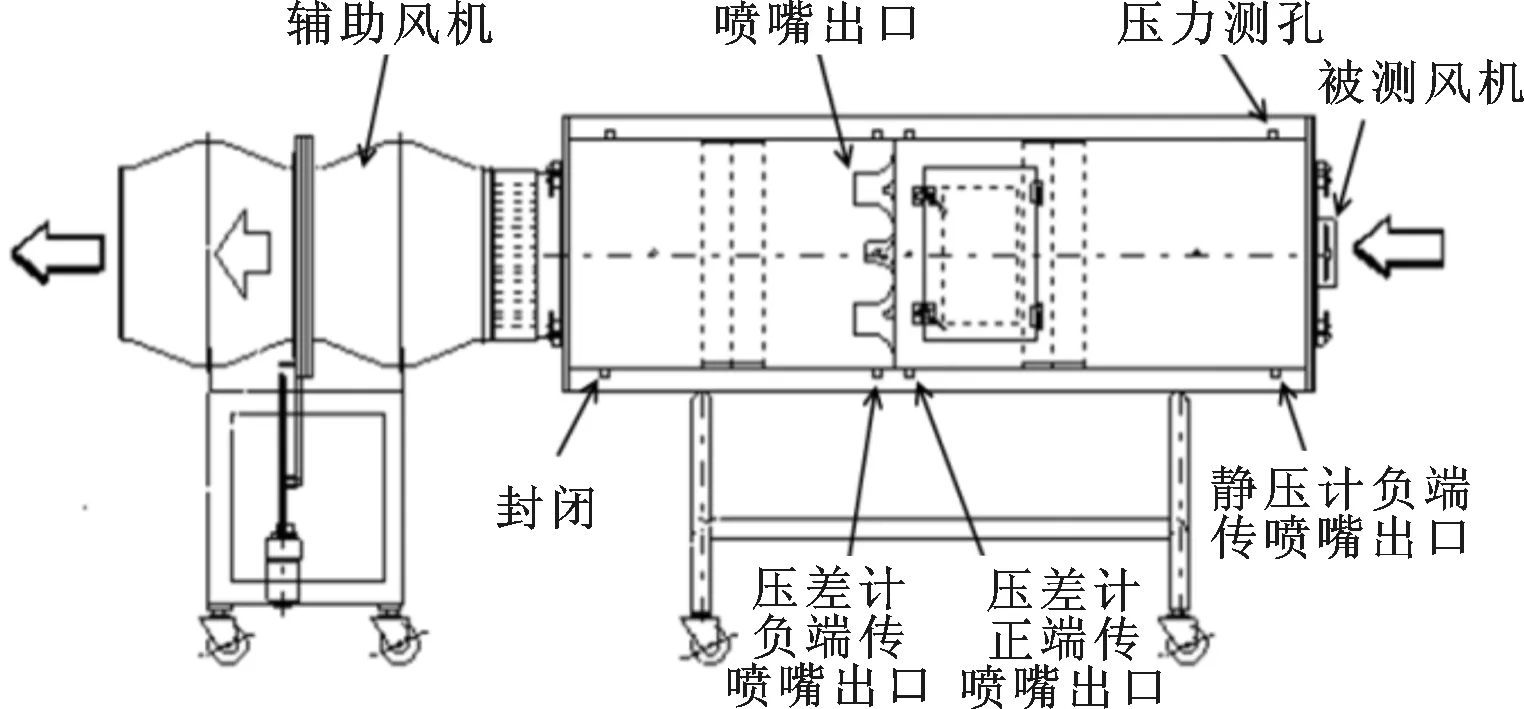
图6 气动性能测试装置示意图

2 数值结果及分析

2.1 定常计算

2.1.1 数值模拟方法及结果 采用CFD商用软件ANSYS Fluent 18.0对仿鱼形叶片风机和单圆弧原始风机进行数值计算。湍流计算采用Realizablek-ε模型[12-13],压力和速度耦合求解算法选用SIMPLE算法,压力离散格式选取PRESTO!格式。在流动控制方程的数值离散中,湍流耗散方程、能量方程和动量方程均设定为二阶迎风格式,计算收敛残差设定为10-4。进口给定总压边界条件,总压值为101 325 Pa,出口给定静压边界条件,静压值为101 325 Pa。进口区、出口区和蜗壳区设定为静止区域,叶轮区设定为旋转区域,旋转转速为1 100 r/min。原始风机、仿鱼形叶片风机的风量为288、324 m3/h,全压效率为37.89%、43.54%,可知当多翼离心风机采用仿鱼形叶片时,较采用单圆弧叶片的风机风量提高了12.5%,全压效率提高了5.65%,这说明将鱼体流线型轮廓结构用于多翼离心风机叶片设计是可行的,增风、增效方面可满足实际工程应用。

2.1.2 叶轮区流场分析 为了揭示叶轮区的流动状态,截取沿叶高中间面S2,沿S2平面向进口上移20 mm处的S1面以及沿S2面向远离进口下移20 mm处的S3面的叶轮流域平面,如图7所示。叶轮区速度流线如图8所示。

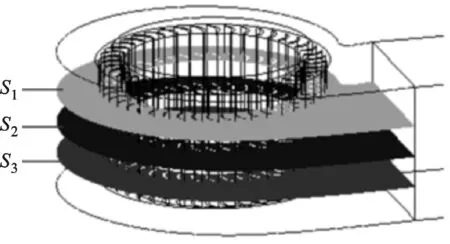
图7 计算模型观察面位置示意图

由图7可知:无论是仿生叶轮还是原型叶轮,在叶轮靠近蜗舌区域的旋涡强度均大于远离蜗舌流道内的区域,这说明蜗舌附近流道内的流动分离严重,叶轮和蜗壳之间有较强的相互作用,叶轮和蜗舌之间的相互作用造成蜗舌区的压力脉动是造成风机气动噪声较大的一个原因;同时,在S1、S2、S3这3个面内,仿生叶轮内部流道的旋涡强度均明显小于原型叶轮,流场更加均匀,有利于风机气动性能的改善;从S1、S2到S3面内,流道内的流动剧烈程度不断降低,这主要是由于风机为单面进气方式,在离进口较近的S1面内,流动较为剧烈,旋涡强度较小,叶轮和蜗舌之间的相互作用由于收到强气流的冲击作用而得到了削弱,使叶道内由于旋涡而造成的阻塞得到改善,气流流动更加顺畅,从而提高了风机的效率和流量,降低了叶轮区域所产生的涡流噪声,但随着离进口越远,这种冲击作用越来越弱,导致叶轮和蜗舌间的旋涡强度增大,仿生叶轮的这种冲击作用均优于原型叶轮,这说明仿生叶轮具有比原型叶轮更好的气动性能,同时缓解了叶道内的流动分离;由于鱼体表面的流线型结构,采用仿鱼形叶片使得气流从叶片前缘进入叶道后顺着鱼体轮廓表面向后流动,实现了沿叶片表面较好的流速分布,改善了叶片表面的附面层的分离和发展,从而降低了叶道内的气流阻力和涡流噪声。

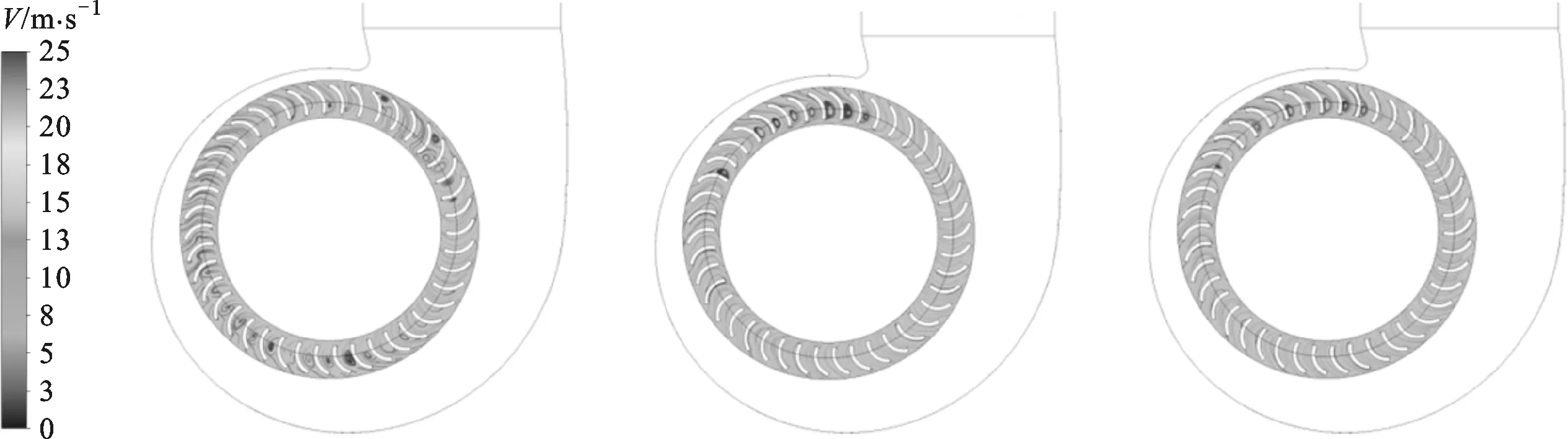
(a)单圆弧叶片叶轮区S1、S2和S3的速度流线图

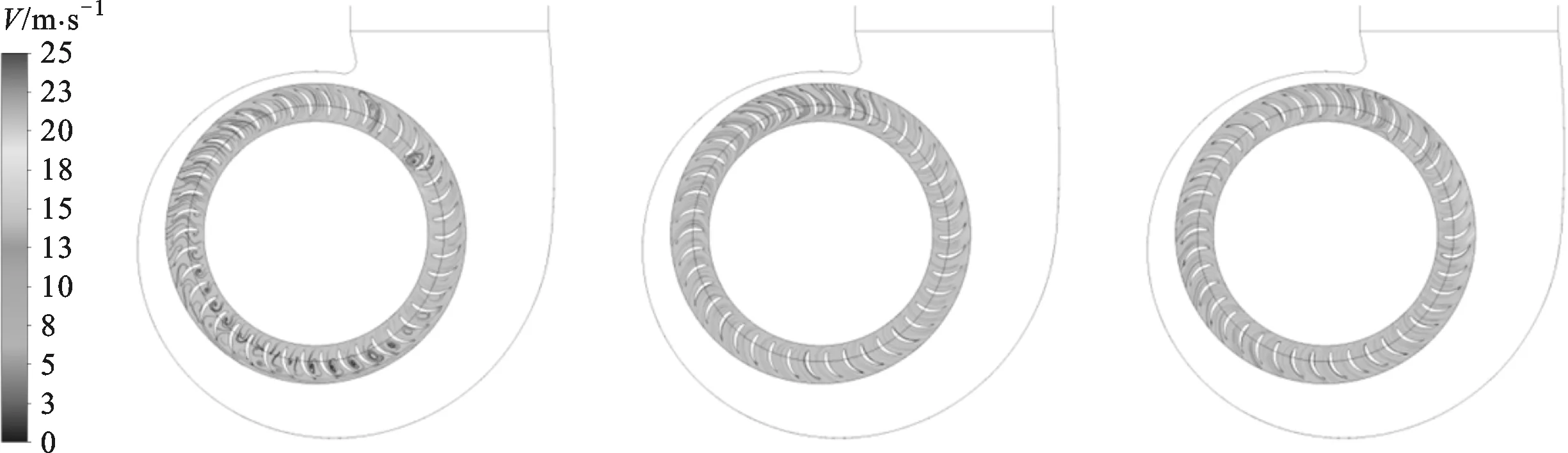
(b)仿鱼形叶片叶轮区S1、S2和S3面的速度流线图图8 叶轮区速度流线图

2.2 非定常计算

以定常计算收敛后的计算结果作为非定常计算的初始值,时间项设定为二阶隐式格式,叶轮区改用Mesh Motion模型,时间步长Δt为5.05×10-5s,叶轮旋转5周,当监控变量的变化呈周期性时,表明风机处于稳定工作状态。

2.2.1 叶轮区涡量分析 叶轮区涡量分布如图9所示,可知仿生叶轮和原型叶轮的涡脱落区域主要集中在远离进口区的区域,旋涡强度最大值区域分布在叶轮靠近蜗舌的区域,这主要是由叶轮和蜗舌相互作用造成的。由图9可知,仿生叶轮的最大值区域面积小于原型叶轮的,从整个叶轮区域的涡分布情况来看,仿生叶轮的涡脱落分布情况优于原型叶轮的,这验证了仿生叶轮比原型较好地缓解了叶道内流动分离的结论。根据涡声理论,气动噪声与涡量的大小有直接联系[14],可知叶轮和蜗舌区域是风机噪声的主要来源,因此改善叶轮和蜗舌区域的流动状况是降低风机涡流噪声的关键。仿生叶轮区域的流动状况优于原型叶轮的,这说明仿生叶轮区域的涡流噪声要小于原型叶轮区域的。

(a)仿鱼形叶片叶轮区 (b)单圆弧叶片叶轮区图9 叶轮区涡量分布图

2.3 噪声计算

2.3.1 噪声计算 非定常流动计算稳定后,作为FW-H声学方程的输入项,设置叶轮和蜗壳为噪声源,并设置噪声接收点,再进行叶轮旋转5周的气动噪声计算。在设置噪声接收点时,按照GB/T 4214.1 —2000中通风器具规定的测试点设置噪声接收点,基准体的每一边长不超过0.7 m,测量表面为半球面,带有10个测点,测点分布情况如图10所示,半球面测量表面的半径r设定为1.5 m。监测点1～10的位置坐标为(0,1.485 m,0.039 m)、(0,-0.743 m,1.325 m)、(0,-0.743 m,-1.247 m)、(0.45 m,0.671 m,1.201 m)、(0.45 m,0.671 m,-1.123 m)、(0.45 m,-1.342 m,0.039 m)、(0.9 m,0.995 m,0.039 m)、(0.9 m,-0.498 m,0.901 m)、(0.9 m,-0.498 m,-0.823 m)、(1.277 m,0,0.039 m)。

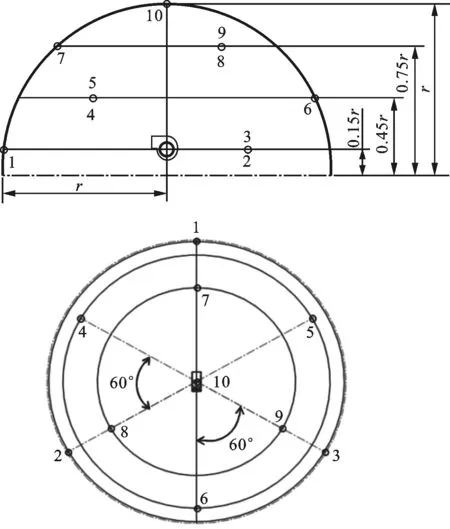
图10 噪声计算监测点布置图

通过计算声场,获得按照上述位置布置的10个点的声压级噪声值,如表2所示。由表2可知,每个点的声压级均不同,表明多翼离心风机的噪声声场并不是沿半球面均匀分布的,而是具有一定规律的指向性,原型风机的最大声压级为37.38 dB,在3点,4点声压级值紧随其后,这说明原型风机的噪声向两侧传递的噪声强度大于出口方向,而仿鱼形叶片风机在1点的声压级最大,为34.8 dB,其他各点均和1点差距1 dB以上,说明仿鱼形叶片风机在出口方向具有较大的噪声强度。这两类风机噪声监测点的均值分别为35.73、32.95 dB,相差2.78 dB,说明仿鱼形叶片具有较好的降噪效果。

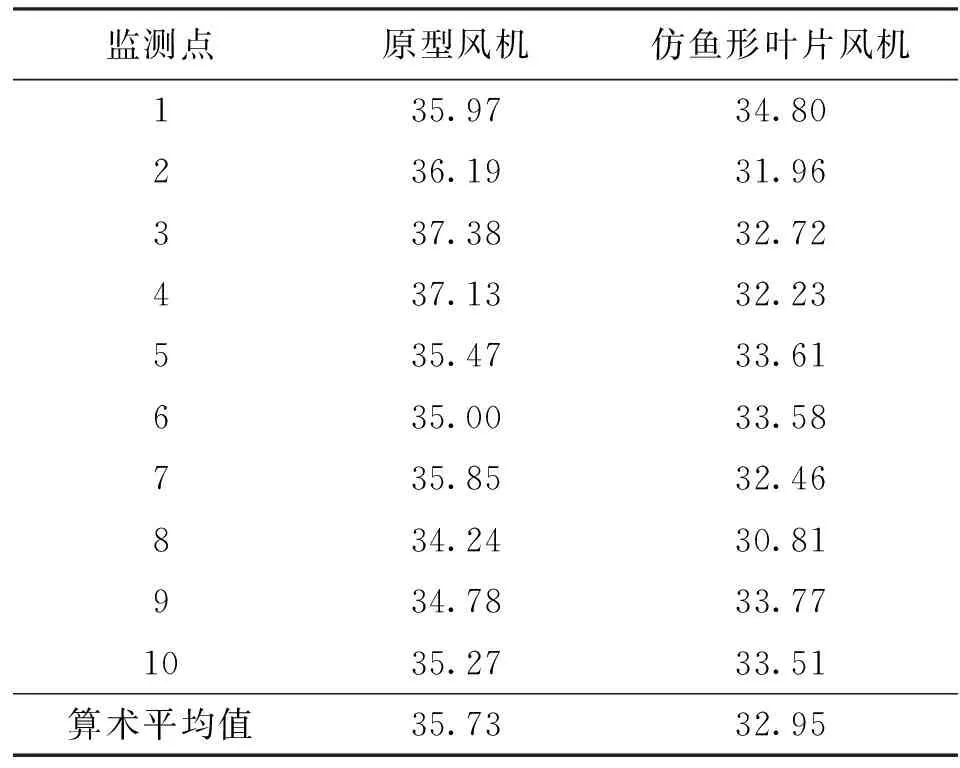
表2 两种风机模型监测点处声压级 dB

声场计算完成后,通过傅里叶变换可得到噪声频谱图,其中叶片频率的计算式为

(3)

式中I为谐波序号(I=1时为基频)。计算可得风机基频为660 Hz。本文选取两种风机的噪声最大值点进行对比分析,分别为1点和3点,这两种风机在1、3点的噪声频谱如图11所示。由图11可知,噪声随频率呈周期性变化,在频率为660 Hz处出现峰值,这与式(3)计算的风机基频相同,验证了噪声模拟计算的正确性。

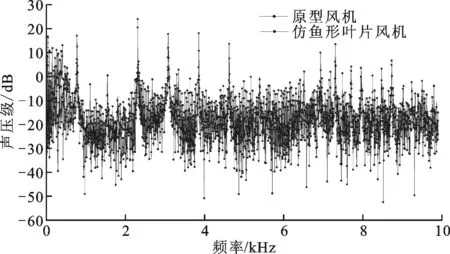
(a)两种型式风机在1点的噪声频谱图

(b)两种型式风机在3点的噪声频谱图图11 两种型式风机在1点和3点的噪声频谱图

对于1点,原型风机和仿鱼形叶片风机的噪声最大值点分布规律相同,均在230 9 Hz处声压级达到最大,即原型风机起决定作用的声压级最大值为23.9 dB,仿鱼形叶片风机起决定作用的声压级最大值为20.4 dB,小于原型叶片的最大声压级;对于3点,原型风机在频率为230 9 Hz处声压级达到最大值27.6 dB,仿鱼形叶片风机的最大值为17.8 dB,小于原型风机的最大声压级,但在3点,仿鱼形叶片风机和原型风机并不是在同一频率点取得最大值。从0～10 000 Hz的噪声声压级分布情况可知,对于原型风机1点和3点,在小于500 Hz的低频声段均存在较高的声压级,而在500～10 000 Hz中频声段,呈现明显的周期性变化,但均存在几个峰值,这说明对于原型风机,噪声在低频声段和中频声段都有分布;对于仿鱼形叶片风机,在0～10 000 Hz频率范围内表现为周期性变化,同样存在几个峰值,但在低频声段具有较低的声压级,主要集中在中频声段范围内,这说明原型风机和仿鱼形叶片风机噪声频率分布规律不一致。由于不同声段噪声的传播特性不同,所以原型风机和仿鱼形叶片风机在半球面10个测点的声压级分布规律不同。

原型风机与仿鱼形叶片风机1点和3点的声压级1/3倍频程频谱如图12所示。对于1点,在0～630 Hz范围内,原型风机声压级明显高于仿鱼形叶片风机,这说明在低频声段原型风机对噪声有重要的贡献,而且原型风机和仿鱼形叶片风机噪声频率分布规律不同;在2 000～2 500 Hz范围内,原型风机声压级达到最大值33.43 dB,而仿鱼形叶片风机在2 500～3 150 Hz范围内,声压级达到最大值30.07 dB,低于原型风机声压级的最大值;在630～800 Hz和2 500～6 300 Hz范围内,仿鱼形叶片风机的声压级大于原型风机,其他频率段均低于原型风机,但仿鱼形叶片风机起支配作用的声压级仍小于原型风机。

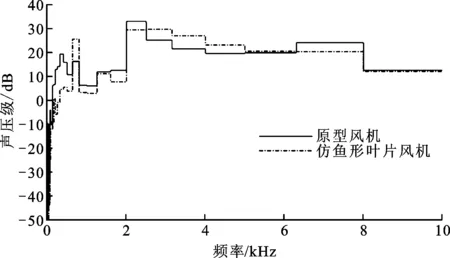
(a)两种风机在1点的声压级1/3倍频程频谱图

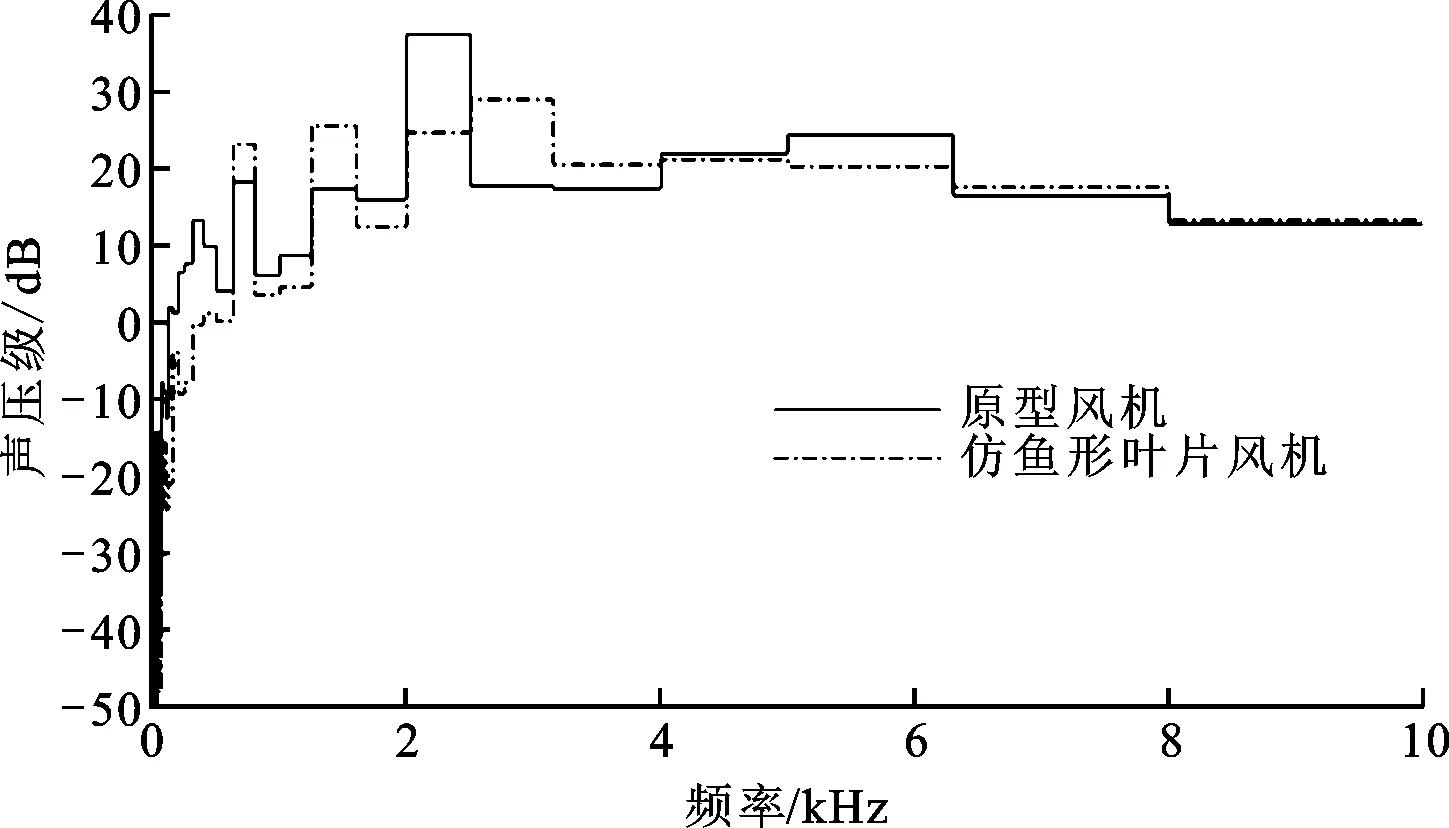
(b)两种风机在3点的声压级1/3倍频程频谱图图12 两种多翼离心风机在1点和3点的声压级1/3倍频程频谱图

对于3点,在0～630 Hz范围内,原型风机声压级高于仿鱼形叶片风机,这和1点的规律一致;在2 000～2 500 Hz范围内,原型风机声压级达到最大值,为37.63 dB,仿鱼形叶片风机在2 500～3 150 Hz范围内,声压级达到最大值,为29.1 dB,低于原型风机声压级的最大值;同样,在630～800 Hz、1 250～1 600 Hz、2 500～4 000 Hz和6 300～10 000 Hz范围内,仿鱼形叶片风机的声压级大于原型风机的,其他频率段均低于原型风机,但仿鱼形叶片风机起支配作用的声压级小于原型风机的。

2.3.2 蜗舌区域的声压脉动时均值分析 仿鱼形叶片风机和原型风机蜗舌区域表面局部声压脉动时均值Q分布如图13所示。由图13可知,仿鱼形叶片风机蜗舌区域的声源区域面积小于原型风机蜗舌区域,说明采用仿鱼形叶片可有效降低蜗舌部位处的声压脉动,减弱叶片与蜗舌之间的非定常相互作用,从而降低多翼离心风机的气动噪声。

(a)仿鱼形叶片蜗舌区域 (b)单圆弧叶片蜗舌区域图13 蜗舌区域压力脉动

从流场涡量分布图、蜗舌区域压力脉动图和噪声计算分析可知,尽管仿鱼形叶片和单圆弧等厚叶片具有相同的中弧线特征,但仿鱼形叶片具有与单圆弧等厚叶片不同的叶片型线和尾缘结构,在尾缘形成的尾流射流角度相对于单圆弧等厚叶片发生了偏转,仿鱼形叶片降低了尾流射流对蜗舌和蜗壳其他区域的冲击强度,减弱了叶片尾缘的“尾流-射流”效应,改善了尾流和蜗舌区域以及蜗壳其他部分的相互耦合作用,从而降低了仿鱼形叶片风机蜗壳内部的气流沿程阻力,提高了风机的气动性能,从根本上改善了蜗舌和蜗壳其他区域内的声压脉动强度,从而有效降低了风机的气动噪声。

3 结 论

基于鲹科鱼类机动游动姿态和涡流特征,对通风换气装置用多翼离心风机叶片进行了仿生重构设计,采用数值方法研究了单圆弧原型叶片和仿鱼形叶片对多翼离心风机气动性能和噪声的影响。获得的主要结论如下。

(1)仿鱼形叶片风机与单圆弧原型叶片风机相比,风量增大了36 m3/h,效率提高了5.65%,表明将鱼体流线型轮廓结构和弯曲姿态用于多翼离心风机叶片设计是有效的。从增风增效的角度来看,仿鱼形叶片设计可满足实际产品应用的要求。

(2)通过对两种类型风机进行的噪声计算可知,对于原型风机,噪声在低频声段和中频声段都有分布,而仿鱼形叶片风机噪声主要集中在中频声段范围内,这说明原型风机和仿鱼形叶片风机噪声频率分布规律不相同,采用仿鱼形叶片的多翼离心风机在测点处噪声平均值降低了2.78 dB。

(3)由于鱼体表面具有流线型结构,采用仿鱼形叶片实现了沿叶片表面较好的流速分布,改善了叶片表面的附面层的分离和发展,从而降低了叶道内的气流阻力,改善了叶道内的涡流噪声。同时,仿鱼形叶片在尾缘形成的尾流射流降低了对蜗舌和蜗壳的冲击强度,改善了蜗舌和蜗壳表面的声压脉动强度,有效降低了风机的气动噪声。