3UPS-RPR并联机构的静力学分析

冯志友，倪迎真，贠今天

（天津工业大学天津市现代机电装备技术重点实验室，天津300387）

3UPS-RPR并联机构中3条UPS支链为无约束支链，RPR支链自由度与该机构的自由度相同，为恰约束支链，且RPR支链为摆动支链，有广阔的工作空间.由于约束的存在限制了机构部分自由度，少自由度并联机构的研究更为繁琐.该种机构自由度的确定[1]、奇异性分析[2-4]、运动学性能评价[5]均需要建立完整的雅可比矩阵.完整雅可比矩阵作为连接输入与输出的桥梁，以完整雅可比矩阵为基础构造出的性能指标反映了机构的运动或力传递的灵敏度.在对机构静力学性能的分析中，基于完整雅可比矩阵构造出来的力传递性能指标也是衡量并联机构工作性能优劣的重要指标[6].曲海波等[7]通过求解出各个分支的力反螺旋对4RRS并联机构静力学进行研究；路光达等[8]运用支链方向向量法建立静力学模型，对3RSS-S并联机构进行了实验探究；王中林等[9]在静力平衡方程的基础上运用小变量协调方程求解出力之间的映射关系；Huber等[10]将静力学研究引入到了机构的奇异性问题；艾青林等[11]从不同类型机构包括杆支撑、绳牵引和钢带传动形式等方面概括了国内外并联机构静力学分析的进展程度；邓昱等[12]针对少自由度并联机构进行了静力学分析；Ninomiya等[13]对并联谐振转换器进行了动力学和静力学特性分析.由于3UPS-RPR并联机构中间是一条RPR摆动支链，工作空间/机构体积参数大，应用在并联机床领域可以大大缩小机床体积.本文在完整雅可比矩阵的基础上，借助功能原理，构造了静力学力传递性能指标，分析了部分结构参数及末端位姿变化对传力性能的影响规律.

1 机构描述

3UPS-RPR并联机构结构简图如图1所示.

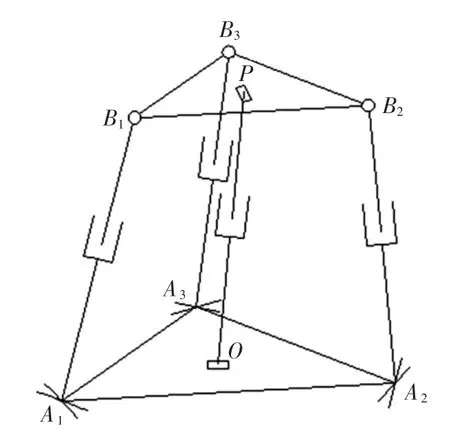
图1 3UPS-RPR并联机构结构简图Fig.1 Schematic diagram of 3UPS-RPR parallel mechanism

由图1可见，3UPS-RPR并联机构是由动平台（上）、静平台（下）、3条无约束驱动支链（UPS）和1条恰约束从动支链（RPR）构成.其中，U、P、S分别表示虎克铰、移动副和球面副.该机构中的3个移动副（P）为该机构的驱动副.UPS支链的一端通过虎克铰与静平台连接，另一端则通过球面副与动平台相连；RPR支链的两端分别通过转动副与静、动平台连接，支链中间运动副为移动副，移动副前段定长连杆为l，且两转动副轴线互相垂直，分别位于静、动平台的中心.该机构通过3个移动副的输入实现1平动2转动（1T+2R）3个自由度.设定由点Ai构成的静平台为等边三角形，该三角形的中心为O，其外接圆半径为a，同样由点Bi构成的动平台也为等边三角形，该三角形的中心为P，其外接圆半径为b.

1.1 建立坐标系

初始位置时坐标系建立如图2所示.建立固定坐标系O-xyz，其中x轴与y轴的建立如图2（a）所示，z轴垂直于静平台；建立动坐标系P-uvw，其中v轴与RPR支链与动平台连接处转动轴线重合，u轴与边B1B2平行，如图2（b）所示，w轴符合右手定则.

动平台相对于定坐标系的姿态可通过先绕x轴旋转α角，再绕旋转后的v轴旋转β角实现.则旋转矩阵可表示为：

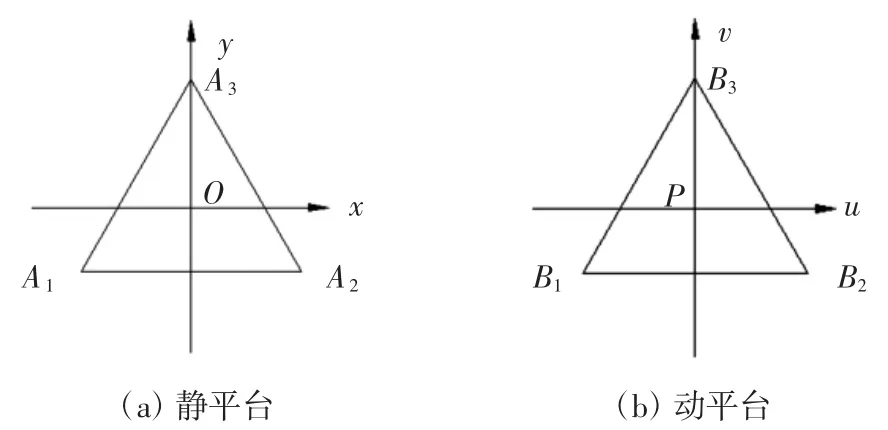
图2 静、动平台在各自坐标系中的位置关系Fig.2 Position relationship of static and dynamic platform in their coordinate system

旋转矩阵中各列向量分别为动系各坐标轴矢量.

1.2 位置逆解模型

假设已知动平台末端位姿参数α、β、q4后，即可求得对应的各个输入参数q1、q2、q3的具体数值.

动平台上P点位置矢量r=（xpypzp）T，有

在定坐标系O-xyz下根据闭环矢量[14-15]可以建立如下约束方程

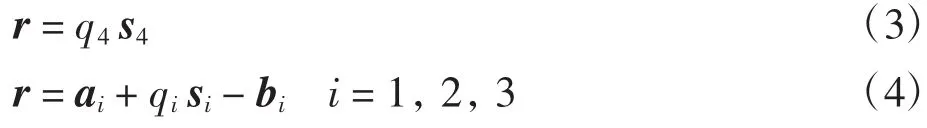
式中：s4为向量r的单位矢量；qi、si分别为第i条UPS支链的长度和AiBi方向的单位矢量；ai、bi分别为矢量OAi、PBi在定坐标系O-xyz中的表示.其中

式中：bPi为PBi在动坐标系P-uvw下的矢量.

已知：

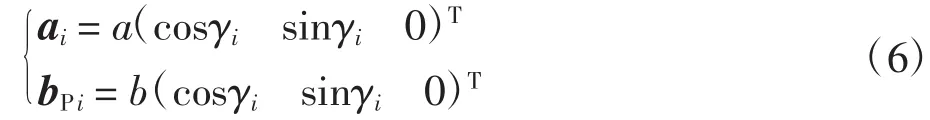
式（6）中：γi=（4i-9）π/6，i=1，2，3

联立式（1）、（3）、（4）、（5），可求得机构的输入：

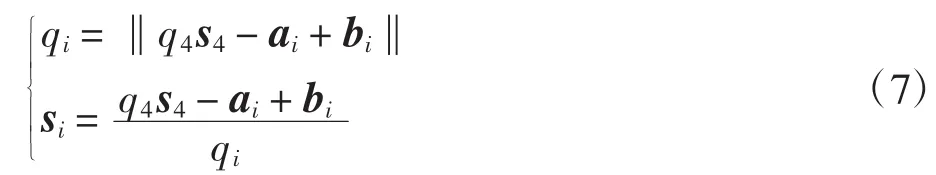
1.3 机构逆位置仿真计算

由于上述结果为后续研究的基础，必须确保其正确性，对运动学研究结果进行仿真验证.设定3UPS-RPR并联机构几何参数如下：a=1 m，b=0.6 m，l=0.25 m.给定机构末端的运动参数为

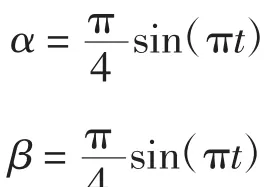
运动过程中，设定RPR支链运动时的变化规律为

已知机构位置逆解模型，把机构末端输出规律代入到3UPS-RPR并联机构位置逆解模型中，就能得到各个UPS驱动支链总长qi（i=1，2，3）变化规律即输入变化规律，如图3所示.

图3 UPS支链总长qi曲线Fig.3 Graph of UPS branch length qi

在给定机构末端位姿的情况下，得出各个UPS驱动支链总长qi（i=1，2，3）在一个周期内的变化规律，验证了求解结果的正确性.

2 完整雅可比矩阵

动平台的瞬时运动螺旋可以表示为

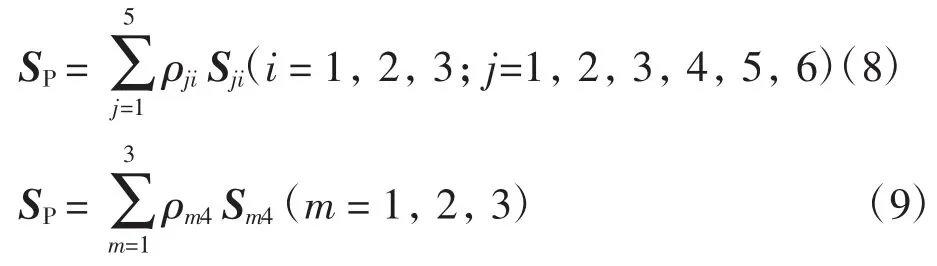
式中：Sji为支链i中第j个单自由度副的瞬时运动螺旋；ρji为支链i中第j个单自由度副的速率；ρm4为支链RPR中第m个单自由度副的速率；Sm4为支链RPR中第m个单自由度副的运动螺旋.

2.1 约束子雅可比矩阵

仅对恰约束支链进行研究，建立支链RPR运动螺旋

根据反螺旋方法，可得式（10）一个反螺旋

根据互易积[16]，得

将式（11）整理成矩阵形式，有

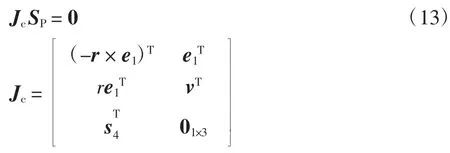
由于 e1、r、v向量两两垂直，且有e1=x，则

式中：Jc为3UPS-RPR并联机构的约束子雅可比矩阵.

2.2 驱动子雅可比矩阵

该机构中支链UPS是无约束驱动支链，支链中P为驱动副，则运动螺旋表示如下

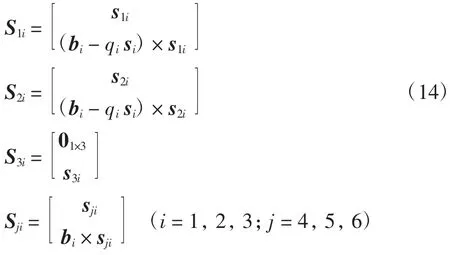
锁定UPS支链的主动关节，即移动关节.每个UPS支链将会变为US支链，其瞬时运动螺旋为

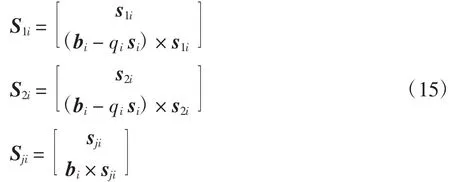
由于被动关节从物理层面讲瞬时功率为零，驱动力（偶）表示为与所有被动关节的互易积都为零的反螺旋，为

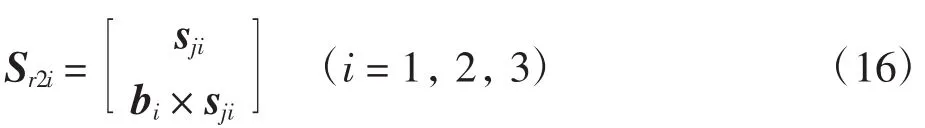
式（8）与式（16）做互易积，可得：

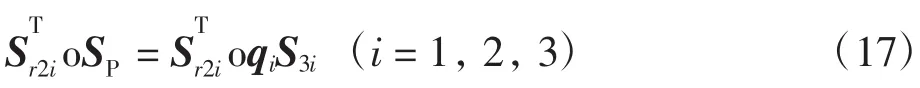
可知：

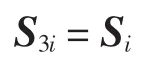
则有

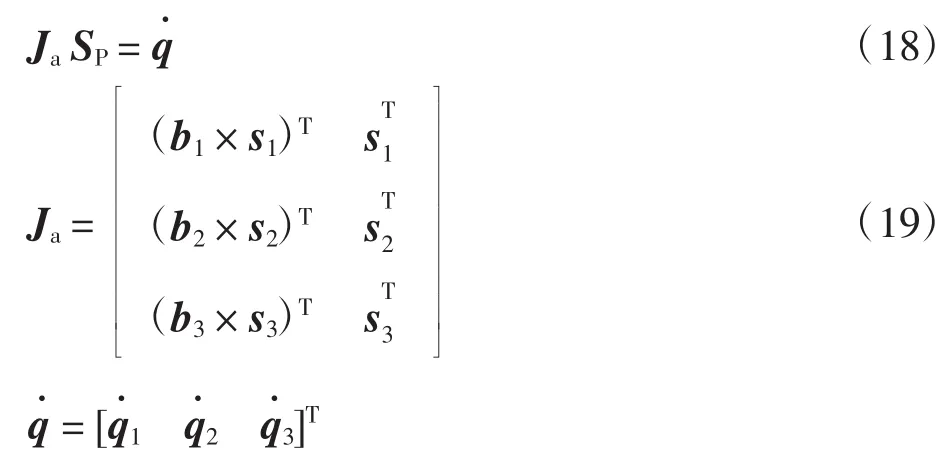
式（19）中Ja为驱动子雅可比矩阵.

联立式（13）和式（18）可得

3 静力学分析

由虚功原理得：

即驱动力所作虚功与机构末端广义力所作虚功相等.

将式（22）整理成矩阵形式

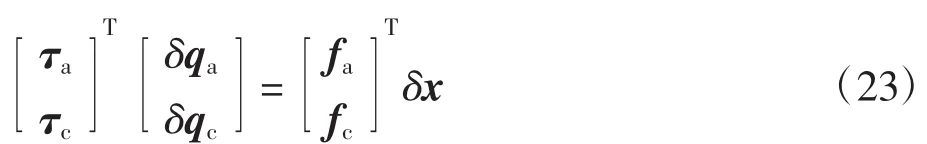
式（23）可以分解成如下形式的2个子式，如式（24）、（25）所示：

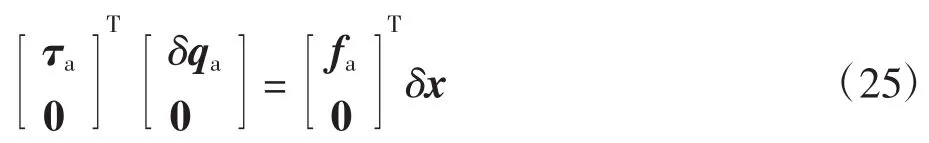
类比于输入与输出速度之间映射关系，两边对速度积分，可得如下形式方程式

将式（26）、（27）分别代入式（25）、（24），整理可以得到

根据式（28），设定kJa、kJc为驱动矩阵条件数、约束矩阵条件数

选取 kJa、kJc的全域平均值 ζkJa、ζkJс作为评价机构力传递性能的指标

因为 ζkJa、ζkJс大于1，越接近于 1 机构的力传递越灵敏.

给定机构几何参数，a=1 m，b=0.6 m，l=0.25 m，由式（30）计算kJa、kJc的全域性能指标，可以分析3UPS-RPR并联机构的力传递性能与机构结构参数（静动平台半径比λ=a/b、定长连杆l）间关系，如图4—图7所示.

图4—图5给出了机构的力传递性能随静动平台半径比的响应曲线.由图4可以看出，当λ在0.3～0.9区间内，机构约束力传递性能评价指标随λ的增大而减小，λ大于0.9时，机构的约束力传递性能趋于平稳.由图5可以看出，当λ大于3，机构驱动力传递性能较好且稳定.综上所述，λ的参数设计范围选择在3～5之间.

图4 机构约束力传递性能与λ的关系Fig.4 Relationship between mechanism binding transfer performance and λ

图5 机构驱动力传递性能与λ的关系Fig.5 Relationship between mechanism driving transfer performance and λ

图6 机构约束力传递性能与l的关系Fig.6 Relationship between mechanism binding transfer performance and l

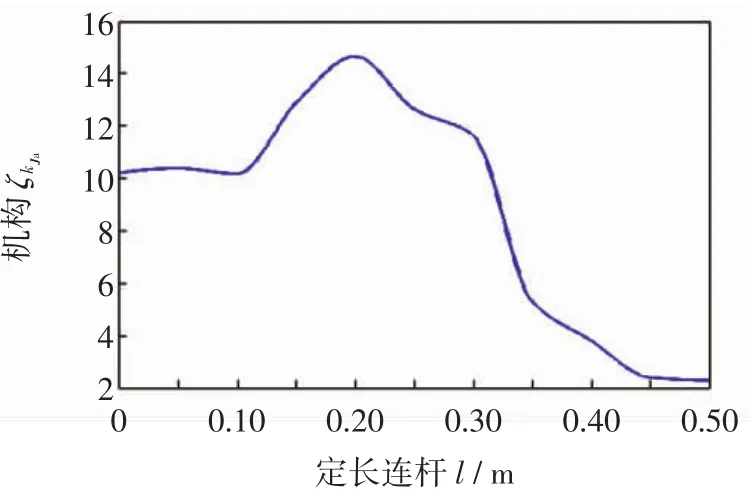
图7 机构驱动力传递性能与l的关系Fig.7 Relationship between mechanism driving transfer performance and l

图6—图7给出了机构的力传递性能随杆l长度变化的规律.由图6可以看出，当l处于0～0.23范围内时，机构的约束力性能评价指标随l的不断增长呈现出先减小后增大再减小的变化规律，当l长度大于0.18时，比较平稳，机构的约束力传递性能较好.由图7可以看出，机构的驱动力传递性能评价指标在一定范围内随l的增大先增大后减小的变化规律.综上所述，l的参数设计范围选择在0.3～0.45之间.

图8显示了机构的约束力传递性能与运动过程中恰约束支链所处位置之间的关系，当RPR支链摆角处于相对较小范围内时约束力传递性能较好，随着摆角增大，约束力传递性能降低.

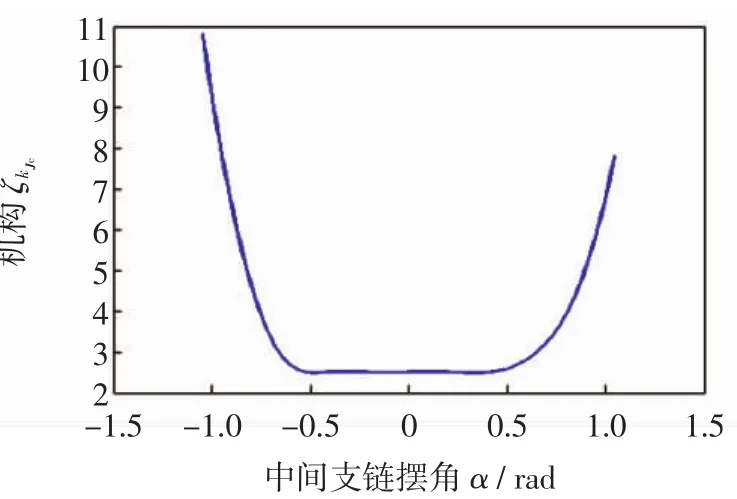
图8 机构约束力传递性能与α的关系Fig.8 Relationship between mechanism binding transfer performance and α

4 结论

（1）利用空间闭环矢量法建立了3UPS-RPR并联机构的逆位置模型，得到逆位置解.在逆解基础上借助螺旋理论，用反螺旋方法求得机构的完整雅可比矩阵.

（2）借助虚功原理思想，基于6×6阶完整雅可比矩阵分别求得驱动力和约束力输入与输出间的力雅可比矩阵，建立了全域范围内的力传递性能指标.

（3）分析了机构拓扑构型参数对力传递性能的影响，得到了机构设计过程中并联机构优选的静动平台半径比λ在3～5之间，中间摆杆运动范围为-0.5～0.5 rad.实际应用中，在高性能结构参数的基础上可以通过调节末端位姿范围来进一步提高机构的性能.