具有2T1R与2R1T运动模式3自由度并联机构型综合

刘 伟 刘宏昭

(1.西安理工大学机械与精密仪器工程学院，西安 710048; 2.西安工程大学机电工程学院，西安 710048)

0 引言

近些年关于并联机构的型综合研究主要集中在通过并联机构型综合，降低机构的耦合来提升并联机构运动性能和可控性[1]，增大机构的耦合来提升机构刚度[2]，提升并联机构的可重构性以适应不同的工作需要[3]。

具有2T1R运动模式的并联机构在工业装配机器人、姿态调节器、并联机床、工作台等领域应用比较广泛[4-5]。具有2R1T运动模式的并联机构，适合应用于在曲面上工作的操作手，具有刚度高、精确度高、灵巧性强等特点[6]。文献[7]对2R并联机构进行了运动解耦方面的设计。文献[8]对2R2T完全解耦的并联机构进行了综合。具有多种运动模式的并联机构使用较少的驱动可实现多种运动模式，以较少的成本可以提升机器适应实际工业生产中多样的需求。具有多种运动模式的并联机构，也称为具有多种操作模式、位移子群可变、具有运动分岔或者可重构并联机构。其特征为：较少的驱动副可以实现多种运动模式；运动模式变换时不需要对机构进行重新组装，因而可以快速实现机构重构；一些此类并联机构在进行运动模式变换时，需要通过机构的奇异位形[9]。DYMO并联机构具有4种不同的3自由度运动模式[10]。文献[11]使用虚拟运动链，先对不同运动模式的并联机构支链进行型综合，选择两种运动模式共有的支链结构作为可选支链，再结合不同运动模式支链装配的几何条件，综合了具有多种运动模式的并联机构。文献[12]使用具有多种运动模式的单环机构综合了可实现3R2T与2R3T[13]两种运动模式相互转变的并联机构。文献[14]综合了实现3T、3R、2R1T、2T1R三自由度运动模式相互转换的并联机构。这些并联机构可以实现多种运动模式变换，绝大多数需要使用含有多个驱动副的单环机构。文献[15]基于方位特征集，使用可变自由度支链、定自由度支链、六自由度支链综合了具有两转两平移和一转三平移的并联机构[16]。

然而，目前实现2T1R与2R1T运动模式转变的并联机构较少，本文使用位移流形理论对此类型的并联机构进行综合。

1 分支运动链综合

使用Oxyz表示笛卡尔坐标系，其原点为O，正交基为(x，y，z)。使用(A，z)表示通过空间中一点A，方向平行于z的直线，结合运动副类型表示运动副的方向和运动副轴线上的点。平行于z轴过点N的转动副对应的位移子群用{R(N,z)}表示。平行于轴线z的转动副表示为zR。一条串联运动链由构件1，2，…，i-1，i组成。构件i的可允许的位移可以表示为运动链中运动副所表示的位移子群的乘积。一个构件通过zRzRzR运动链与定平台相连，这个运动链产生一个平面3维位移子群{G(z)}。如果运动链产生的相对于定平台的运动不具有群的结构，就称其产生一个位移流形。

{G(z)}表示平面位移子群，z表示平面位移运动所在平面的法线方向。{G(z)}可以被分解成为7种乘积形式[17],即

{G(z)}={T1(x)}{T1(y)}{R(N,z)}=
{R(N,z)}{T1(x)}{T1(y)}=
{T1(x)}{R(N,z)}{T1(y)}=
{R(A,z)}{R(B,z)}{T1(y)}=
{R(A,z)}{T1(y)}{R(B,z)}=
{T1(y)}{R(A,z)}{R(B,z)}=
{R(A,z)}{R(B,z)}{R(C,z)}

(1)

{G(z)}具有7种等效运动链。它们是xPyPzR、zRxPyP、xPzRyP、zRzRxP、zRxPzR、xPzRzR和zRzRzR。

1.1 构造定自由度运动链

HERVE[18]给出了位移子群两两求交以及乘法运算的运算结果，并指出位移子群求交集的运算满足一般集合论中的求交法则。而在更多情况下由运动链(多个运动副组合而成)生成的刚体运动并不能满足位移群的代数结构，而只是其中的位移子流形。

运动副和运动链可直接作为位移子群或位移子流形的生成元(或生成算子)；相应地，运动链末端相对于固定端的任一运动，无论其多么复杂，都可以表示成若干位移子群或位移子流形以及它们之间的乘积形式。通常情况下，运动链末端的运动可由运动链中所有低副生成的位移子群的乘积来决定。这些位移子群的乘积可能仍然是位移子群，但在大多数情况下这个乘积不具有群的代数结构，只是一个位移子流形。

M=M1‖…Mk表示由k条串联的运动链M1，M2，…，Mk组成的并联机构，它们都与共同的动平台和定平台相连接。用符号C表示机构末端的运动，则并联机构动平台的运动可表示为

CM：=CM1∩CM2∩…∩CMk

(2)

由式(2)可知，动平台的运动应该是并联机构支链运动的交集。

定理1：任意位移子群的乘积运动A·B可能构成位移子群，也可能不具有群的代数结构，只是一个位移子流形。一般情况下不满足交换律，即A·B≠B·A。但是如果满足交换律A·B=B·A，则A·B也是位移子群[19]。

由于并联机构的动平台运动模式需从2T1R向2R1T转变，根据式(2)的求交运算可知，并联机构的分支运动链，应至少可以实现2R2T的运动。2T1R是平面位移子群{G(z)}。{R(x)}是一维转动子群。2R2T不属于HERVE[18]枚举出的刚体运动中存在的全部12种位移子群。因而，根据定理1可知2R2T是位移流形。具有2R2T位移流形的支链，可以通过对具有2T1R平面位移子群的支链进行等效替代得到：xPyPzRxR、zRxPyPxR、xPzRyPxR、zRzRxPxR、zRxPzRxR、xPzRzRxR、zRzRzRxR。

由于6自由度支链不给动平台施加约束，因而也可用来实现2R1T运动模式向2T1R运动模式转变的并联机构的构造。GOGU[20]使用进化形态理论，对6自由度分支运动链进行了综合，具体运动链结构如表1所示，表1中22～24号支链中存在局部自由度，表1中其他的运动链中不存在局部自由度。除了表1中的运动链以外，还有一些运动链中含有与2个以上构件相连的构件，即复杂运动链，也具有6自由度。

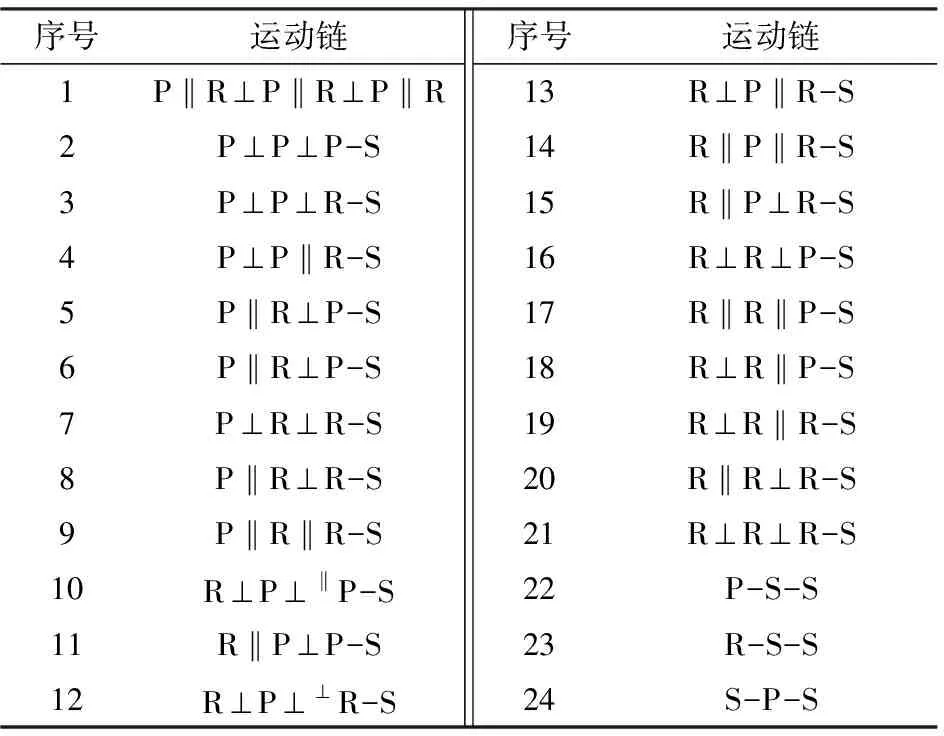
表1 6自由度支链等效运动链Tab.1 Equivalent kinematic chain of fixed six degrees of freedom branches kinematic chain

1.2 基于位移流形理论选取变自由度分支运动链

一般情况下，并联机构支链结构可以根据位移子群或位移流形的生成元得到。定自由度支链位移流形为

{R(O,z)}{T1(x)}{T1(y)}{R(N,x)}

(3)

根据动平台具有的运动模式，构造变自由度运动链生成元为

{R(O,z)}{T1(x)}{T1(y)}{R(N,x)}∩

({R(A,z)}{T1(x)}{T1(z)}{R(C,y)}{R(B,z)}∪
{R(A,z)}{T1(y)}{T1(z)}{R(C,x)}{R(B,z)})

(4)

由于{R(O,z)}{T1(x)}{T1(y)}、{T1(y)}{T1(z)}{R(C,x)}平面位移子群在位移流形求交时，转动副R所过的点在xoy、yoz平面可任意选取，得到

{R(A,z)}{T1(x)}{T1(y)}{R(N,x)}∩
{R(A,z)}{T1(x)}{T1(z)}{R(N,y)}{R(B,z)}∪

({R(A,z)}{T1(x)}{T1(y)}{R(N,x)}∩
{R(A,z)}{T1(y)}{T1(z)}{R(N,x)}{R(B,z)}

(5)

由于{R(A,z)}{T1(x)}{T1(y)}{R(N,x)}与{R(A,z)}{T1(x)}{T1(z)}{R(N,y)}{R(B,z)}的交集中必定不含有{R(N,y)}，得到

({R(A,z)}{T1(x)}{T1(y)}{R(N,x)}∩
{R(A,z)}{T1(x)}{T1(z)}{R(B,z)})∪
{R(A,z)}{T1(y)}{R(N,x)}

(6)

由于{T1(z)}{R(B,z)}构成位移子群，得到

{R(A,z)}{T1(x)}{T1(z)}{R(B,z)}=
{R(A,z)}{T1(x)}{R(B,z)}{T1(z)}

(7)

{R(A,z)}{T1(x)}{R(B,z)}构成平面位移子群，得到

{R(A,z)}{T1(x)}{T1(y)}{T1(z)}

(8)

将式(8)代入式(6)得到

({R(A,z)}{T1(x)}{T1(y)}{R(N,x)}∩
{R(A,z)}{T1(x)}{T1(z)}{T1(y)})∪
{R(A,z)}{T1(y)}{R(N,x)}

(9)

根据式(9)得到

{R(A,z)}{T1(x)}{T1(y)}∪
{R(A,z)}{T1(x)}{R(N,x)}

(10)

从式(4)、(10)可知，能用来实现2R1T运动模式向2T1R转变的位移流形生成元应具有的形式为

{R(A,z)}{T1(x)}{T1(z)}{R(C,y)}{R(B,z)}∪
{R(A,z)}{T1(y)}{T1(z)}{R(C,x)}{R(B,z)}

(11)

根据式(11)中生成元对应的运动链为zRyPzPxRzR、zRxRzPyPzR、zRyPxRzPzR、zRxRxRzPzR、zRxRyPxRzR、zRyPxRxRzR、zRxRxRxRzR。

1.3 变自由度支链位形变换分析

以zRxRxRxRzR分支为例，如图1a支链zRxRxRxRzR中2个相邻的转轴通过一点时，可形成万向铰，可得到支链zxUxRxzU。2个zR转轴共线时，支链末端的位移流形可表示为

{R(A,z)}{T1(y)}{T1(z)}{R(C,x)}{R(A,z)}

(12)

此时支链存在一个绕z轴的局部转动自由度。当支链末端沿y轴移动有限位移，得到如图1b支链位形，此时支链末端的位移流形可表示为

{R(A,z)}{T1(y)}{T1(z)}{R(C,x)}{R(B,z)}

(13)

当支链位形如图1b所示，支链末端绕x轴做有限转动，得到图1c所示位形，此时支链末端的位移流形可表示为

{R(A,z)}{T1(y)}{T1(z)}{R(C,x)}{R(D,u)}

(14)

式(14)中1维转动流形{R(D,u)}中的 转轴u表示支链末端转轴绕x轴转动后得到的新的转动轴线。当支链处于位形图1a，支链末端位置姿态保持不变，支链存在1个绕z轴的局部转动自由度，装配在定平台上沿z轴转动后得到支链位形如图1d所示，此时支链末端的位移流形可表示为

{R(A,z)}{T1(y)}{T1(z)}{R(C,y)}{R(A,z)}

(15)

同理支链末端在进行有限位移后，得到支链位形如图1e、1f所示，从而支链末端的位移流形发生相应的变化。

图1 变自由度支链变换位形Fig.1 Transform configuration of branched chain with variable degrees of freedom

1.4 综合出的机构数目

分别从1.1节中具有2R2T位移流形的支链选取1条支链作为支链1，式(11)生成元对应的支链选取1条支链作为支链2，表1中的6自由度支链选取1条支链作为支链3，总共3条支链，连接动、静平台。第1支链，有7种支链结构；第2支链，有24种支链结构；第3支链，有7种支链结构。如果不考虑相邻两个单自由度运动副组合成多自由度运动副，也不考虑复杂运动链，则可得到7×24×7=1 176种机构构型。

2 并联机构运动模式2T1R向2R1T转变的自由度分析

2.1 2T1R运动模式自由度分析

现选取定自由度分支，即第1条支链B1A1，其结构为zRzRzRxR。选取变自由度分支，即第2条支链B2A2，其结构为zyUyRyzU。选取第3条支链B3A3，其结构为SPS。把3个支链与动平台、定平台组装后得到图2中的机构位形。

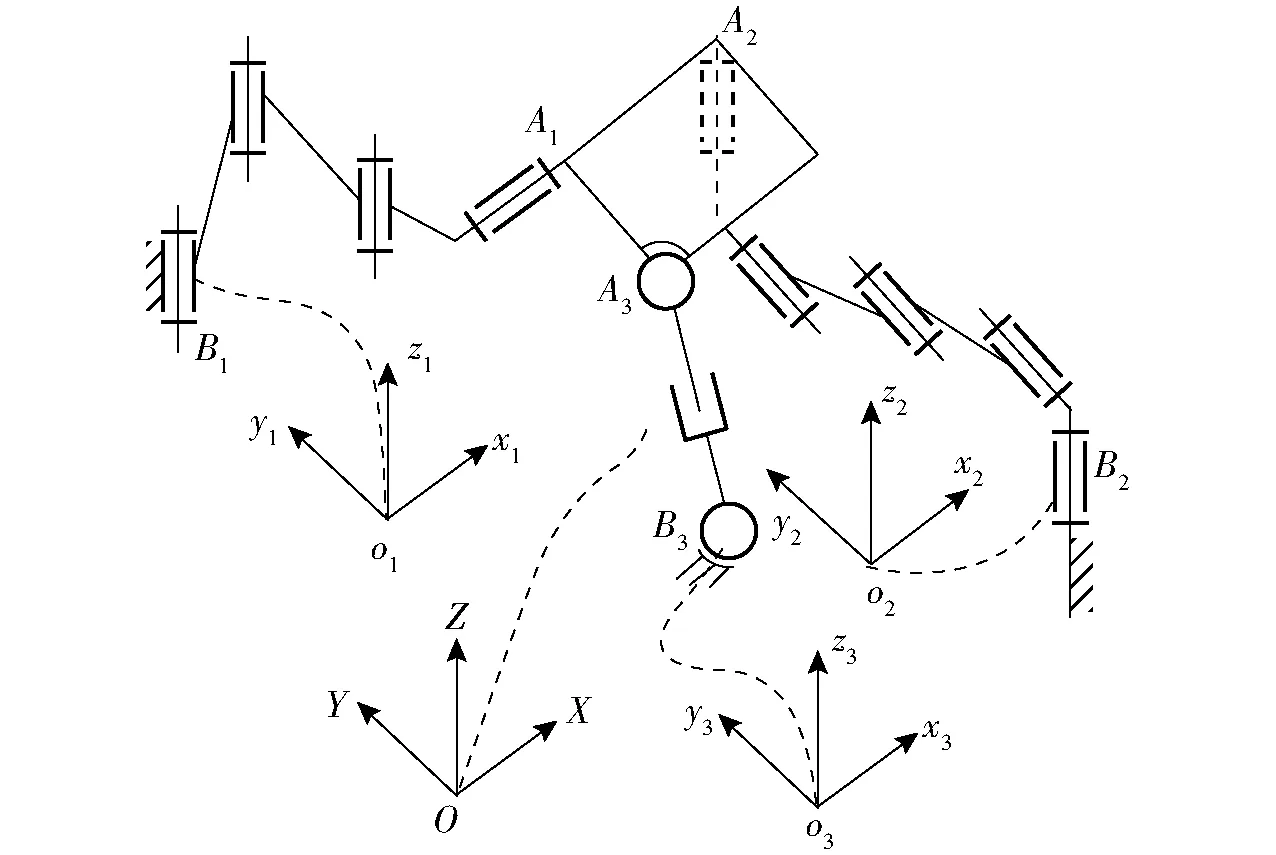
图2 具有2T1R运动模式的并联机构简图Fig.2 Schematic diagram of parallel mechanism with 2T1R motion mode

在Bi点建立坐标系Bixiyizi，图2中的第1支链在坐标系B1x1y1z1下的运动螺旋可表示为

(16)

式(16)中螺旋$ij表示支链i连接在定平台上的第j个运动副。在支链1的一般位形下，式(16)中的4个运动螺旋线性无关，支链1在坐标系B1x1y1z1下的约束反螺旋为

(17)

图2中的第2支链在坐标系B2x2y2z2下的运动螺旋可表示为

(18)

式(18)中的5个运动螺旋线性无关，支链2在坐标系B2x2y2z2下的约束反螺旋为

(19)

由于支链3不对定平台施加约束，因而动平台上施加的约束如式(17)、(19)所示，图2中动平台上所施加的1个力螺旋和2个力偶线性无关，分别限制了动平台沿定坐标Z轴的移动和沿平行于定坐标系X、Y轴的转动。动平台上施加的约束系不存在冗余约束，即υ=0。

采用修正的Kutzbach-Grübler公式计算机构自由度

M=6(n-g-1)+∑fi+υ

(20)

式中M——机构自由度

n——机构构件总数

g——机构的运动副数

fi——第i个运动副的自由度数

υ——冗余约束数

根据式(20)，可计算得到图2所示机构位形下，机构自由度为

M=6×(11-12-1)+16+0=4

(21)

由于支链3中存在绕B3A3转动1个局部转动自由度，因而图2中的动平台具有3个自由度，结合式(17)、(19)可知，动平台具有沿定坐标系X、Y轴的2个移动自由度和绕平行与定坐标Z轴的1个转动自由度,即具有2T1R运动模式。

2.2 运动模式变换过程中机构自由度分析

2.2.1支链2转轴共线位形下机构自由度分析

图2所示机构位形下，动平台沿平行于定坐标系XOY平面做有限位移后，支链2中的2个zR共轴，机构位形如图3所示。此时支链2具有1个过B2绕平行于z2轴的转轴转动的局部转动自由度。

支链3对动平台不施加约束。图3中的第2支链在坐标系B2x2y2z2下的运动螺旋可表示为

(22)

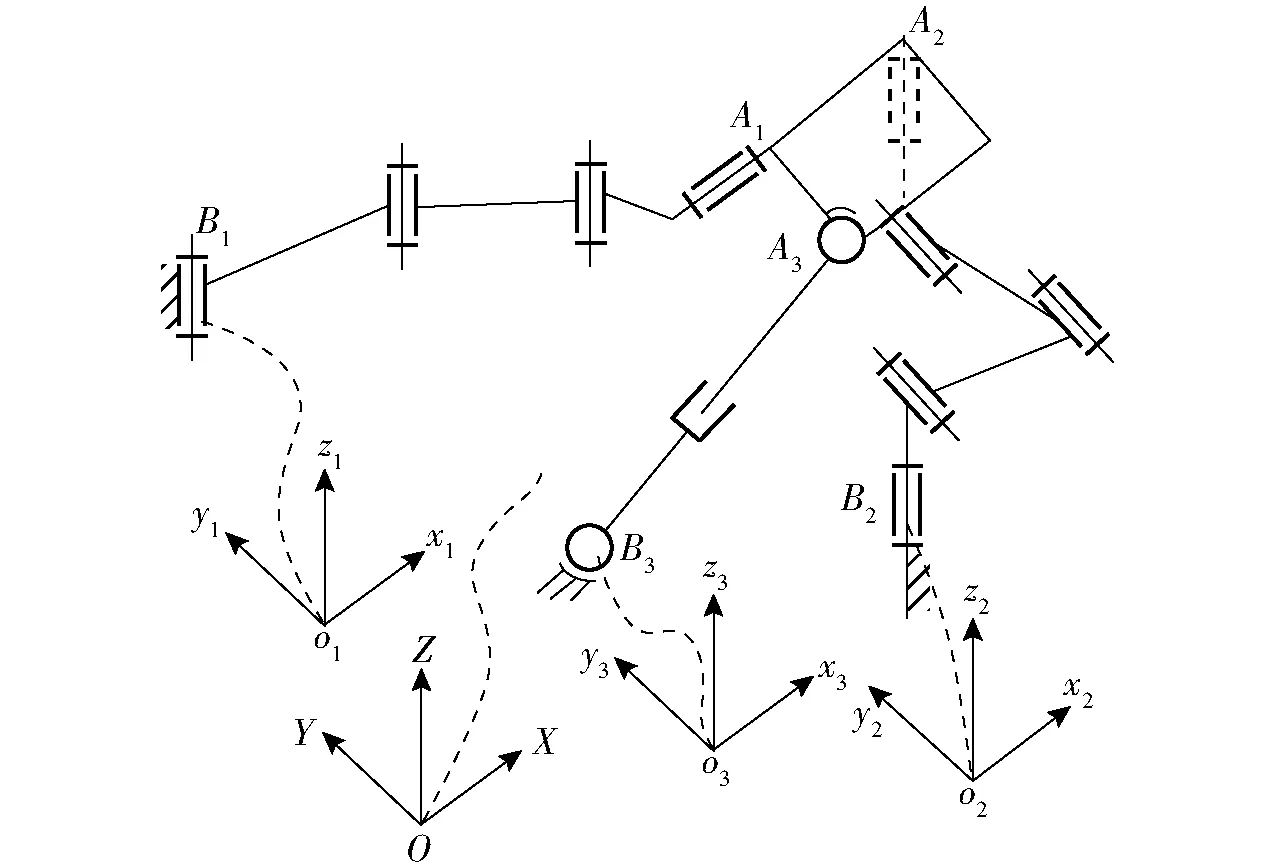
图3 支链2中两个转轴共线的机构位形Fig.3 Mechanism configuration of two rotational axes collinear in branch 2

在图3所示支链2的位形下，式(22)中的5个运动螺旋线性相关，支链2在坐标系B2x2y2z2下的约束反螺旋为

(23)

由于支链1对定平台施加的约束类型没有发生改变，并且支链3不对定平台施加约束，因而动平台上施加的约束如式(17)、(23)所示，图3中动平台上所施加的2个力螺旋和2个力偶线性无关，分别限制了动平台沿定坐标系Y、Z轴的移动和沿平行于定坐标系X、Y轴的转动。动平台上施加的约束系不存在冗余约束，即υ=0。根据式(20)，可计算得到图3所示机构位形下，机构自由度为

M=6×(11-12-1)+16+0=4

(24)

由于支链3中存在绕B3A3转动的1个局部转动自由度，支链2中存在绕B2A2转动的1个局部转动自由度。因而图3中的动平台具有2个自由度，结合式(17)、(23)可知，图3所示机构位形下，动平台具有沿定坐标系X轴的1个移动自由度和绕平行于定坐标系Z轴的1个转动自由度。当动平台沿定坐标系X轴做有限位移后，动平台又处于图2所示机构运动模式，因而图3所示机构所具有的运动模式是瞬时的。在图3所示位形下，动平台保持位姿不变，支链2过点B2绕平行于z2轴的转轴转动90°后，支链2中的平面位移子群运动链yRyRyR可变换为xRxRxR，得到图4中的机构位形。

图4 机构运动模式变换位形Fig.4 Motion pattern transform configuration of parallel mechanism

2.2.2运动模式变换位形机构自由度分析

图4中的第2支链在坐标系B2x2y2z2下的运动螺旋可表示为

(25)

式(25)中的5个运动螺旋线性相关，支链2在坐标系B2x2y2z2下的约束反螺旋为

(26)

动平台上施加的约束如式(17)、(26)所示，容易发现图4动平台所受到的2个力螺旋和2个力偶线性相关，分别限制了动平台沿定坐标系X、Z轴的移动和沿平行于定坐标系Y轴的转动。动平台上施加的约束系存在1个冗余约束，即υ=1。根据式(20)，可计算得到图4所示机构位形下，机构自由度为

M=6×(11-12-1)+16+1=5

(27)

由于支链3中存在绕B3A3转动的1个局部转动自由度，且支链2中存在绕B2A2即平行于z2轴转动的1个局部转动自由度。在图4所示机构位形下，当动平台沿定坐标系Y轴做有限移动后，支链2末端会增加一个移动自由度，此时动平台具有2R2T运动模式；当动平台绕平行于定坐标系X轴的转轴转动后，动平台具有2R1T运动模式。因而，图4所示机构位形下的运动模式具有瞬时性。

2.3 2R1T运动模式自由度分析

当动平台在图4所示位形下，沿平行于定坐标系X轴的轴线做有限转动后，机构处于图5所示位形。

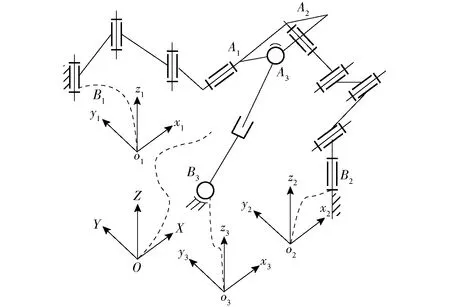
图5 2R1T运动模式的机构简图Fig.5 Schematic diagram of parallel mechanism with 2R1T motion mode

图5中的第2支链在坐标系B2x2y2z2下的运动螺旋可表示为

(28)

式(28)中的5个运动螺旋线性无关，支链2在坐标系B2x2y2z2下的约束反螺旋为

(29)

结合式(17)、(29)发现图5中动平台上所受到的2个力螺旋和1个力偶线性无关，分别限制了动平台沿X、Z轴的移动和沿平行于Y轴的转动。动平台上施加的约束系不存在冗余约束，即υ=0。可计算得到图5所示机构位形下，机构自由度为

M=6×(11-12-1)+16+0=4

(30)

由于支链3中存在绕B3A3转动的1个局部转动自由度，因而图5中的动平台具有3个自由度，结合式(17)、(29)可知，动平台具有沿定坐标系Y轴的1个移动自由度和绕平行于定坐标X、Z轴的2个转动自由度。即动平台在机构处于图5所示位形时，具有2R1T运动模式。

3 支链中驱动副的选取

一般情况下驱动副应布置在定平台上，或与定平台尽可能靠近。因而，可选取支链1和支链2中与定平台直接连接的zR转动副为驱动副，支链3中选取连接两个球副的移动副为驱动副。并联机构驱动副选取是否合理，可以通过计算锁定支链中驱动副后机构的自由度来验证。当锁定支链中驱动副后机构自由度为零，则说明驱动副选取正确。否则说明驱动副选取错误。

3.1 2T1R运动模式下驱动副合理性分析

锁定图6中虚线圆环所包含的支链1、2、3中的驱动副。

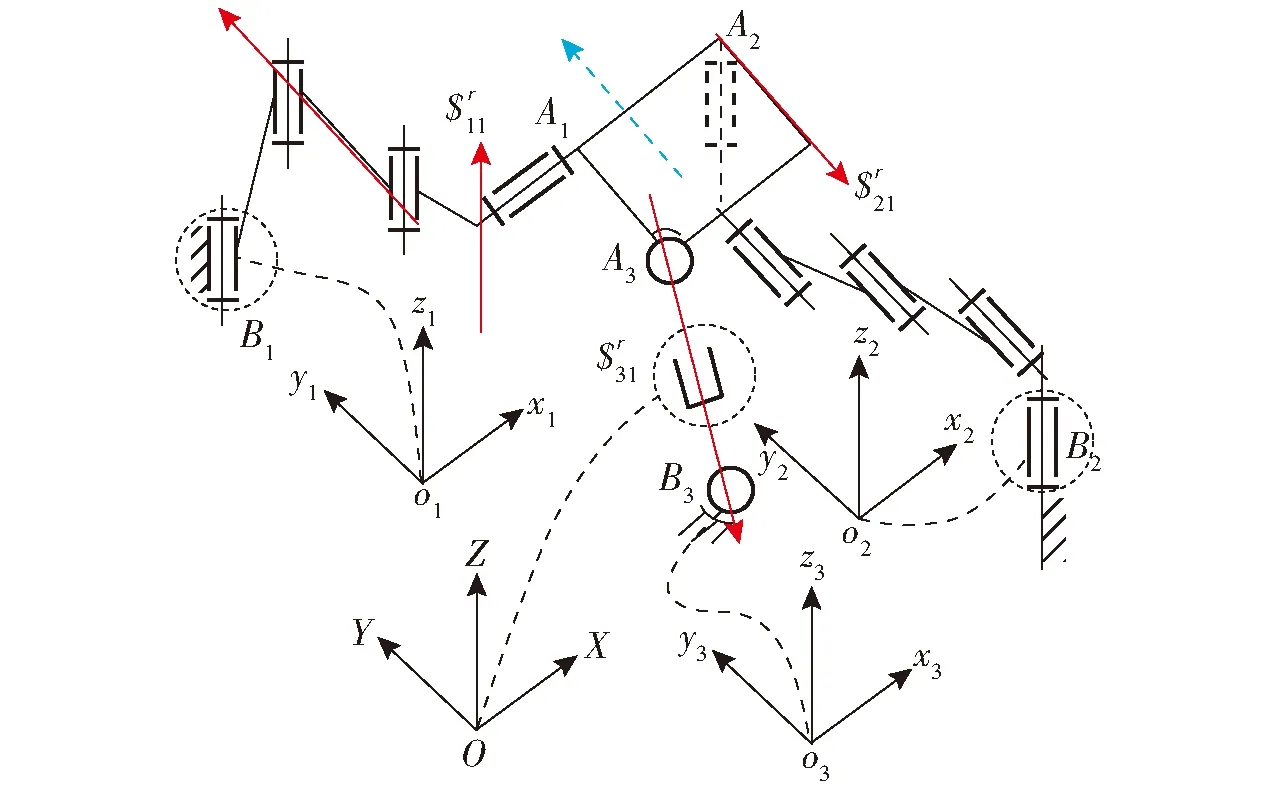
图6 2T1R运动模式下机构的驱动副布置示意图Fig.6 Schematic diagram of drive arrangement of mechanism in 2T1R motion mode

图6中的第1支链在坐标系B1x1y1z1下的运动螺旋可表示为

(31)

在支链1的一般位形下，式(31)中的3个运动螺旋线性无关，支链1在坐标系B1x1y1z1下的约束反螺旋为

(32)

式(32)中，需满足运动螺旋系与约束反螺旋互易积为零的条件，即

(33)

求解式(33)得到

(34)

图6中的第2支链在坐标系B2x2y2z2下的运动螺旋可表示为

(35)

支链2在坐标系B2x2y2z2下的约束反螺旋为

(36)

图6中的第3支链在坐标系B3x3y3z3下的约束反螺旋为

(37)

在机构的一般位形下，图6中动平台上所受到的4个力螺旋和2个力偶线性无关，分别限制了动平台沿定坐标系X、Y、Z轴的移动和沿平行于定坐标系X、Y、Z轴的转动。动平台上施加的约束系不存在冗余约束，即υ=0。根据式(20)，可计算得到图6所示机构位形下，机构自由度为

M=6×(8-9-1)+13+0=1

(38)

由于支链3中存在绕B3A3转动的1个局部转动自由度，图6中的动平台具有0个自由度。图6所示动平台在一般位形下，当支链1、2、3中驱动副锁定时，动平台不具有任何自由度，处于锁定状态。因而，在动平台具有2T1R运动模式时，驱动副的选择是合理的。

3.2 运动模式变换过程中驱动副合理性分析

3.2.1机构支链2转轴共线位形下机构驱动合理性分析

从2.2节中可知，机构运动模式变换过程中，机构处于图3位形下时，机构动平台相较图2位形下减少1个自由度，然而支链2增加一个局部自由度。很明显，在图3位形下，所选驱动副可以实现对机构的控制。

3.2.2运动模式变换位形机构驱动合理性分析

当驱动图6中的3个驱动副，使得机构处于图7所示运动模式变换位形时，锁定图7中虚线圆环所包含的支链1、2、3中的驱动副。

图7 运动模式变换位形下机构的驱动副布置示意图Fig.7 Schematic diagram of drive arrangement of mechanism in transform motion mode

图7中的第1、3支链的运动螺旋和约束螺旋形式和图6中的第1、3支链的相似，可参见式(31)、(32)、(37)。图7中的第2支链在坐标系B2x2y2z2下的运动螺旋可表示为

(39)

支链2在坐标系B2x2y2z2下的约束反螺旋为

(40)

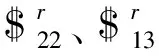
M=6×(8-9-1)+13+1=2

(41)

支链3中存在绕B3A3转动的1个局部转动自由度。支链1、2、3驱动副锁定后，机构自由度不为1，所选驱动副不能实现对动平台运动的完全控制。

3.2.3运动模式变换位形机构驱动副布置方法

并联机构在图7中运动模式变换的位形下，机构中支链2增加了一个局部转动自由度，而运动模式变换时，需要锁定支链2的驱动副。为了实现对机构的控制，可以增加一个辅助驱动副。在图8中的支链1中，在与B1处转轴相邻的转动副上布置驱动，使其在机构运动模式变换时工作。锁定图8中虚线圆环所包含的支链1、2、3中的驱动副、锁定红色圆环所包含的支链1中的辅助驱动副。

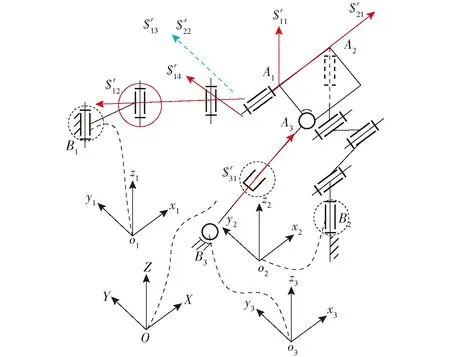
图8 支链1中增加1个驱动副的机构运动模式变换位形图Fig.8 Schematic diagram of drive arrangement of mechanism in transform motion mode with branch 1had 2 drives

图8中的第1支链在坐标系B1x1y1z1下的运动螺旋可表示为

(42)

支链1在坐标系B1x1y1z1下的约束反螺旋为

(43)

支链2在坐标系B2x2y2z2下的约束反螺旋为

(44)

图8中的第3支链在坐标系B3x3y3z3下的约束反螺旋为

(45)

在机构的一般位形下，图8中动平台上所受到的5个力螺旋和2个力偶线性相关，分别限制了动平台沿定坐标系X、Y、Z轴的移动和沿平行于定坐标系X、Y、Z轴的转动。动平台上施加的约束系存在1个冗余约束，即υ=1。根据式(20)，可计算得到图8所示机构位形下，机构自由度为

M=6(7-8-1)+12+1=1

(46)

由于支链3中存在绕B3A3转动的1个局部转动自由度，图8中的动平台具有0个自由度。图8所示动平台在一般位形下，当支链1、2、3中驱动副锁定时，动平台不具有任何自由度，处于锁定状态。因而，在支链1中增加驱动副，可以实现机构运动模式的变换。

3.3 2R1T运动模式下的驱动副合理性分析

当动平台从图8所示位形，控制支链1、2、3中的驱动副和支链1中的辅助驱动副，使得动平台做绕平行于定坐标系X轴的转轴转动后，得到如图9所示机构位形。锁定图9中虚线圆环所包含的支链1、2、3中的驱动副后，图9中机构位形下支链1、3的运动螺旋和约束反螺旋与图8所示机构位形下支链1、3的螺旋和反螺旋系形式相同。图9中的第2支链在坐标系B2x2y2z2下的运动螺旋可表示为

(47)

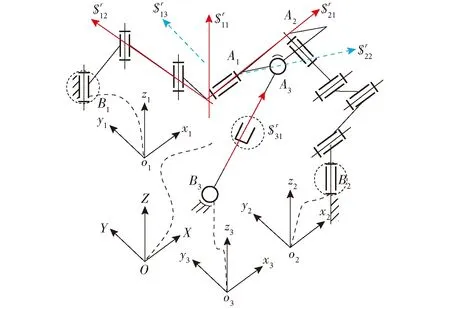
图9 2R1T运动模式下机构的驱动副布置示意图Fig.9 Schematic diagram of drive arrangement of mechanism in 2R1T motion mode

支链2在坐标系B2x2y2z2下的约束反螺旋为

(48)

在机构的一般位形下，图9中动平台上所受到的4个力螺旋和2个力偶线性无关，分别限制了动平台沿定坐标系X、Y、Z轴的移动和沿平行于定坐标系X、Y、Z轴的转动。动平台上施加的约束系不存在冗余约束，即υ=0。根据式(20)，可计算得到图9所示机构位形下，机构自由度为

M=6×(8-9-1)+13+0=1

(49)

由于支链3中存在绕B3A3转动1个局部转动自由度，图9中的动平台具有0个自由度。图9所示动平台在一般位形下，当支链1、2、3中驱动副锁定时，动平台不具有任何自由度，处于锁定状态。因而，在动平台处于2R1T运动模式时，不使用辅助驱动副可以实现对机构的控制。

综合3.1、3.2、3.3节的结果可知，提出的机构具有2T1R和2R1T两种运动模式，在支链1中增加辅助驱动副后，所选取的驱动副能实现对不同运动模式一般位形下动平台位姿的控制，因而其驱动副的选取是可行的。

4 结论

(1)通过位移流形理论和螺旋理论对2T1R运动模式向2R1T运动模式转变的并联机构进行了综合，并以一种新型的变自由度机构为例，分析了其自由度变换的位形特征，验证了其自由度的类型，确定了支链中作为驱动副的运动副。

(2)在运动模式变换时，机构的支链2增加了一个局部自由度，而运动模式变换时，需要锁定支链2。在支链1中增加了一个辅助驱动副，此驱动副只在并联机构构运动模式变换时工作，有效地实现了运动模式的变换。