基于最优初始位形的冗余度机器人可操作度优化*
唐碧秋,杨 帆,唐 焱
(桂林电子科技大学机电工程学院,广西桂林 541004)
基于最优初始位形的冗余度机器人可操作度优化*
唐碧秋,杨 帆,唐 焱
(桂林电子科技大学机电工程学院,广西桂林 541004)
冗余度机器人的初始位形对关节轨迹规划有很大影响。提出了一种基于最优初始位形的机器人可操作度优化方法,在以可操作度为性能指标对机器人的关节轨迹进行规划时,如果以优化出的可操作度最优的位形为初始位形,就可以提高执行任务初期的可操作度。算例仿真结果表明,这种基于最优初始位形的机器人可操作度优化方法可以提高机器人在执行任务开始时的可操作度,免去初期的调整过程,使其在整个运动过程中一直处于灵活性很高的位形。
初始位形;可操作度;灵活性;冗余度机器人
0 引言
冗余度机器人是指完成某一特定任务时,机器人具有多余的自由度。多余的自由度可用来改善机器人的运动学及动力学特性。灵活性的度量是冗余度机器人运动学方面的重要内容,一直是众多学者的研究对象。SALISBURY等提出了条件数[1],并用其对机器人末端的工作空间进行了评价。STEPHEN提出了兼容性指标[2],用它来衡量某一方向上力和运动的传递能力。Yoshikawa定义了机器人的可操作度这一灵活性指标,用它来度量某一位形下机器人往各个方向运动的能力[3-5]。姚建初提出了方向可操作度[6],用其作为性能指标来提高机器人基于任务方向上的运动能力。可操作度越大代表机器人灵活性越高,如何提高机器人在执行任务时的可操作度是众多学者的研究内容。文献[7]研究了能够很快使机器人离开初始奇异位形、提高机器人的可操作度的轨迹规化方法[7],就是说即使机器人的初始位形处于奇异状态或者没有达到灵活性最优的位形,也可以通过轨迹优化方法来进行调整,使机器人很快离开初始奇异位形并到达灵活性最优的位形,但这也存在一个问题,即在这个调整过程里,机器人的可操作度是很低的,即机器人的灵活性不是很高。也就是说,文献[7]没有考虑机器人的初始位形对机器人整个运动过程中的可操作度的影响。
文献[8]中提出,在对关节驱动力矩进行优化时,一个具有驱动力矩最优的初始位形对于整个运动过程中机器人关节驱动力矩的最小化优化过程是很有利的,从初始形位开始,可以在运动过程中的每一时刻将关节驱动力矩优化到最小[8]。按照上述文献[8]思路,如果在设置机器人的初始位形时就使机器人的可操作度达到最优,就可以免去机器人离开奇异位置、避开灵活性很低的位形所进行优化调整的过程,可以使机器人从初始形位开始就处于可操作度很高的位形。
因此,以可操作度为性能指标对机器人初始位形进行优化选择是非常有必要的,可以使机器人的初始位形避免处于奇异位形并使机器人的灵活性达到最优,免去初期调整的过程,使机器人在执行任务一开始就能处以可操作度最优的位形,提高机器人在执行任务初期的可操作度。
本文以可操作度为性能指标来优选机器人的初始形位,并在可操作度为最优的初始位形下以可操作度为性能指标对机器人的关节轨迹进行规划,数值仿真证明,这种基于最优初始位形的机器人可操作度优化方法可以提高机器人在执行任务开始时的可操作度,免去初期的调整过程,使其在整个运动过程中一直处于灵活性很高的位形。
1 基于最优位形的机器人可操作度优化
1.1 可操作度
设机器人某个位形下的关节从基座到机器人末端依次为关节1,关节2,…关节n。设机器人某个位形下的关节角从基座到机器人末端依次为q1,q2,…,qn。则关节向量q=[q1,q2,…,qn]T组成的空间称为关节空间。机器人末端的位置向量p=[p1,p2,…,pm]T组成的空间称为操作空间。两者变换关系为:
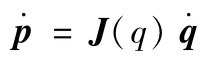
YOSHIKAWA定义了可操作度[1],如式(1)所示,并用它来评价衡量各个方向上运动能力,评价机器人整体上的灵活性。
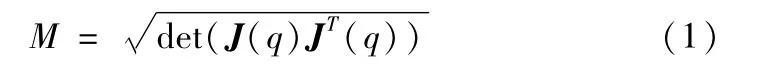
1.2 可操作度最优的初始位形
已知任务的初始末端位置及运动方向,则基于可操作度的最优初始位形选择问题可描述为数学规划模型:

在已知任务的初始末端位置时,用式(2)中的目标函数可以优选出机器人可操作度最大的初始位形。在以可操作度为性能指标,用梯度投影法对机器人的关节轨迹进行规划以提高机器人执行任务时的可操作度时,如果以优化出的最优位形为初始位形就可以避免初期的调整过程,让其在执行任务初期也保持较高的可操作度。
以可操作度为性能指标的用梯度投影法[7,9,10]具体表示为:
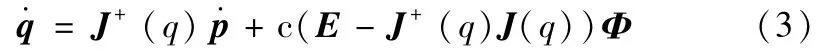
其中,c为常系数,J+(q)=JT(q)(J(q)JT(q))-1。Φ=[∂M/∂q1,∂M/∂q2,…,∂M/∂qn]T。
2 算例仿真分析
2.1 直线运动仿真
以平面三连杆冗余度机器人为例,其结构模型及关节广义坐标如图1所示。
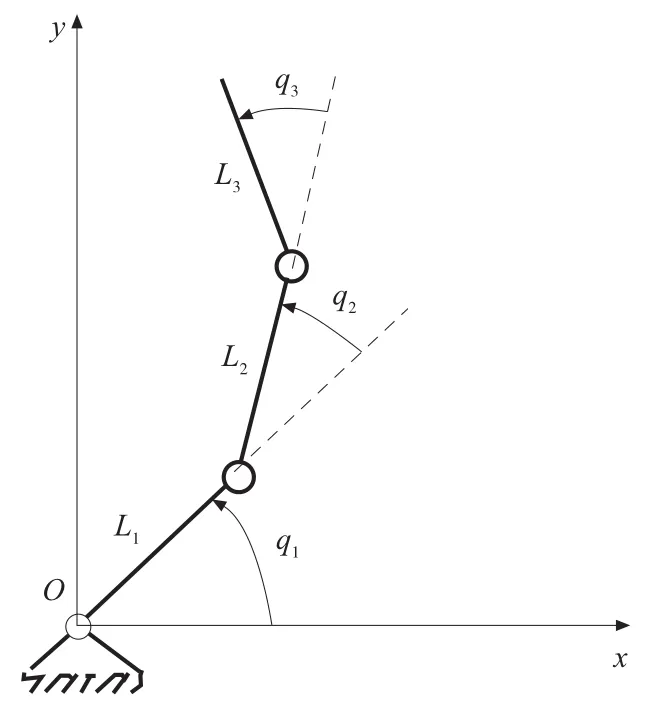
图1 结构模型
以O点为坐标原点,为方便讨论,假定关节的转动不受硬件的限制。模型数据:
杆长:L1=1m,L2=1m,L3=1m;
末端初始位置:p=[0.5,0.5]T;
末端位置可表示为(角度单位为弧度):
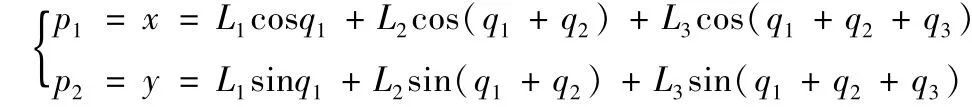
雅克比矩阵为:
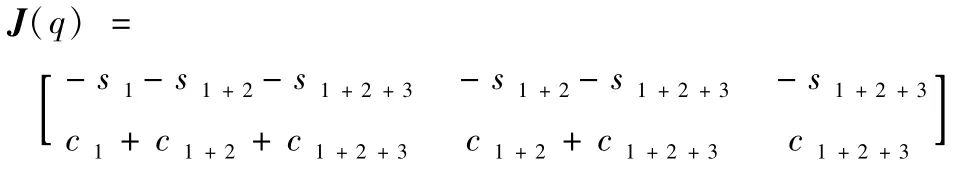
式中:
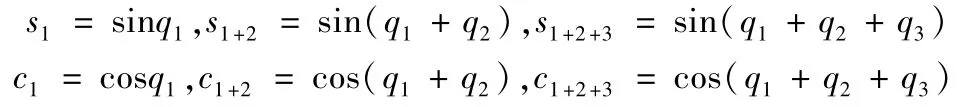
首先用式(2)中的数学规划模型对机器人的位形进行优选。数学规划模型为:
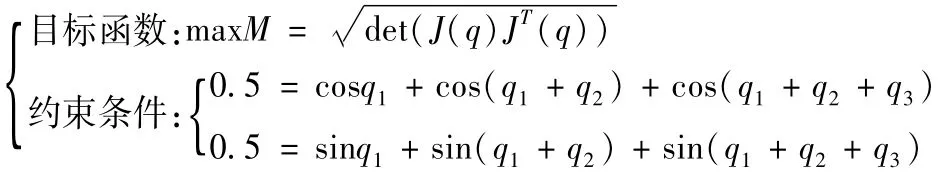
优化出的可操作度最优的位形为:
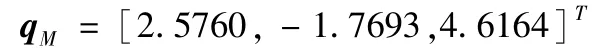
为体现最优位形的优越性,再增加两个一般位形:
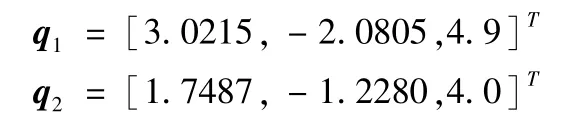
这三种位形所对应的可操作度如表1所示。最优位形的可操作度值高于另外两个一般位形的可操作度值。
分别以上述三种位形位初始位形,用式(3)中的轨迹规划方法对机器人进行关节轨迹规划。末端速度s,仿真时间为30s,c=1。
其机器人在运动过程中的可操作度的变化如图2所示。

表1 三种位形所对应的可操作度值
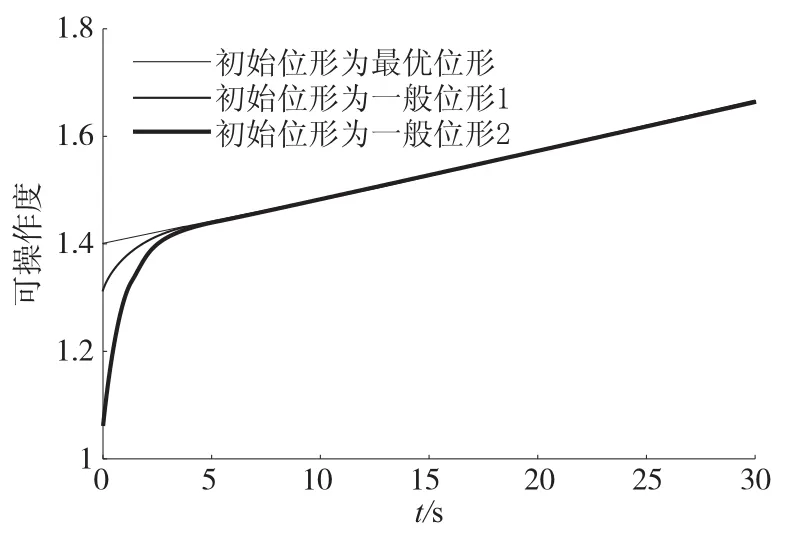
图2 可操作度变化图
从图2中可以看出,在执行直线任务时,以优化出可操作度最优的位形qM为初始位形对机器人进行关节轨迹规划,机器人在执行任务初期(执行任务的前5s)的可操作度一直是平稳变化,且高于另外两种位形所对应执行任务初期的可操作度;以一般位形q1和q2为初始位形对机器人进行关节轨迹规划时,机器人在执行任务初期(执行任务的前5s)的可操作度的变化很大,在执行任务初期的可操作度没有达到最优,而是逐步增加达到最优。以上述三种不同位形为初始位形对机器人进行关节轨迹规划时,机器人运动过程中的位形图分别如图3、图4、图5所示。图3、图4和图5中的单位为m,每两个位形之间间隔时间为5s,红色线条表示初始位形。
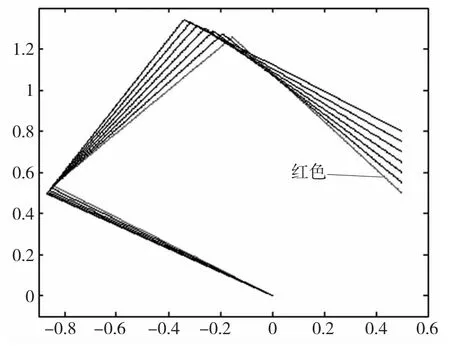
图3 初始位形为最优位形qM
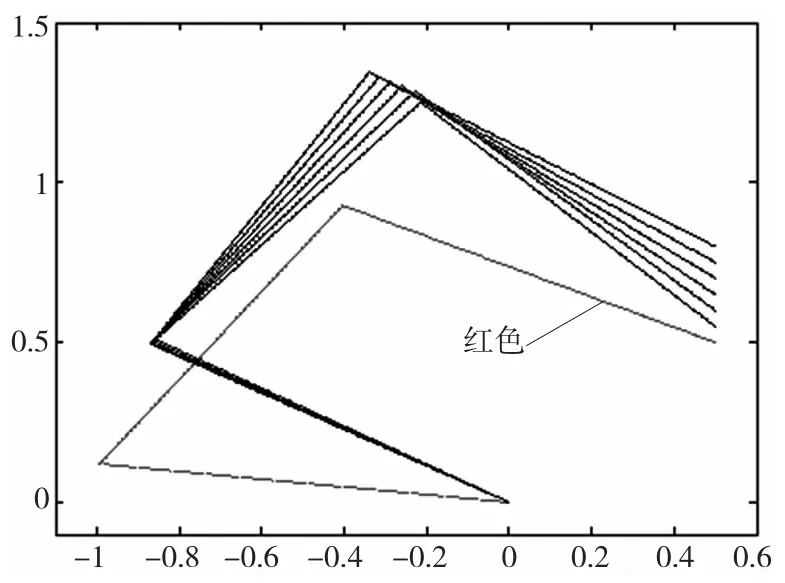
图4 初始位形为一般位形1 q1
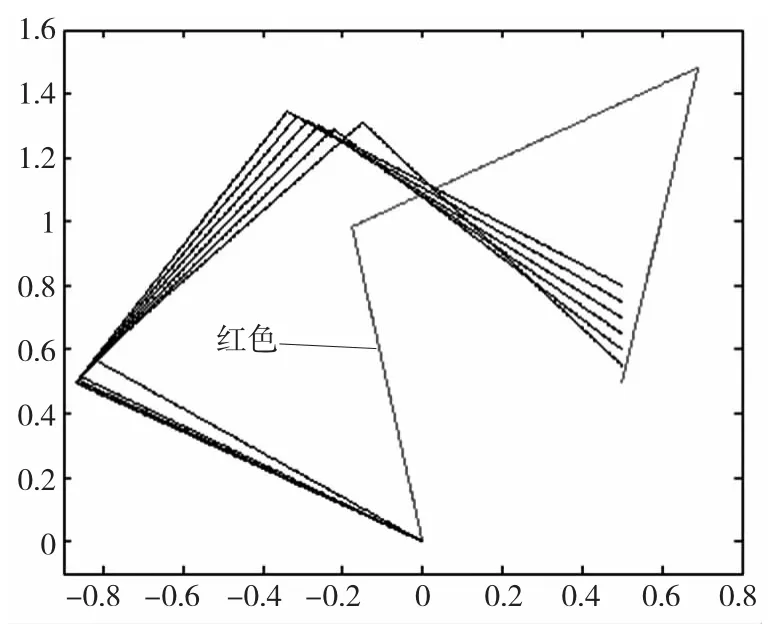
图5 初始位形为一般位形2 q2
从图4和图5中可以看出,当初始位形不是最优位形时,在初始阶段的位形变化较大,这是因为在初始阶段机器人通过很大的关节转角来调节机器人的位形,以提高机器人的可操作度,使机器人逐步调整到可操作度最优的位形。而图3中当初始位形为最优位形时,在初始阶段的位形变化比较平稳,在初始阶段不需要机器人位形的调整过程,所以没有出现很大的关节转角。
2.2 曲线运动仿真
同样以图1中的平面3R机器人为例。
初始条件为:末端初始位置:p=[0.5,0.5]T;
分别以上述直线仿真例中优化出的可操作度最优位形qM和一般位形q1、q2为初始位形,用式(3)中的轨迹规划方法对机器人进行关节轨迹规划。末端速度:p·=[0.01cos(2πt/90),0.01sin 2πt/( 90)]Tm/s,
仿真时间为90s,c=1。其机器人在运动过程中的可操作度的变化如图6所示。
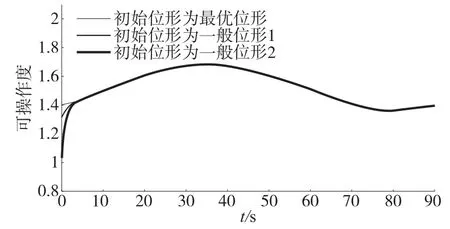
图6 可操作度变化图
同样的,从图6中可以看出,在执行曲线任务时,以优化出的位形qM为初始位形对机器人进行关节轨迹规划,机器人在执行任务初期3 结束语
(执行任务的前5s)的可操作度一直是平稳变化,且高于另外两种位形所对应执行任务初期可操作度;以一般位形q1和q2为初始位形为初始位形对机器人进行关节轨迹规划时,机器人在执行任务初期(执行任务的前5s)的可操作度的变化较大,其机器人的可操作度没有达到最优,而是逐步增加达到最优。
这种基于最优初始位形的机器人可操作度优化方法可以提高机器人在执行任务开始时的可操作度。算例仿真表明,在以可操作度为性能指标对机器人的关节轨迹进行规划时,如果以优化出的可操作度最优的位形为初始位形,就可以免去初期的调整过程,提高执行任务初期的可操作度,使其在整个运动过程中一直处于灵活性很高的位形。
[1]SALISBURY JK,CRAIG JJ.Articulated hands:Force control and kinematic issues[J].International Journal of Robotics Research,1982,1(1):4-17.
[2]STEPHEN L.Control of redundant manipulators for task compatibility[C]//Proceedings of the 1987 IEEE International Conference on Robotics and Automation,31March-3 April 1987,Raleigh,NC,Washington,DC,USA.Washington:IEEE Comput.Soc.Press,1987,4:1718-1724.
[3]YOSHIKAWA T.Manipulability of robotic mechanisms[J]. International Journal of Robotics Research,1985,4(2):3-9.
[4]MERLET JP.Jacobian,manipulability,condition number,and accuracy of parallel robots[J].Journal of Mechanical Design,2006,128:199-206.
[5]谢碧云,赵京.基于条件数约束的方向可操作度[J].机械工程学报,2010,46(23):8-15.
[6]姚建初,丁希仑,战强,等.冗余度机器人基于任务的方向可操作度研究[J].机器人,2000,22(6):501-505.
[7]梁新荣.机器人协调控制及其关节结构优化[J].五邑大学学报(自然科学版),1999(1):42-48.
[8]岳士岗,白师贤.具有最优初始位形的冗余度柔性杆机器人关节驱动力矩优化[J].北京工业大学学报,1998(1):39-44.
[9]陈安军,马学文.基于速度方向可操作度的冗余机器人关节轨迹优化[J].机械传动,2008(2):13-15,3.
[10]蒋玉杰,李景春,张国忠.关节型冗余度机器人的运动规划[J].组合机床与自动化加工技术,2005(3):50-51.
(编辑 李秀敏)
The Optimization of Manipulability for Redundant Manipulators Based on the Optimal Initial Configuration
TANG Bi-qiu,YANG Fan,TANG Yan
(College of Mechanical and Electrical Engineering,Guilin University of Electronic Technology,Guilin Guangxi541004,China)
The initial configuration has a great influence in the joint trajectory planning for redundant manipulators.A method of the manipulability optimization for redundant manipulators based on the optimal Initial configuration is proposed.It can improve the manipulability during the initial stage of the task that putting the configuration with the highest manipulability as the initial configuration in the joint trajectory planning. The result of the simulation shows that the method of the manipulability optimization for redundant manipulators based on the optimal Initial configuration can avoid the adjustment process during initial period,and it can improve the manipulability during the initial stage of the task and make manipulators be in the configuration with high dexterity.
initial configuration;manipulability;dexterity;redundancy robot
TH166;TG659
A
1001-2265(2015)01-0013-03 DOI:10.13462/j.cnki.mmtamt.2015.01.004
2014-05-15
国家自然科学基金项目(61063040)
唐碧秋(1962—),女,广西桂林人,桂林电子科技大学副教授,硕士生导师,研究领域为土木工程、机械工程,(E-mail)tbq@guet.edu. cn;通讯作者:唐焱(1962—),男,广西桂林人,桂林电子科技大学副教授,硕士生导师,研究领域为机械工程,车辆工程,精密测试技术,(E-mail)tangy51@sohu.com。

