深沟球轴承元件几何误差对回转精度的影响*
吴柏华,毛范海,董惠敏
(大连理工大学机械工程学院,辽宁大连 116024)
深沟球轴承元件几何误差对回转精度的影响*
吴柏华,毛范海,董惠敏
(大连理工大学机械工程学院,辽宁大连 116024)
根据深沟球轴承元件运动几何关系建立数学模型,空载下对轴承运动状态进行数值仿真和模拟,分析了深沟球轴承滚球直径误差、内外圈滚道圆度误差对回转精度的影响规律。结果表明,随着单一滚球误差的增加,轴承回转精度变差;多个滚球存在误差时,随着滚球的误差梯度增加,轴承回转精度变差;内外圈滚道分别存在几何形状误差时,误差阶次不变,随着误差幅值的增加,轴承回转精度变差;误差幅值不变,随着误差阶次的增加,内外圈滚道误差阶次与滚球数目具有周期性的映射关系。
深沟球轴承;元件;几何误差;回转精度
0 引言
滚动轴承作为一种应用广泛的基础件,其性能指标直接影响整个系统的精度、可靠性及寿命等。评价轴承重要指标之一是轴承回转精度。Wardle[1-2]推导出关于表面波纹度的波长和幅值与振动力的关系式。从理论分析和试验的角度来研究了推力载荷下球轴承元件表面波纹度对振动力和恒定转速下振动频率的影响。Ono[3-4]建立了球轴承两自由度的力学模型,分析了球以及外圈滚道表面波纹度对轴心的振动特性的影响规律。Okamoto[5]通过实验和数值模拟计算你的方法研究了轴承零件形状误差和轴心轨迹的关系,并给出了重复性跳动和非重复跳动的实验结果。但只是研究了外圈误差以及球的直径误差以及数量对轴心轨迹的影响规律。Noguchi[6]通过理论和实验的方式描述了轴承内外圈滚道和滚球不同误差形式和大小对轴承非重复性跳动的影响。但是模型中没有考虑接触角变化以及离心力的影响。国内方面,史文祥[7]以圆柱滚子轴承为模型,提出了对于外圈转动过程中预测旋转精度的方法,分析了外圈滚道存在误差的情况下外圈跳动量和滚道误差谐波阶次以及谐波系数之间的关系。宋飞[8]建立了基于内圈旋转分析内圈滚道误差、游隙、滚子个数对旋转精度影响的模型,得到了相关结论。赵惠玲[9]等人从滚动轴承振源入手,运用回归分析的方法得出轴承制造精度如内外套圈滚道圆度和波纹度与振动值的关系式。李传顺[10]建立了用于分析深沟球轴承非重复性跳动的五自由度静力学模型,但是模型较为复杂,且是在作用外载荷的情况下分析非重复性跳动规律。王宝坤[11]通过迭代初始给定轴心坐标,判定有效接触实现稳定状态轴心坐标的确定,从而研究圆柱滚子轴承几何误差对轴心轨迹的影响规律。目前,对于各元件误差对几何精度的影响规律及映射关系的研究尚不成熟,采用的力学模型复杂、求解方法收敛性不佳。
本文引入函数描述元件几何误差,建立空载下考虑几何误差的深沟球轴承回转精度分析的数学模型。研究滚球单一直径误差及多种误差对回转精度特性的影响规律,对从轴承零件装配组合方面提高轴承精度的研究提供理论基础。
1 轴承回转精度数学模型建立
1.1 模型假设
为简化计算,建立轴承力学模型有以下假设:
①滚球仅存在直径尺寸误差。②套圈滚道存在尺寸误差与几何形状误差。③采用刚性套圈,即滚球与滚道的接触作用不会引起套圈整体变形,滚球只作纯滚动。④不考虑弹流润滑条件以及接触角变化。基于以上假设,将轴承三维模型简化为二维模型。
1.2 轴承元件几何误差简化描述
滚球直径误差用离散的误差值表示。内外圈滚道误差采用傅里叶级数表示:

其中:θ为滚道位置角;R(θ)为θ处的半径值;D为滚道标准圆直径,k为滚道几何形状误差阶次;αk为滚道误差函数初始相位。内、外圈滚道实际轮廓半径分别表示为Ri、Re。由上式可知,滚道实际轮廓就是标准圆与多个不同周期变化的正弦曲线叠加而成。
1.3 坐标系建立
不考虑保持架、套圈挡边的影响,将滚球、内外圈滚道作为分析对象,将各元件放到所建立的坐标系中进行分析计算。坐标系系统如图1所示。

图1 坐标系系统
外圈固定,内圈转动情况下,整体坐标系(O-XY)是以外圈滚道最小二乘圆心为原点建立的,X Y平面与滚道径向平面重合,Z向沿轴承轴向。以内圈滚道最小二乘圆心为原点建立局部坐标系(Or-XrYr)。设转动坐标系与整体坐标系X方向夹角为β,即内圈转过角度为β,以逆时针方向为正。Δx,Δy为内圈圆心相对于整体坐标原点的变化量。
坐标变换的一般形式为:
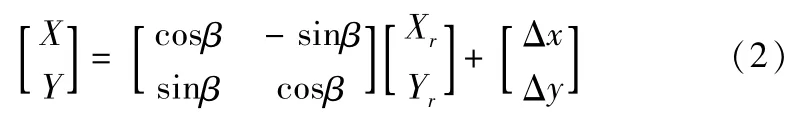
1.4 轴承元件运动几何关系
根据假设条件,内圈转动过程中,滚球相对于外圈滚道作纯滚动。内圈转过角度β,滚球公转角度为α。β与α之间的函数关系:
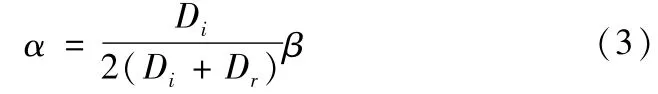
式中,Di,Dr分别为内圈滚道直径,滚球理论直径。初始状态下,滚球位置分布角度:

内圈中心无偏心位移时,坐标系O-XY中,滚球位置角为:

坐标系Or-XrYr中,滚球位置角为:

当内圈圆心相对于轴心变化量为Δx,Δy时,坐标系O-XY中,滚球位置角为:

式中Re(θ′)为外圈滚道实际轮廓函数。
坐标系Or-XrYr中,滚球中心处半径为:

上式中Dwk为滚球实际直径,

其中,Δδk为滚球直径误差,k=1~N为滚动体个数。
2 数学模型求解
通过建立的数学模型,对深沟球轴承在无载荷作用下的运动状态进行仿真分析,程序流程图如图2所示。

图2 程序流程图
(1)输入相关参数。输入轴承结构参数、滚球直径误差、内外圈滚道误差、确定转动步长后根据式(3)~(8)计算每一转动角度下滚球的位置分布角以及相应位置的内外圈滚道半径值。
(2)滚球与滚道有效接触的判定。将Lk=Rmk-Ri-0.5Dwk作为接触判定条件,若Lk>0表示滚球与内圈接触;若Lk=0,表示刚好接触;若Lk<0表示无效接触。
稳定状态即为LK中至少有两个元素为0。其他的均要大于0;以Y向正向为主方向,则发生有效接触滚球分布在Y轴两侧。
(3)最优稳态判定。在多种稳定状态中找出最佳的稳定状态,即为最优稳态判定。将有效接触滚球的中心和内圈移动坐标的原点相连,求解所有连线与Y轴的斜率绝对值之和,所求结果越小,表明滚球与Y轴的夹角越小,容易达到稳定状态。
(4)评价指标的计算。随着内圈每转过一定角度,就可求得相应的内圈中心坐标值,内圈 转过整周就可得到整个周期的中心坐标值。径向跳动指的是同一径向方向最大距离与最小值距离之差。本文精度分析指标指的是X、Y向移动量和跳动量。
3 算例及结果分析
以深沟球轴承6312为例,采用本文所建立的深沟球轴承回转精度模型,研究滚球直径误差、内圈与外圈滚道几何形状误差对轴承回转精度的影响。轴承6312的结构参数及材料属性如表1所示。

表1 轴承的结构参数
3.1 不考虑元件误差轴承回转精度各项指标计算
不考虑滚球直径误差,内外圈滚道的几何形状误差,内圈转动情况下,滚球随着内圈的转动而发生公转。Y向为内圈移动主方向。
本算例中,各个方向计算结果见表2,其中Ymax表示内圈中心Y向最大移动量,Ymin表示Y向最小移动量,Tdy表示Y向跳动值;Xmax表示X向最大移动量,Xmin表示X向最小移动量,Tdx表示X向跳动值。X向、Y向移动量变化趋势如图3所示。

表2 无误差各精度指标结果(μm)
由结果可知,Y向跳动小于X向跳动。这是由于Y向是主方向所导致的。

图3 元件无误差计算结果图
由图3可知,由于滚球公转,内圈在Y向移动量大,X向则呈现波动变化,Y向呈现周期变化。内圈在主方向跳动量小。
3.2 滚球几何形状误差与回转精度特性计算分析
为研究滚球直径误差对轴承回转精度的影响,给出不同的滚球直径误差状况,见表3。

表3 滚球直径几何尺寸误差(μm)
按照表3中误差状况进行分析,(a)是单一滚球直径误差变化对回转精度的影响;(b)误差有18组,各组之间变化梯度为0.1μm,每组各个滚动体误差变化分别为+0.1~+1.8μm。通过计算,得到图4。
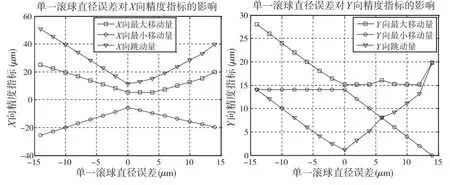
图4 Case1-a计算结果图

图5 Case1-b计算结果图
由图4可知,对于Y向指标,单一滚球直径误差为负值时,误差越小,Y向最小移动量不变,最大移动量线性减小,直径误差为正时,则变化趋势相反。对于X向指标,单一滚球直径误差为负值时,误差越小,X向最大移动量线性减小,最小移动量线性增加,直径误差为正时,则变化趋势相反。结果表明,套圈的移动量与滚球直径误差大小紧密相关,单一滚球误差越大,轴承旋转回转精度越差。
由图5可知,随着单一滚球误差梯度增加,内圈X向最小移动量和Y向最大移动量趋于稳定,X向最大移动量线性增加,Y向最小移动量线性减小。由此可知,随着滚球间误差梯度的增加,轴承的回转精度将逐渐变差。
3.3 内圈滚道几何形状误差与回转精度特性分析
为分析内圈滚道误差对回转精度的影响,给出内圈滚道误差变化状况,见表4。

表4 内圈滚道几何形状误差(μm)
按照表4进行分析,得到分析图如图6、图7所示。
由图6可知,对于三棱圆、十棱圆,误差幅值的增加会使内圈X向和Y向最大移动量增加,最小移动量减小,变化均趋近于线性。因此,误差幅值的增加使得轴承回转精度变差。
由图7可知,内圈滚道误差阶次为滚球数目一半的偶数倍时,Y向跳动量处于波峰值,X向跳动量处于波谷值;误差阶次为轴承滚球数目一半的奇数倍时,变化趋势则相反。轴承内圈移动量、内圈滚道误差阶次以及滚球数目具有周期性的映射关系。

图6 Case2-a计算结果图

图7 Case2-b计算结果图
3.4 外圈滚道几何形状误差与回转精度特性分析
为分析外圈滚道误差对回转精度的影响,给出外圈滚道误差变化状况,见表5。

表5 外圈滚道几何形状误差(μm)
按照表5进行分析,得到分析图如图8、图9所示。
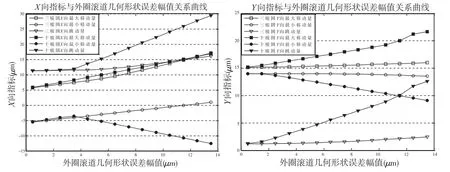
图8 Case3-a计算结果图
由图8可知,与内圈滚道对轴承回转精度影响规律一致,外圈滚道误差阶次一定时,随着误差幅值增加,轴承回转精度逐渐变差。

图9 Case3-b计算结果图
由图9可知,对于外圈滚道误差,当误差阶次低于4阶时,误差阶次对X向、Y向跳动影响较小,随着误差阶次的增加,外圈滚道误差阶次为滚球数目一半的偶数倍时,Y向跳动处于波峰值,X向跳动量处于波谷值,误差阶次为轴承滚球数目一半的奇数倍时,变化趋势则相反。这一变化规律与内圈滚道误差阶次对轴承回转精度影响规律基本一致。
4 结论
基于所建立的回转精度分析模型,编制相关的程序进行各因素的分析计算,结果表明:
(1)单一滚球误差对轴承回转精度影响很大,随着滚球误差值的增加,轴承回转精度变差。多个滚球存在误差时,随着滚球的误差梯度增加,轴承回转精度变差。
(2)内外圈滚道误差对轴承回转精度影响规律基本一致,误差阶次不变,随着误差幅值增加,轴承精度变差;误差幅值不变情况下,随着误差阶次的增加,X向、Y向跳动规律呈现周期性变化,与滚球数目成映射关系。
(3)合理的排布误差滚球和选择内外圈滚道圆度误差谐波阶数,可以减小轴承径向跳动值,提高轴承的回转精度。
[1]Wardle FP.Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearings Part1:theory. Proc Instn Mech Engrs 1988;202(C5):305-312.
[2]Wardle F P.Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearings Part2:experimental validation[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,1988,202(5):313-319.
[3]Ono K,Takahasi K.Theoretical analysis of shaft vibration supported by a ball bearing with small sinusoidal waviness[J].Magnetics,IEEE Transactions on,1996,32(3):1709-1714.
[4]Ono K,Okada Y.Analysis of ball bearing vibrations caused bY outer race waviness[J].Journal of Vibration and Acoustics,1998,120(4):901-908.
[5]Okamoto J,Ohmori T,Kitahara T.Study on Run-Out of Ball Bearings-Relation between Unroundness of Race and Locus of Shaft in Rotation[J].JOURNAL-JAPANESE SOCIETY OF TRIBOLOGISTS,2001,46(7):578-584.
[6]Noguchi S,Hiruma K,Kawa H,et al.The Influence of location of balls and ball diameter difference in rolling bearings on the nonrepetitive runout(NRRO)of retainer revolution[J].Precision Engineering,2005,29(1):11-18.
[7]史文祥.基于外圈廓形的轴承旋转精度计算及统计分析[D].河南:河南科技大学,2011.
[8]宋飞.基于内圈廓形和径向载荷的轴承旋转精度预测[D].河南:河南科技大学,2011.
[9]赵惠玲,贾峰一,李旭东,等.套圈制造精度对滚动轴承振动与噪声的影响[J].轴承,2003(12):31-33.
[10]李传顺,毛范海.深沟球轴承元件几何误差对非重复性跳动影响[J].组合机床与自动化加工技术,2013(11):9-13.
[11]王宝坤.圆柱滚子轴承元件几何误差对轴承性能的影响[D].大连:大连理工大学,2013.
(编辑 李秀敏)
Effects of Geometric Error of Deep-Groove Ball Bearing on Running Accuracy
WU Bai-hua,MAO Fan-hai,DONG Hui-min
(School of Mechanical Engineering,Dalian University of Technology,Dalian Liaoning 116024,China)
Based on the relationship between the movement and geometry of deep groove ball bearing elements,a mathematical model was established to simulate the motion state of deep groove ball bearing under unloaded.Taking the ball diameter error,inner and outer ring raceway roundness error into consideration to analysis the influence of the rotation accuracy.The results show that the rotation accuracy of bearing would be low when with the increasing of single ball errors;the rotation accuracy of bearing would be low when multiple ball exist error which with the increasing of the error gradient;the rotation accuracy of bearing would be low with the increasing of the amplitude of error when the inner and outer ring raceway geometry errors exist,but the flaps number of error was constant;there has been a periodic mapping relationship between inner/outer ring raceways flaps number of error and the number of ball when the flaps number of error was increased,but the amplitude of error was constant.
deep-groove ball bearings;element;geometrical errors;running accuracy
TH133.33;TG65
A
1001-2265(2015)01-0022-04 DOI:10.13462/j.cnki.mmtamt.2015.01.007
2014-04-17
国家自然科学基金(51375065)
吴柏华(1988—),男,武汉人,大连理工大学硕士研究生,研究方向为滚动轴承及轴系精度特性与刚度特性研究,(E-mail)berwalled@ sina.com。

