基于非均匀毛细管结构的纱线导水机理
范 杰,齐园园,李彩霞,刘 雍
(天津工业大学纺织学院,天津 300387)
纱线的液态水传输对服装的热湿舒适性具有重要的影响,尤其对于提高运动服装的舒适性及防护服装的作业效率至关重要[1-3].织物中大多存在不同尺度的孔隙,包括纱线内纤维间的小孔和纱线间的大孔,其中纱线内纤维间的小孔对于织物的导水性能具有重要意义[4-5].纱线内纤维间的水分传导由毛细管压力驱动,其水分传递性能取决于液体的性质、液体和纤维表面的相互作用及纱线中毛细孔隙的形态[6-8].液体的表面张力、粘度及固液接触角可以通过实验测定,而纱线内部的孔隙结构是复杂并难于准确表达的.
以往对纱线导水机理的研究,多采用Lucas—Washburn方程,在假设纱线内部孔隙为均匀光滑毛细管的基础上进行研究[9-10].在实际生产与应用中,由于纱线加捻,纤维在纱线截面上内外转移,纱线内部的毛细管大多是不均匀的,即纱线内的毛细管沿纱线长度方向没有固定的横截面形状,而非均匀毛细管对于毛细芯吸行为具有重要的影响[11].Erickson等[12]发现非均匀毛细管的浸润能力明显低于均匀毛细管,且均匀毛细管直径的任何变化都必然会减慢总的润湿速度.Young[13]通过构造一个简单的公式来模拟非均匀毛细管的芯吸流动,得到了同样的结果.Shou等[14]建立具有半径递减的非均匀毛细管流动时间方程,研究发现半径递减的两节毛细管较具有相同高度和体积的均匀毛细管具有更快的芯吸速率.上述对非均匀毛细管芯吸行为的研究表明,毛细管的形态结构对芯吸流动具有重要的影响.
对纱线导水性能的实验研究表明,纱线的芯吸性能与纱线中纤维的直径和纱线捻度密切相关[15-17].对某一纱线而言,加捻导致纤维在纱线中排列形式变化而引起的纱线中毛细管非均匀结构加剧对纱线的芯吸性能产生重要影响[15].由此可见,纱线中非均匀毛细管的结构变化是影响纱线的芯吸导水性能的重要因素.
尽管纱线中的毛细芯吸导水现象已被广泛研究,但基于非均匀毛细管结构进行的纱线导水机理研究尚未见报道.本研究通过建立N节藕节非均匀毛细管模型研究纱线内部非均匀毛细管的毛细芯吸流动行为.并采用不同单丝线密度和捻度的尼龙长丝纱进行芯吸实验,对N节藕节非均匀毛细管模型进行实验验证,为运动和防护服装的纱线设计和优化提供理论依据.
1 藕节非均匀毛细管模型的建立
当纱线中的毛细管发生芯吸流动时,液体会在毛细压力作用下自发地沿着连续的毛细管通道发生流动.对于纱线的芯吸过程,连续的毛细管会在纤维发生转移时产生变形,导致连续毛细管的非均匀化结构[18-19].为了研究纱线内部非均匀毛细管的芯吸流动,本文建立了非均匀毛细管的N节藕节非均匀毛细管模型[5],如图1所示.N节藕节非均匀毛细管由交替的粗节和细节构成,细节和粗节的高度比n和宽度比m及交替频率取决于纱线中纤维的线密度和纱线的捻度.
进一步对图1中的N节藕节非均匀毛细管模型进行如下说明:
(1)忽略重力.
(2)芯吸以藕节非均匀毛细管的粗节为起点.
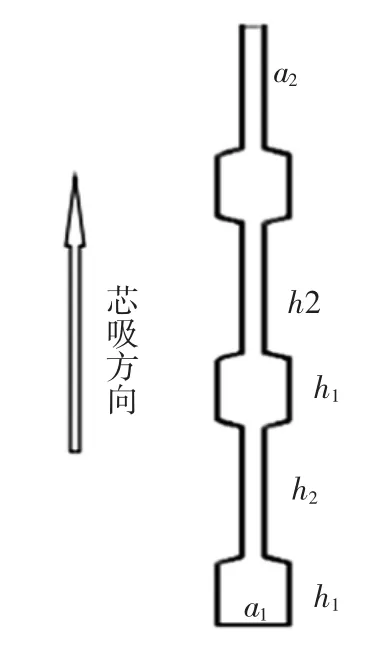
图1 N节藕节非均匀毛细管模型Fig.1 Model of N-section lotus-rhizome-node-like non-uniform capillary model
(3)藕节非均匀毛细管的粗节和细节总数为偶数.
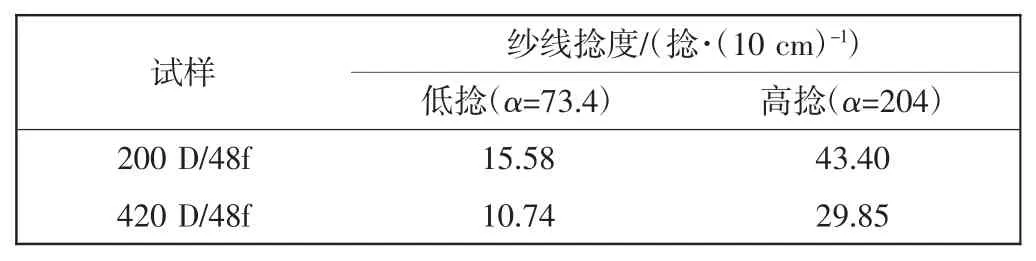
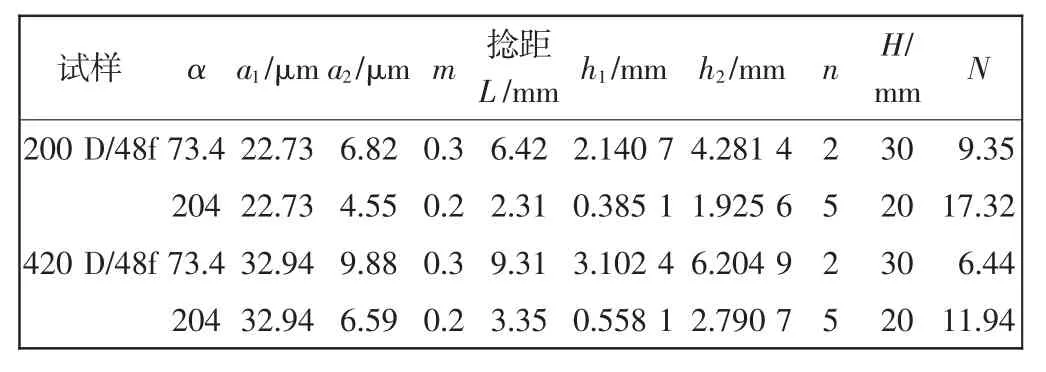
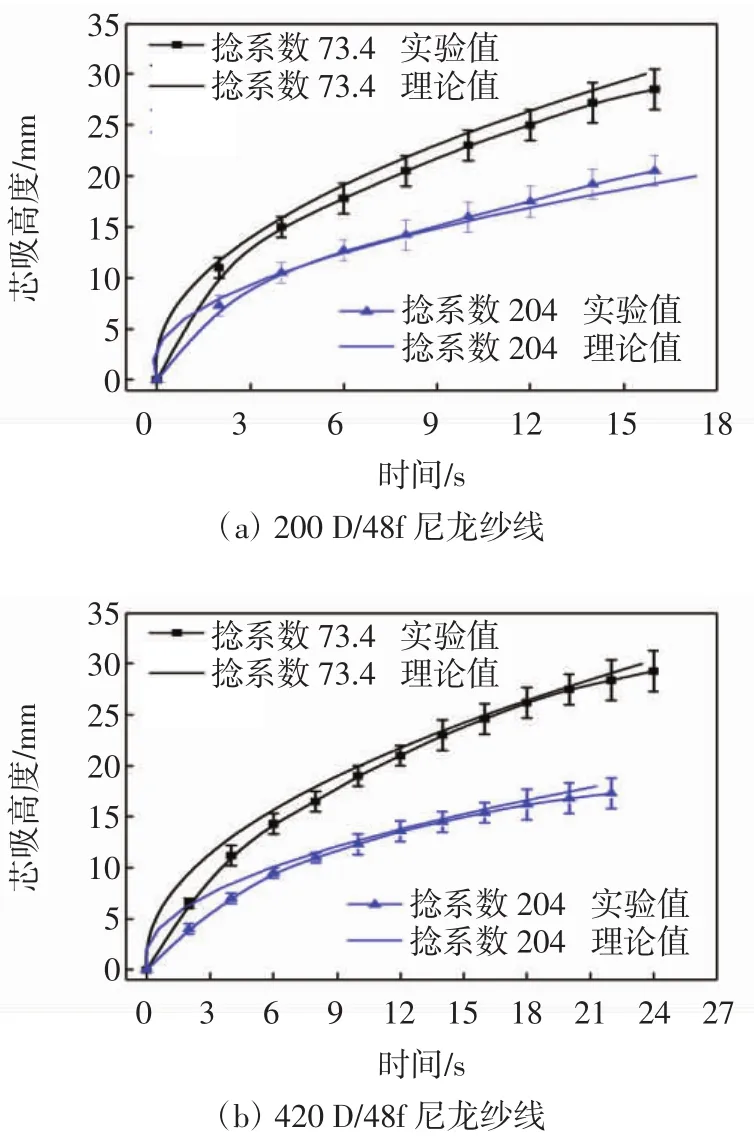
(4)粗节的宽度和高度别为a1和h1,细节的宽度和高度别为a2和h2,粗节的长度小于细节,即h1 定义: 式中:n为藕节非均匀毛细管的细节与粗节高度之比,n>1;m为细节与粗节宽度之比,1>m>0. 根据达西定律和平板泊肃叶定律: 式中:Q为流量;u为平均流速;Κ为液体的渗透张量;η为流体的动态粘度;Δp为沿液体流动方向单位距离的压强差.得到粘性流动时液体流过第1节管时流体的静压力降为: 此时毛细管的毛细压力为: 根据芯吸平衡时静压力降和毛细压力相等,可得: 通过对式(5)积分,可以得到液体充满第1节管所需的时间为: 当液体流至第2节管时, 且 此时, 由于芯吸平衡时静压力降和毛细压力相等,通过积分可得液体充满第2节所需的时间为: 根据以上原理,类推得到液体充满N节藕节非均匀毛细管第N节所需时间为: 式中:N为偶数. 由此计算得到液体充满N节藕节非均匀毛细管的芯吸时间方程为: 式(13)表明:非均匀毛细管的芯吸时间与构成非均匀毛细管的总管节数、粗细节长度比、粗细节宽度比和粗细节的几何尺寸有关. 本实验选用浙江嘉华特种尼龙有限公司生产的200D/48f(单根长丝线密度为4.17D,1D=9tex)、420 D/48f(单根长丝线密度为8.75 D)2种不同单丝线密度的无捻尼龙纱线作为原材料,采用DSTW-01型数字并捻机,以2种捻系数(α)对无捻尼龙长丝纱进行加捻,再在高温高压下对加捻纱定捻2 h,得到表1所示4种不同结构参数的尼龙纱线. 表1 尼龙纱线结构参数Tab.1 Structural parameter of Nylon yarn 实验所用仪器包括:DSTW-01型数字并捻机,天津市嘉诚机电设备有限公司产品;TM3030型扫描电子显微镜,日本日立公司产品;芯吸实验装置,自制;JC2000C型接触角测试仪,上海中晨数字技术设备有限公司产品;JYW-200A型表面张力仪,承德鼎盛试验机检测设备有限公司产品;SNB-1型数字粘度计,上海方瑞仪器有限公司产品. 鉴于芯吸过程重力可以忽略,因此,采用垂直芯吸实验对不同结构参数纱线的芯吸现象进行观察,实验装置如图2所示. 图2 芯吸实验装置示意图Fig.2 Schematic drawing of wicking experimental apparatus 实验时,将纱线的顶端固定于支架的固定端,纱线低端施加0.01 N张力,刻度尺与垂直纱线平行放置用于测量不同时间的芯吸高度.将装有0.5%亚甲基蓝水溶液的水槽放置在升降台上.实验开始后水槽随升降台快速上升将纱线低端淹没,用摄像机记录不同时间的芯吸高度,直到达到芯吸平衡. 采用TM3030型扫描电子显微镜对所得加捻长丝纱线的表面形貌进行观察;采用接触角测试仪测量尼龙单纤维与0.5%亚甲基蓝溶液的接触角;采用表面张力仪测量亚甲基蓝溶液的表面张力;采用数字粘度计测量亚甲基蓝溶液的粘度.测试温度均为20℃. 图3为不同单丝线密度和不同加捻程度的加捻尼龙长丝纱扫描电镜图. 图3 尼龙长丝纱的扫描电镜图Fig.3 Scanning electron microscopy images of Nylon filament yarn 图3表明:低捻长丝纱具有较大的捻距,而高捻长丝纱具有较小的捻距;高捻长丝纱中长丝的内外转移频率高于低捻长丝纱.具有相同捻系数的纱线几乎具有相同的外观特征. 依据图3中的SEM图像,测得低捻纱线的细节和粗节长度比为2,而高捻纱线细节和粗节长度比为5,相同捻系数的纱线具有相同的细节/粗节长度比n. 由图3可知,纱线中长丝约在每个捻回发生一次内外转移,由纱线的捻度和捻系数的关系式(式(14))、纱线的捻距计算公式(式(15)),及式(16)计算得到各纱线粗细节高度h1、h2、一个捻回的捻距L及某芯吸长度的粗细节总数N: 式中:T为捻度;α为捻系数;D为纱线旦数;L为捻距;h1、h2分别为粗、细节高度. 图4为长丝堆积结构示意图. 图4 长丝堆积结构示意简图Fig.4 Schematic drawing of filament stacking structure 假设长丝纱中的长丝在加捻产生的垂直于纱轴的法相压应力作用下紧密排列,当长丝在纱线截面上不发生转移时,长丝相互平行呈四边形(图4(a))或三角形(图4(b))密堆式排列[17],形成非均匀毛细管的细节区域,其直径a2为3根(高捻)或4根(低捻)平行紧密排列长丝所构成的孔隙的当量直径.当长丝在纱线截面上发生转移时,长丝将由纱线的内层向外层转移或由外层向内层转移,此时,构成非均匀毛细管细节区域的纤维密集平行排列形式被打破,变化为由6根长丝密集排列的松散堆砌方式,形成非均匀毛细管的粗节区域,如图4(c)所示,其直径a1为6根平行紧密排列长丝所构成的孔隙的当量直径. 纱线内单根长丝直径可由式(17)计算得到: 式中:d为单根长丝直径(μm);D为纱线旦数;nf为纱线内长丝根数;γ为纤维密度(g/cm3). 通过简单的几何计算,可以得出粗节直径a1=1.143 7 d,低捻时细节直径a2=0.390 2 d,高捻时细节直径a2=0.225 7 d.因此可以得到,低捻时粗细节宽度比m≈0.3;高捻时粗细节宽度比m≈0.2. 由以上分析计算可得4种尼龙长丝纱的结构参数,如表2所示,毛细管长度为60 mm. 表2 尼龙长丝纱中非均匀毛细管的结构参数Tab.2 Structural parameter of non-uniform capillary channel of Nylon filament yarns 实验测得20℃时,0.5%亚甲基蓝水溶液的表面张力为 65.5×10-3N/m,粘度为 1×10-3Pa·s,0.5%亚甲基蓝水溶液在尼龙单丝表面的接触角为50°.由式(6)计算得到: 将表2中计算得到的各尼龙长丝纱结构参数和参数C值带入式(13)中得到各纱线的理论芯吸高度-时间曲线,并与其实验芯吸高度-时间曲线做比较,结果如图5所示. 图5 不同结构尼龙长丝纱的理论和实验芯吸高度-时间曲线Fig.5 Theoretical and experimental wicking height-time curves of Nylon filament yarn with different structural parameters 由图5可以看出,对于同种纱线而言,加捻程度高的纱线(捻系数204的纱线)较加捻程度低的纱线(捻系数73.4的纱线)具有更快的芯吸速率和更高的芯吸平衡高度.纱线的捻度对于纱线的芯吸速率和芯吸平衡高度具有显著影响.这是由于在一定芯吸高度内,捻系数高的纱线具有更大的粗细节总数N(见表2),更大的管节数表明非均匀毛细管的粗细节交替频率更高,从而导致非均匀毛细通道的不均匀性增加,因此,纱线的芯吸速率随纱线加捻程度增大而降低. 对比图5(a)和图5(b)中不同单丝线密度的尼龙纱线芯吸-高度时间曲线,可以看出,单丝线密度大的长丝纱(420 D/48f)较单丝线密度小的长丝纱(200 D/48f)具有更快的芯吸速率.由纱线的电镜图片(图3)可以看出,具有相同捻系数的纱线具有相似的外观,由此可推断具有相同捻系数的纱线中,非均匀毛细芯吸管道具有相似的结构特征.因此,不同单丝线密度的长丝构成的具有相同捻系数的纱线中,非均匀毛细管具有自相似的结构特征.由于单丝线密度大的纤维之间形成的非均匀毛细芯吸管更大,因此具有更高的芯吸速率. 本文根据达西定律和毛细压力方程建立了非均匀N节二维藕节毛细管模型,研究长丝纱中非均匀毛细管的芯吸流动,得到N节二维非均匀毛细管的芯吸高度-时间方程;对不同单丝线密度的无捻尼龙长丝以不同捻系数加捻,以构造具有不同几何结构的非均匀毛细管,对其芯吸性能进行实验研究.理论和实验研究结果表明,液体的芯吸流动速率和芯吸平衡高度极大地依赖于非均匀毛细管的结构形态.加捻程度高的纱线因粗细节频繁交替导致毛细管非均匀程度提高,从而具有较低的芯吸速率和芯吸平衡高度;单丝细度高的长丝纱具有较粗的非均匀毛细管,从而具有较高的芯吸流速.2 藕节非均匀毛细管的芯吸时间方程

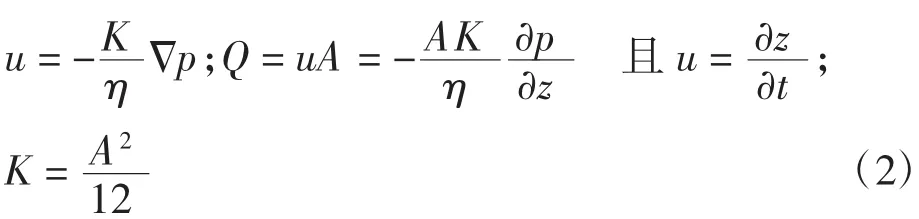
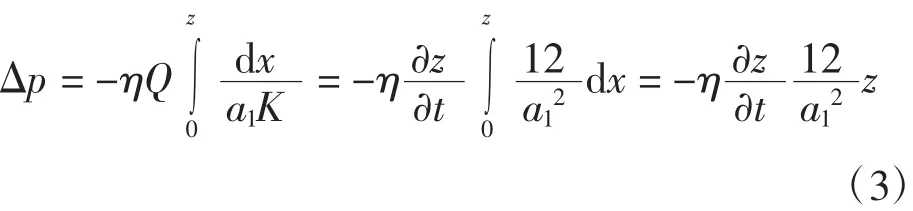




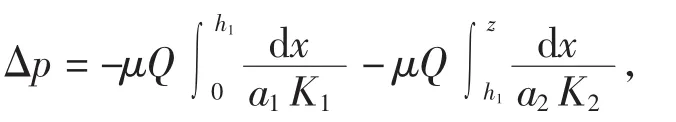
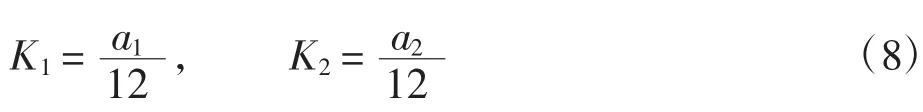

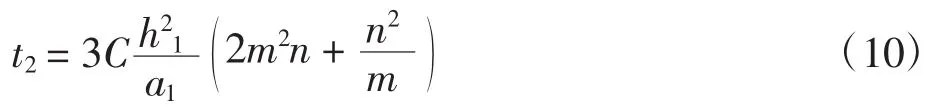

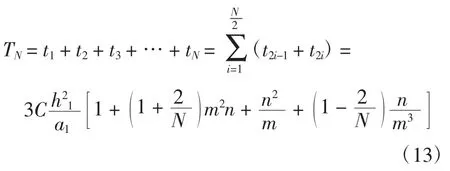
3 实验部分
3.1 实验材料和仪器
3.2 纱线芯吸实验
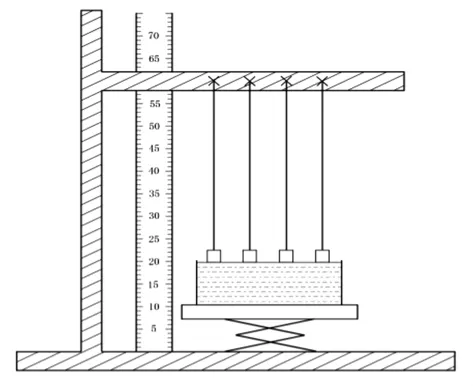
3.3 结构表征和性能指标测试
4 结果与讨论
4.1 纱线形貌

4.2 纱线的结构参数计算


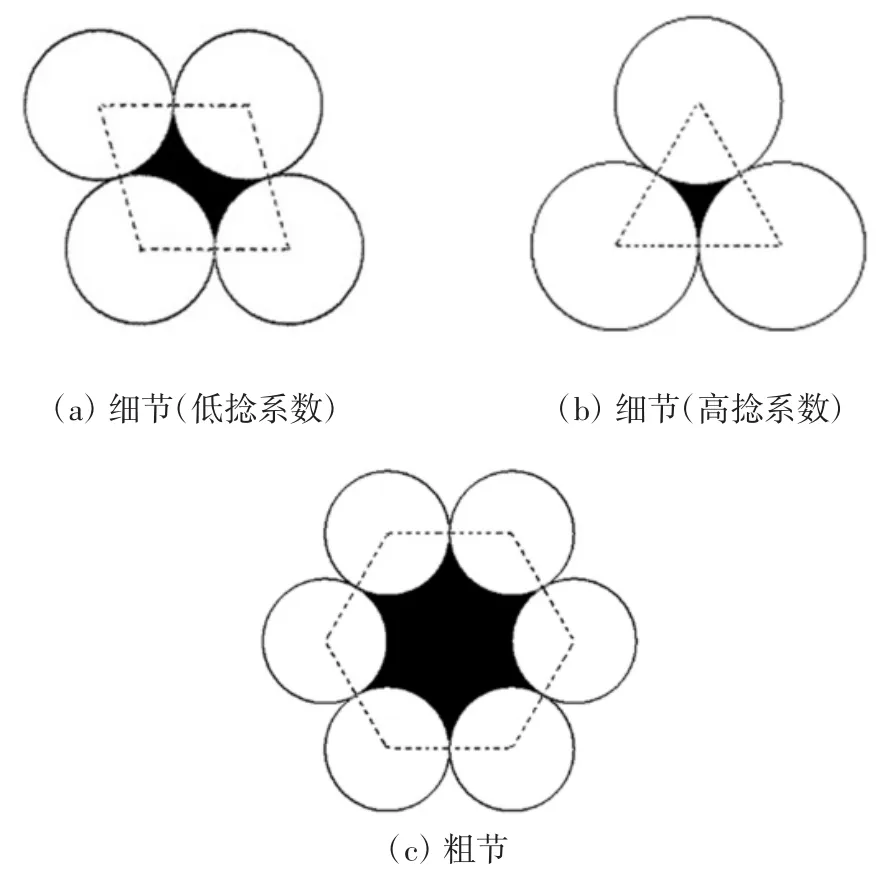

4.3 非均匀毛细管模型的实验验证
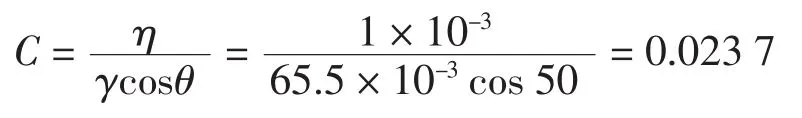
5 结论

