基于改进Logistic回归与不变矩的螺钉滑牙检测方法

郭庆华 ，王家豪 ，宋丽梅 ，杨怀栋

（1.天津工业大学 电气工程及自动化学院，天津 300387；2.清华大学 精密仪器系，北京 100084；3.伍伦贡大学 计算机、电气工程与通信工程学院，伍伦贡 2500，澳大利亚）

目前，在生产制造业方面，工业机器人自动系统已发展得比较成熟，比如瑞士的ABB工业机器人系统，日本的Nachi工业机器人系统，都有一整套的解决方案.然而在产品检测部分，尤其是高精度检测部分，尚属于国内外学术界研究的热点[1-4].检测作为工业生产制造过程必不可少的环节，正制约着生产自动化的发展.市场上主流的自动工业检测设备大多采用激光或者光谱共聚焦设备，虽然精度很高，有些甚至能达到纳米级的精度，但是造价高昂，而且其采集到的数据量庞大且冗余信息过多，从中提取感兴趣区域ROI（region of interest）会耗费大量的时间，这直接影响了算法的优化.所以基于计算机视觉的工业检测方向一直是国内外研究的前沿与热点.在过去几年中，大多数研究都集中在产品外观、包装以及大中型工业部件表面曲率是否合格、产品凹坑、加工精度是否符合要求等方面，对于螺钉、铆钉这类涉及精度较高的微小零部件的检测还很少有人研究[5].

2010年Kosarevsky等[6]提出了利用3D扫描仪对螺钉滑丝情况的检测，并给出了评价方法.2013年Latypov等[7]在Sergey Kosarevsky基础上进行了点云重建并提出了新的评价方法.2016年，Cha等[8]基于霍夫变换和支持向量机实现了对螺钉松脱方面的检测与测量.由此可以看出，使用机器视觉的检测系统的被测对象正向着小型化、高精度的方向发展.然而传统的基于机器视觉的检测方法准确度低，且传统的支持向量机算法需要多轮迭代才能收敛，需要较长的学习时间[9].基于此，本文提出利用计算机视觉结合改进logistic回归分类器对螺钉滑牙进行检测的方法，并搭建出基于此方法的测量系统，以解决传统机器视觉方法精度低、采用机器学习算法训练时间过长等问题.

1 检测平台的搭建

本研究采用型号为PointGrayGS3-U3-51S5M的工业CCD相机，镜头为Schneider 11 mm焦距镜头，当被测物体表面与相机距离为28.3 cm时取得最佳成像，经实验测得，每像素代表的实际大小为0.010 4 mm.本系统选用条形光源进行补光.实验平台如图1所示.

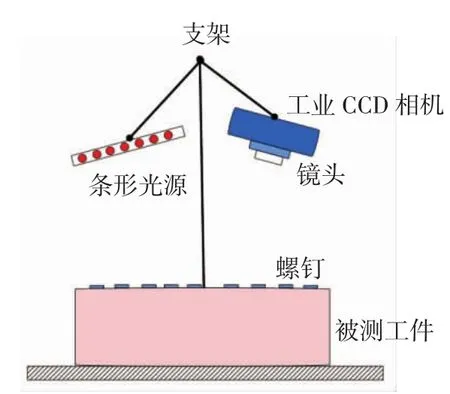
图1 实验平台示意图Fig.1 Sketch map of experiment platform

2 系统工作流程与关键算法

2.1 系统工作流程

系统工作流程如图2所示.

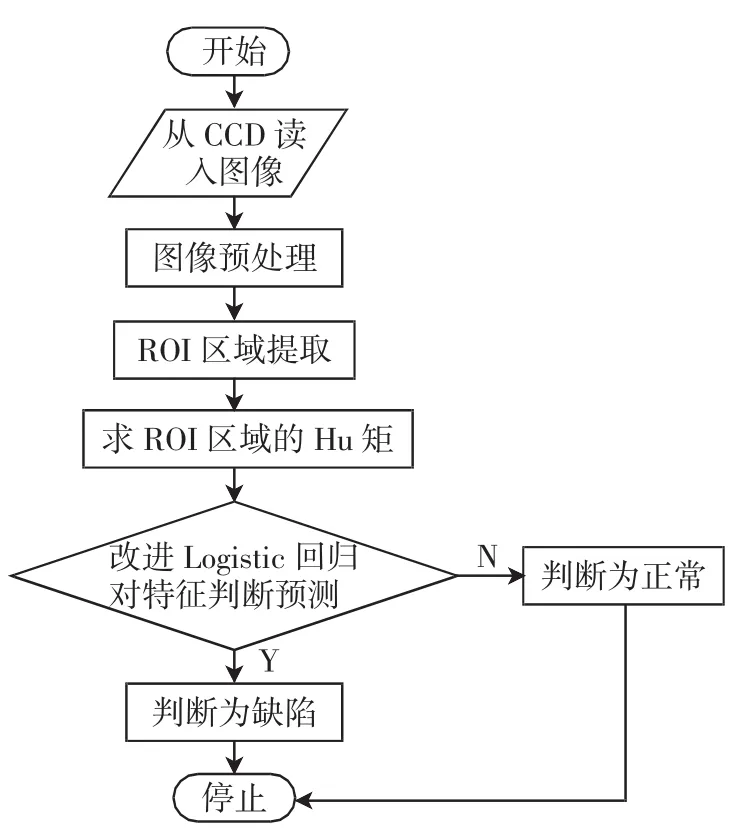
图2 工作流程图Fig.2 System flow chart

（1）图像预处理部分：主要对CCD采集的图像进行滤波，在去除噪声的同时增强图像边缘，提高ROI提取的精度.

（2）ROI提取部分：首先对预处理后的图像进行阈值二值化，然后进行霍夫圆变换，提取螺钉的位置.

（3）特征提取部分：计算每个ROI处的Hu矩.

（4）判断预测部分：用训练好的Logistic回归分类器对输入的7个Hu矩进行判断.

2.2 关键算法

2.2.1 ROI提取算法

在ROI提取方面，主要采用了霍夫变换的方法，将图像中特定大小的圆（即螺钉）的圆心位置、半径求出，即确定了ROI区域.

霍夫变换是一种基于投票累加器的算法[10]，对于霍夫圆变换的参数方程为：

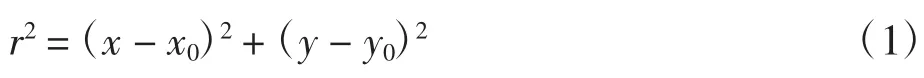
由式（1）可见，由于方程含有3个未知量，如果构建累加器则需要3个维度.为了节约时间及算法对内存的占用，将霍夫圆变换分为2个步骤[11]：首先引入一个检测圆心（ai，bi）的累加器.使用一个边缘探测器检测圆心周围明显的边缘点.由于圆周上的边缘点的梯度应该指向半径方向，所以，在找到可能的圆心的情况下，建立一维的半径直方图，则直方图峰值对应的是检测到的圆的半径.

2.2.2 特征提取算法

不变矩是由Hu提出的，其利用中心矩构造出7个不变量，能够对区域形状进行描述，而且具有平移、比例、旋转不变性，在计算机视觉中是一种十分重要的特征描述方法[12].

对于分布为f（x，y）的灰度图像，定义其（p+q）阶矩为[13]：

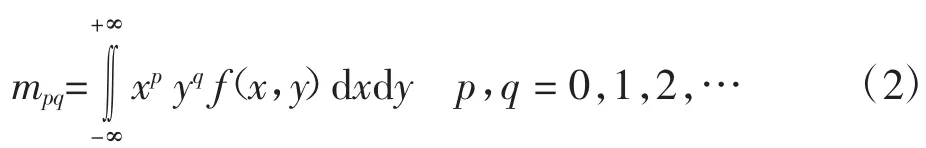
且对应的中心矩定义为：

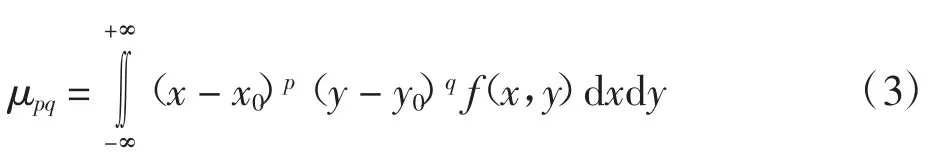
由于数字图像的分布是不连续的，所以将矩函数与中心矩函数离散化：

定义归一化中心矩为：

Hu利用二阶、三阶中心矩构造出了7个不变矩，其在连续图像条件下可保持图像平移、缩放、旋转不变性[14].具体定义如下：

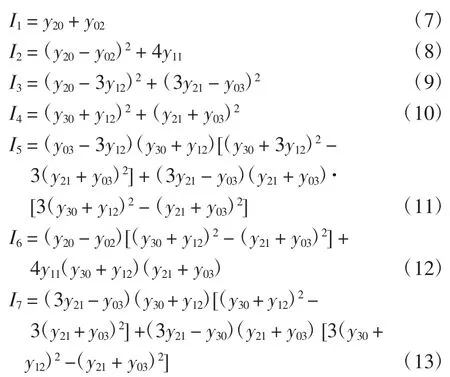
2.2.3 分类判别算法

Logistic回归是业界最常用的分类器之一，其对线性可分的数据有良好的分类效果与分类精度[15-16].Logistic回归工作原理如图3所示.

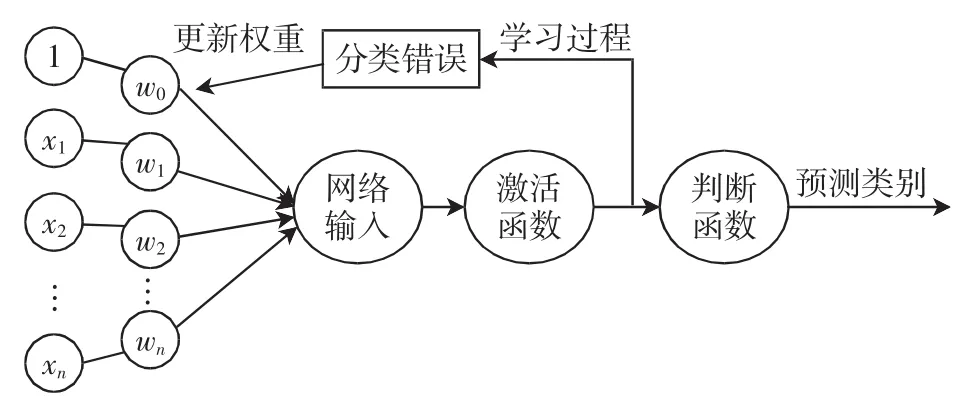
图3 Logistic回归原理简图Fig.3 Schematic diagram of Logistic regression

定义数据：X=[x0，x1，x2，x3…xn]，其中 n 为特征维度.类别标签

网络输入：

式中：W=[w0，w1，w2，w3，…，wn]为权重参数.Logistic 回归的目标即训练出权重参数W使得分类错误率最低.

激活函数：

Logistic回归的学习过程就是不断地更新权重W直到其收敛.传统的Logistic回归参数更新过程为：

式中：σ为学习率；ΔJ（W）为损失函数的梯度.Logistic回归的损失函数被定义为log-likelihood函数的最小值：

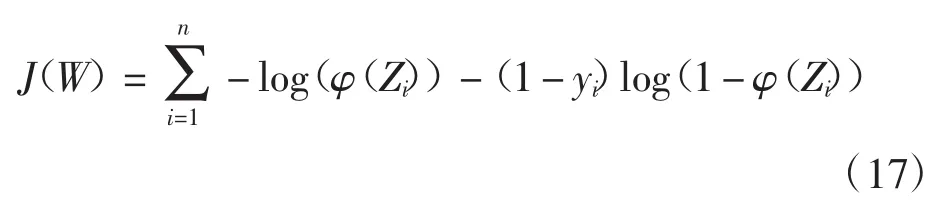
在传统的Logistic回归学习过程中，如何选取合适的σ值成为至关重要的问题，学习率过小会导致收敛过程变慢，需要更多的迭代次数，学习率过大会造成更新过程发散.

然而，在实际应用中，数据中的每个特征对分类的影响是不同的，对影响较大的特征使用较大的学习率势必会造成学习过程中的发散，而对于影响较小的特征使用较小的学习率也会造成更新过程收敛较小.因此，本文提出使用自适应学习权重ϑ=[ϑ1，ϑ2，…，ϑn]重写参数更新过程：

首先计算整体数据集的香农熵：

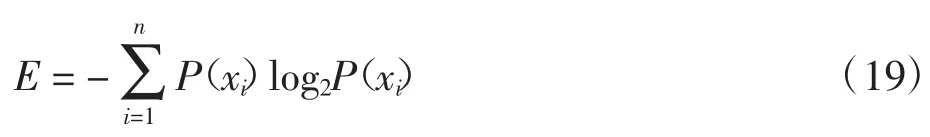
式中：P（xi）为分类标签i的样本数目占总样本数目之比；n为分类标签数目.

对于特征F，遍历整个数据集，寻找F对数据集的最佳划分，使得信息增益IG最大化，信息增益的定义为：

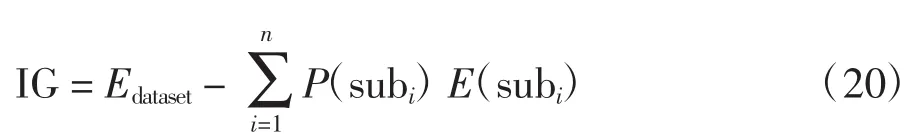
利用 IG 表征特征对分类的影响，[ϑ1，ϑ2，…，ϑn]可由式（21）计算：

3 实验验证

在本次实验过程中，一共采集了不同光强下的53张图片，每张图片有3～10个数量不等的螺钉，用于分类器训练.

3.1 ROI提取结果

已经实验测得每像素代表的实际大小为0.010 4 mm，对于直径为5～8 mm的螺钉，可算出其在图像中的半径大小约为240～385像素.所以设定霍夫圆变换最小检测圆半径为200像素.样片霍夫变换提取结果如图4所示.

图4 样片霍夫变换结果Fig.4 Hough transform result of samples

3.2 Hu矩计算结果

在计算Hu矩之前要先提取螺钉中心纹理处的轮廓，然后计算7个Hu矩，样片中各螺钉的Hu矩如表1所示，单位为像素.

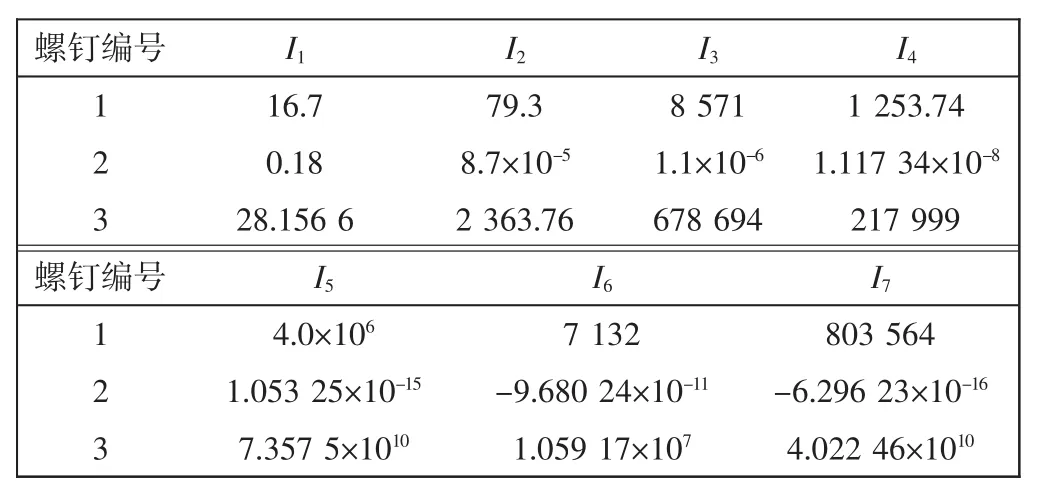
表1 样片中螺钉的Hu矩计算结果Tab.1 Hu moments result of screws in sample

3.3 滑牙缺陷判别处理

首先进行logistic回归分类器的训练，将53张图片共357个螺钉样本分为测试样本与训练样本，计算各特征的最大化信息增益，结果如表2所示.

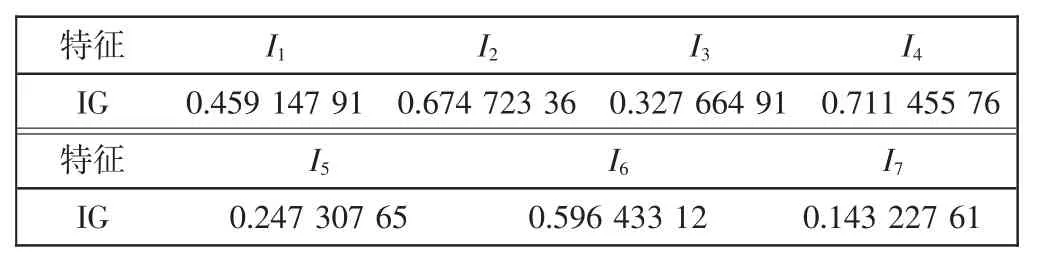
表2 各特征的最大化信息增益Tab.2 Maximization of information gain for each feature

由表 2 可知，I2、I4、I6对螺钉分类的影响较大.然后将最大化信息增益的倒数归一化，作为自适应学习权重.分别取σ=0.1与σ=0.01并迭代500次，作为对比，分别绘制本文提出的自适应学习权重随机梯度下降法与传统的随机梯度下降法的损失函数输出，如图5和图6所示.

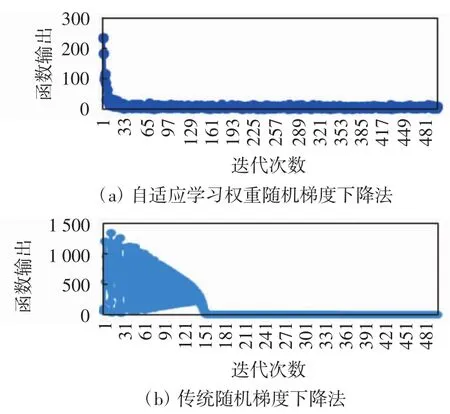
图5 σ=0.01时损失函数输出Fig.5 Loss function output at σ=0.01

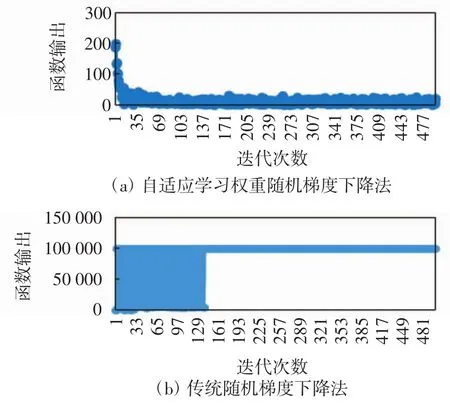
图6 σ=0.1时损失函数输出Fig.6 Loss function output at σ=0.1

由图5和图6可以看出，当学习率取0.01时，传统随机梯度下降法需要迭代151步才能开始收敛，而本文自适应学习权重随机梯度下降法迭代到33步时已经开始收敛，提高了收敛速度；当学习率取0.1时，传统方法因学习率过大而发散，而本文方法迭代到35步时依然能开始收敛.因此，与传统的随机梯度下降法相比，当学习率取值较小时，自适应学习权重随机梯度下降法有更快的收敛速度，同时当学习率取值偏大时也能很好的收敛.

然后用测试样本分别测试训练好的Logistic回归分类器，求出其分类准确度.测试样本集总数为100，基于自适应学习权重随机梯度下降法错分类数为4，准确度为96%.传统随机梯度下降法的Logistic回归分类器错分类数为5，准确率为95%.

4 结论

（1）σ=0.01时，本文提出的改进Logistic回归分类算法迭代33步后开始收敛，而传统方法需迭代151步；σ=0.1时，本文方法需迭代35步后开始收敛，而传统方法因学习率过大而发散.因此，与传统的Logistics回归分类器相比：在选取同样的学习率σ时，本文提出的改进Logistic回归分类算法能更快地收敛，需要较少的迭代次数；对于过大或过小的学习率，在滑牙检测中依然有稳定的迭代收敛次数.

（2）在减少训练过程的迭代次数的同时，本文提出的改进Logistic回归分类算法的分类准确率为96%，而传统的Logistic回归分类算法准确率为95%，二者有着相近的预测准确度.