考虑结合面特性的锭子组合系统固有频率与振型

周国庆 ，杨会会 ，袁汝旺 ，韩 雪 ，蒋秀明 ，罗 孝

（1.天津工业大学机械工程学院，天津 300387；2.天津工业大学天津市现代机电装备技术重点实验室，天津 300387）

锭子和纱管是主要的纺织器材，承担着纱线加捻、卷绕、储运和退绕等任务，其组合系统的振动特性直接影响纺纱质量和效率.锭子组合系统的配合主要是由锭杆锥面和纱管锥面（天眼部分）进行结合[1-2]，并通过摩擦力传递力和力矩，且其结合部的联接性能直接影响系统的动态特性，故建立准确的结合部动力学模型对锭子组合系统的动力学分析至关重要.以往研究主要集中在单个锭子系统建模与分析[3-5]，而对锭子和纱管组合系统研究却相对较少.关秀芬等[6]利用传递矩阵和导纳法研究纺纱锭子组合系统动态特性，但并没有考虑锭子与纱管结合面的动态特性.许多学者利用弹簧-阻尼单元模拟结合面的建模方法分析结合面动态特性[7-9]，Namazi等[7]运用有限元法建立了各均布单元结合部的动力学模型来模拟锥面结合部；汪博和赵万华等[10-11]采用有限元法通过分布式弹簧来模拟结合面的动力学模型，研究结果表明结合面动力学模型可采用弹簧-阻尼单元表达.

针对锭子组合系统结合面磨损对其动态特性的影响，本文采用弹簧-阻尼单元模拟结合面的方法准确建立锭子组合系统的动力学解析模型，且通过对单元面积结合面的刚度和阻尼求积分的方法来计算实际的结合面刚度和阻尼，分析结合面的动态特性，并利用ANSYS对锭子组合系统进行模态分析，得出锭子组合系统的固有频率和振型.

1 锭子组合系统建模

1.1 锭子组合系统结构

锭子组合系统的结构如图1所示，锭子和纱管存在两个结合面2和4，锭杆与纱管天眼结合面2位于纱管顶部，锭子与纱管下底口结合面4位于纱管底部.

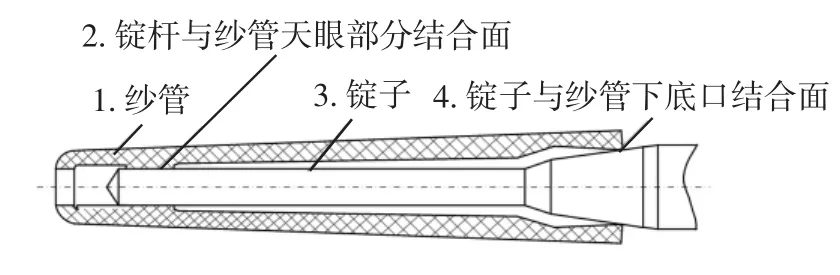
图1 锭子组合系统结构示意图Fig.1 Schematic diagram of spindle combination system

1.2 结合面的动力学建模

锥面是锭子-纱管结合面的主要表现形式，利用均布弹簧-阻尼单元且考虑法向和切向平动以及绕z轴转动的结合面动力学模型如图2所示.

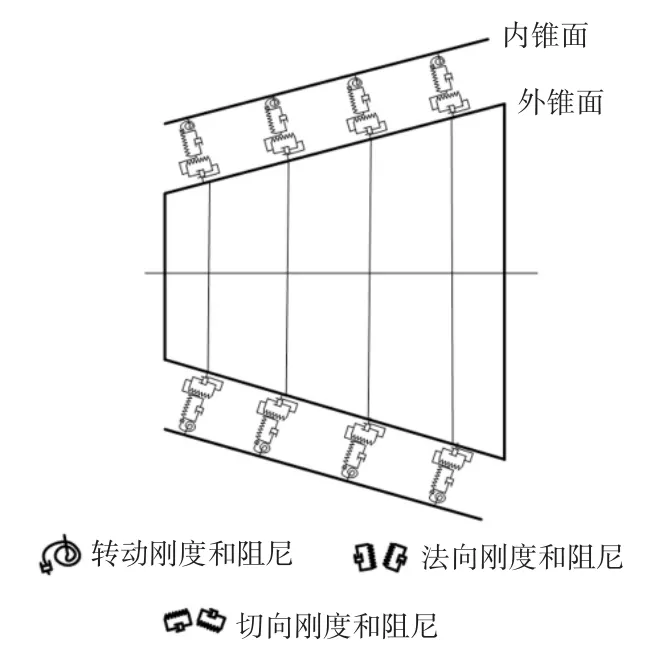
图2 锥面结合部动力学模型Fig.2 Dynamic model of conical joint

利用有限元法将锥面结合面沿锭子轴线方向均分为N段，通过相应的节点对锭子和纱管两部件相互联接，节点处则会发生耦合作用.当锭子和纱管结合面处发生弹性变形时，其对应的节点将会产生相对位移，并伴随着耦合力和耦合力矩的产生，图3所示为简化后结合面处的弹簧-阻尼单元.

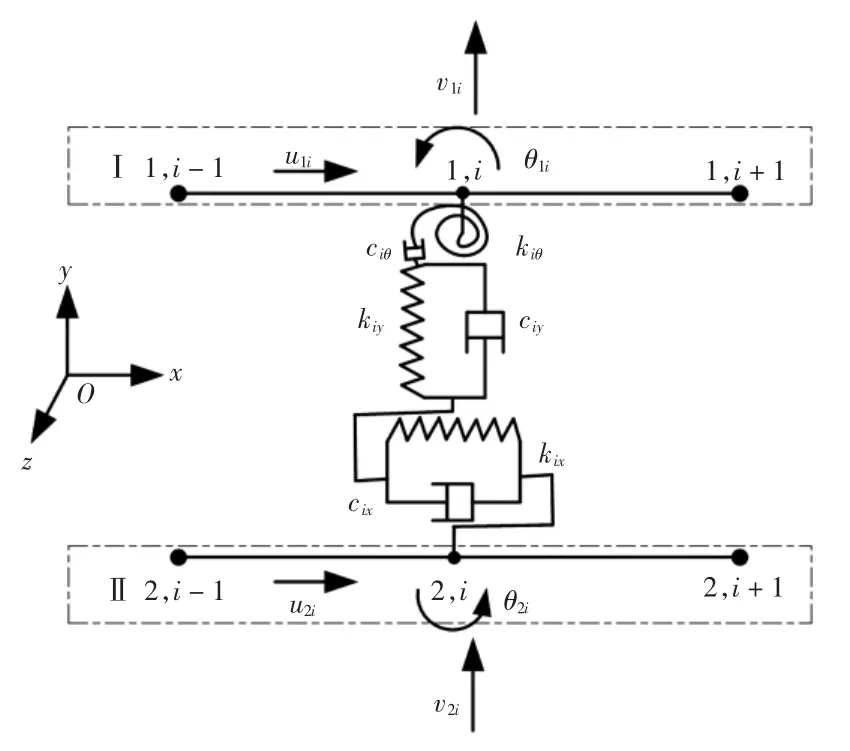
图3 结合面弹簧-阻尼单元Fig.3 Spring-damping unit on joint interface

当部件Ⅰ（纱管）的节点i和部件Ⅱ（锭子）的节点i间发生相对运动时，其耦合力和力矩分别为：

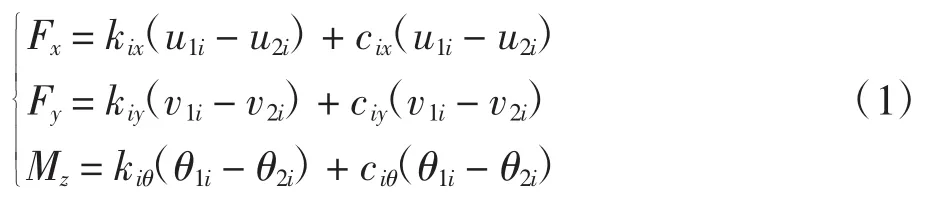
式中：u1i、v1i、θ1i分别为部件Ⅰ的 i节点向 x 向、y 向和绕 z的接触刚度；u2i、v2i、θ2i分别为部件Ⅱ的 i节点向 x向、y 向和绕 z 的接触刚度；kix、viy、θiθ分别为锥面结合面第i段的x向、y向和绕z的接触刚度.

分别求出结合面对应的两个节点间的接触刚度矩阵和阻尼矩阵[11]，并将各个节点的接触刚度矩阵和阻尼矩阵进行组建，得到结合面的总接触刚度矩阵KJ和总阻尼矩阵CJ.

1.3 锭子组合系统动力学建模

锭杆下部双弹性支撑结构的锭子组合系统简化模型[6]如图4所示.

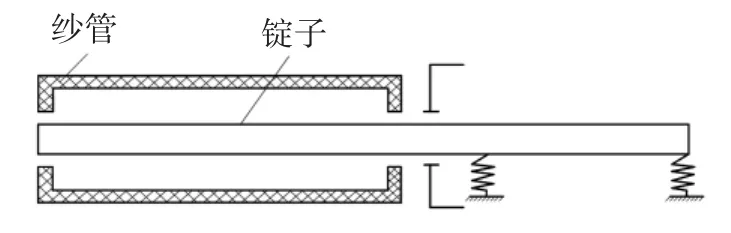
图4 锭子组合系统简化模型Fig.4 Simplified model of spindle combination system

在考虑锭子和纱管结合面的整体刚度矩阵KJ和整体阻尼矩阵CJ的情况下，得到相应的纺纱锭子组合系统转子动力学方程：

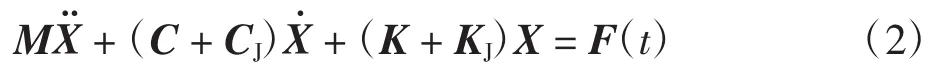
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；X为位移向量；F（t）为激振力列向量.

按照将结合面简化为弹簧-阻尼的建模方法，得到纺纱锭子组合系统简化的动力学模型，如图5所示.

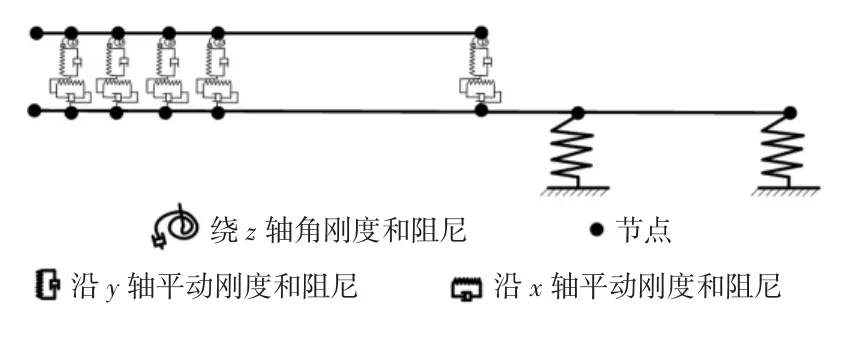
图5 锭子组合系统简化动力学模型Fig.5 Simplified kinetic model of spindle combination system

1.4 结合面接触刚度的确定

1.4.1 结合面法向接触刚度

锭子组合系统锥部结合面处锭子外锥面的受力简图如图6所示.图6中，D1为结合面小端直径；D2为结合面大端直径；L1为结合面接触长度；α为结合面锥角（锭子锥角）.

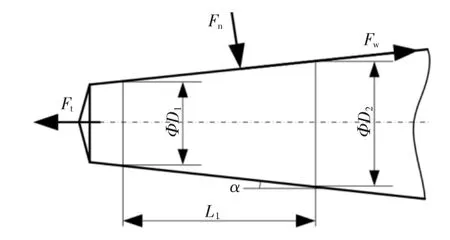
图6 结合面处锭子外锥面受力图Fig.6 Schematic diagram of force at outer surface of spindle on joint interface

由图6可得此时的平衡方程：

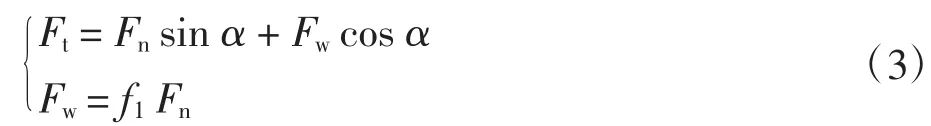
式中：Ft为纱管上跳力；Fn为锭子外锥面正压力；Fw为纱管总握持力；f1为锭子与纱管上支撑处锥部结合面处的摩擦因素.

由式（3）可得锭子外锥面正压力：

锭子-纱管结合面接触面积：

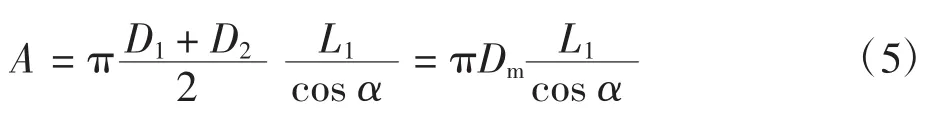
式中：Dm为锭子与纱管锥部结合面处配合中径.

所以结合面处的压强为：

得出结合面处的等效弹簧刚度kn为：

式中：kn为等效弹簧刚度；kn′为单位面积的法向接触刚度；P为平均表面压强；A为接触面积；γ、β均为常数，主要由接触表面的材料、表面粗糙度、表面硬度、表面纹理的相互方向和表面结合误差等综合因素的影响所决定.

将式（5）、（6）代入式（7），得到系统结合面的法向接触总刚度为：

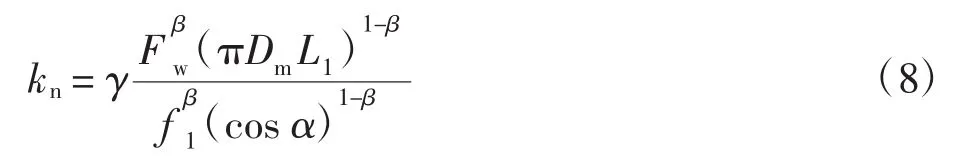
通过以上计算可得出结合面的法向接触总刚度，利用有限元法将长度为L1的接触锥面均分为N段，由于锥体的侧面积不同，因此，计算第i段结合面处的法向接触刚度为：

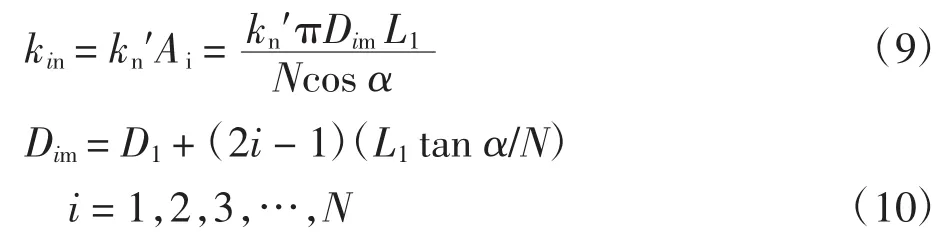
式中：Ai为第i段锥面结合面的接触面积；Dim为第i段锥面结合面的中径；D1为锭子与纱管锥部结合面处的小端直径；α为锭子锥角.

1.4.2 结合面切向刚度

通常结合面的切向刚度系数为法向刚度系数的1/3～2/3，取锭子-纱管结合面的切向刚度kt=kn/2，即ant=0.5，并且在计算中第i段的结合面切向接触刚度计算可在考虑系数ant的情况下根据式（9）进行计算得出.

1.4.3 结合面角刚度

结合面的角刚度计算简图如图7所示.

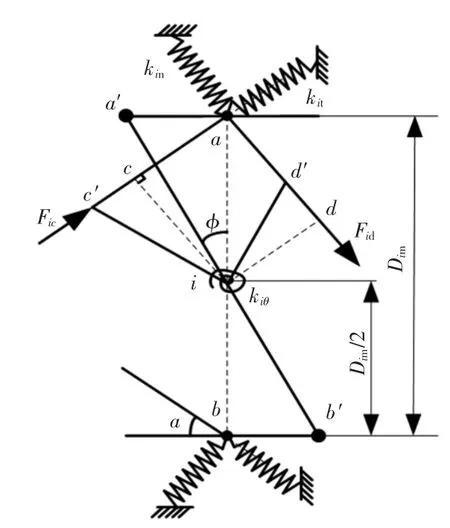
图7 结合面角刚度计算简图Fig.7 Schematic diagram of angle stiffness calculation on joint interface

当划分后的第i段小锥体ab绕i点旋转时，同时由于结合面接触法向刚度kin和结合面切向刚度kit的影响，使得小锥体产生弹性恢复力矩，根据角刚度的计算方法可利用其转角计算角刚度.图7中：Dim为第i段结合面锥面中径；φ为弹性力作用下的偏转角，当转角φ极小时可简化为tan φ≈φ；α为锭子锥角.

由图7可得：

式中：Fic、Mic为 c点弹性恢复力和力矩；Fid、Mid为 d 点弹性恢复力和力矩.

由角刚度kiθ=M/φ，可得出第i段锥体的角刚度为：

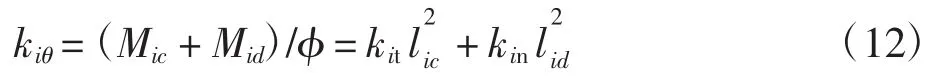
根据几何关系可得：

将式（9）、（10）和式（13）代入式（12），可得第 i段小锥体结合面的接触角刚度为：

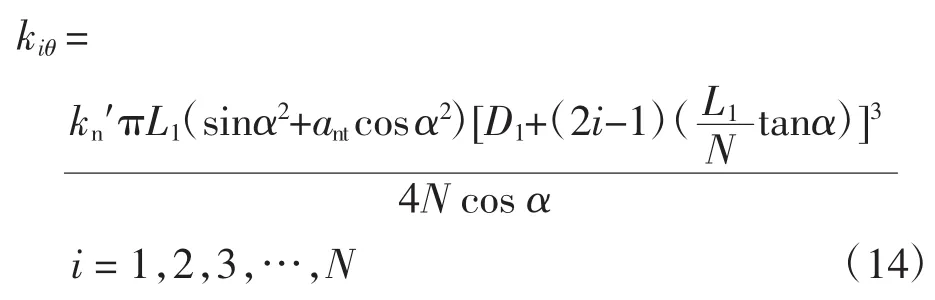
如果此时N→∞时，得出结合面的总角刚度为：

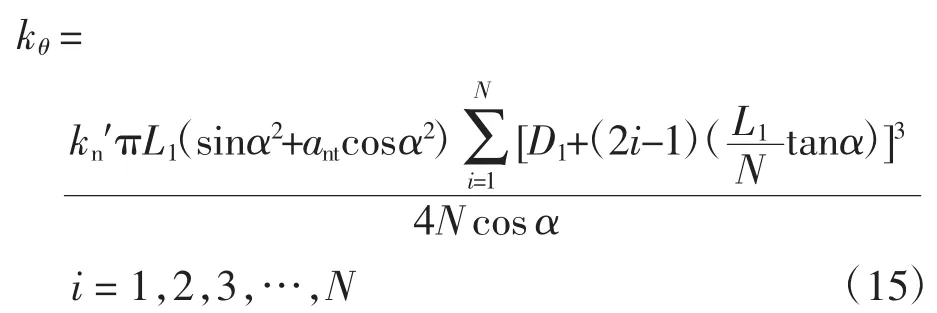
1.4.4 计算阻尼矩阵

为了简化计算，此时采用比例阻尼来计算系统总阻尼矩阵，计算如下：

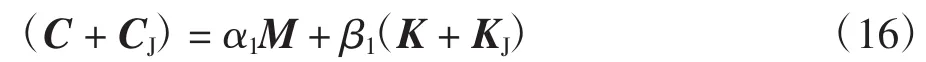
式中：α1、β1均为比例系数，且满足以下关系式：

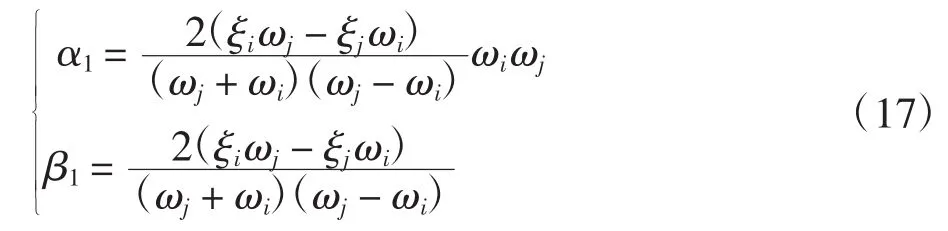
由式（17）可通过任意两个固有频率ωi、ωj和阻尼比 ξi、ξj求出其相应的比例系数 α1、β1，进而得到相应的阻尼矩阵，一般情况下金属和无油结合面的阻尼比的取值范围为0.001～0.100，根据锭子-纱管的工作情况可取为0.001 5.

表1所示为锭子与纱管天眼处结合面的主要结构尺寸和接触刚度计算结果.

表1 锭子-纱管结合面结构参数和结合面接触刚度Tab.1 Structural parameters and contact stiffness of spindle-bobbin joint interface

2 纺纱锭子组合系统仿真分析

由式（4）可得出无阻尼系统的特征方程为：

通过式（18）便可得出锭子-纱管组合系统的各阶固有频率和相应的模态矩阵U.

按图8所示对锭子和纱管模型采用Pro/E三维建模并导入ANSYS，锭子和纱管两个实体的模型参数如表2所示.

图8 锭子组合体实体模型Fig.8 Spindle combination solid model

表2 锭子和纱管实体模型参数Tab.2 Solid model parameters of spindle and bobbin

在ANSYS中对锭子和纱管采用实体单元进行分析，锭子轴承的支撑部分简化为弹性支撑，并且每个轴承的支撑类型简化为沿轴的周向方向等效分布为4个弹簧，如图9所示.用Combin14来模拟各个弹簧，各弹簧长度l=10 mm.

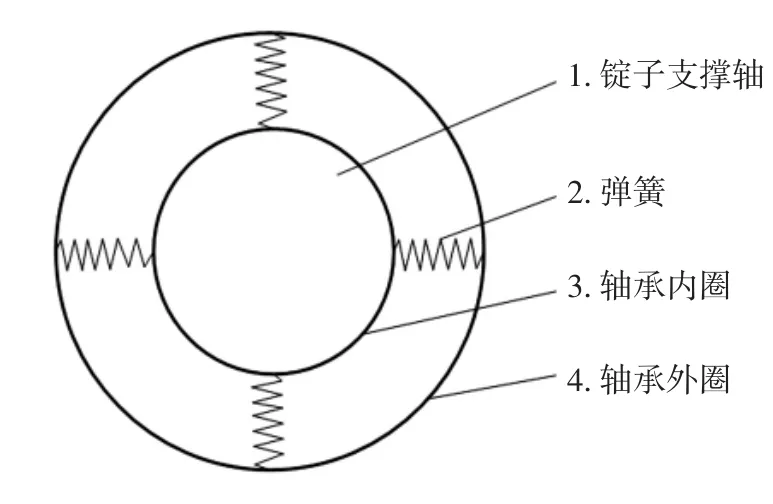
图9 弹性支撑简化模型Fig.9 Simplified model of flexible support

表3、表4分别给出了模型外相应关键点的坐标和相应的上下弹性支撑的刚度.锭子与天眼接触部分沿轴向均分为3段，可看到沿轴向锭子和纱管有4个接触点；锭子和纱管的下结合点处也采用弹簧-阻尼单元连接，得到锭子组合系统简化模型.

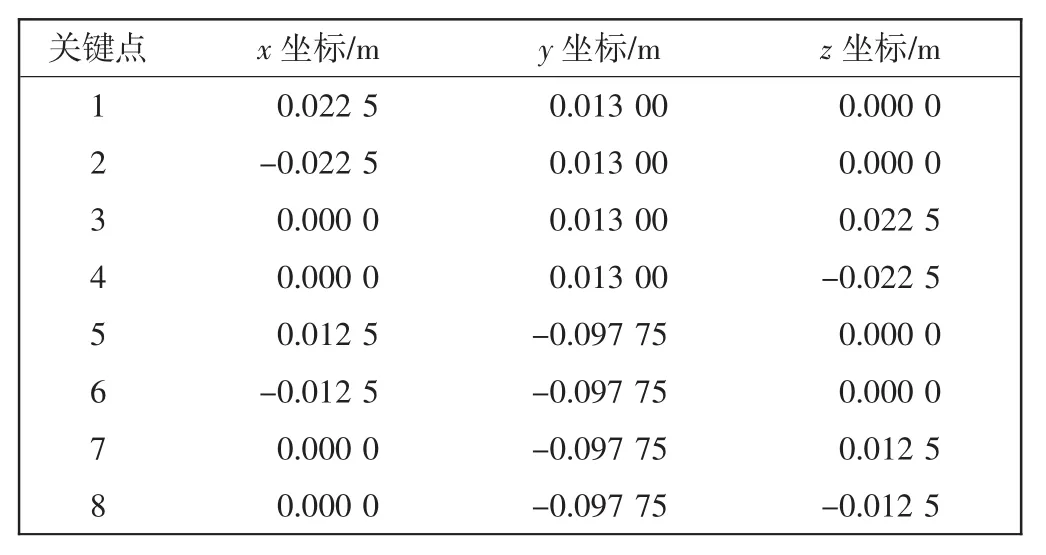
表3 模型外各关键点坐标Tab.3 Coordinates of key points outside model

表4 上下弹性支撑刚度Tab.4 Up and down elastic support stiffness

在ANSYS中对模型进行模态分析求解，提取其前六阶固有频率和振型.通过改变锭子锥面与纱管天眼处沿轴向接触弹簧的段数来模拟其接触面积的改变，其中单侧接触为下底口损坏时结合面2处只存在图9所示的周向1段弹簧接触；且当纱管下底口损坏时（下底口处接触弹簧断开）亦可通过改变下底口与锭子锥面的连接情况来模拟.不同接触情况的锭子组合系统固有频率如表5所示.

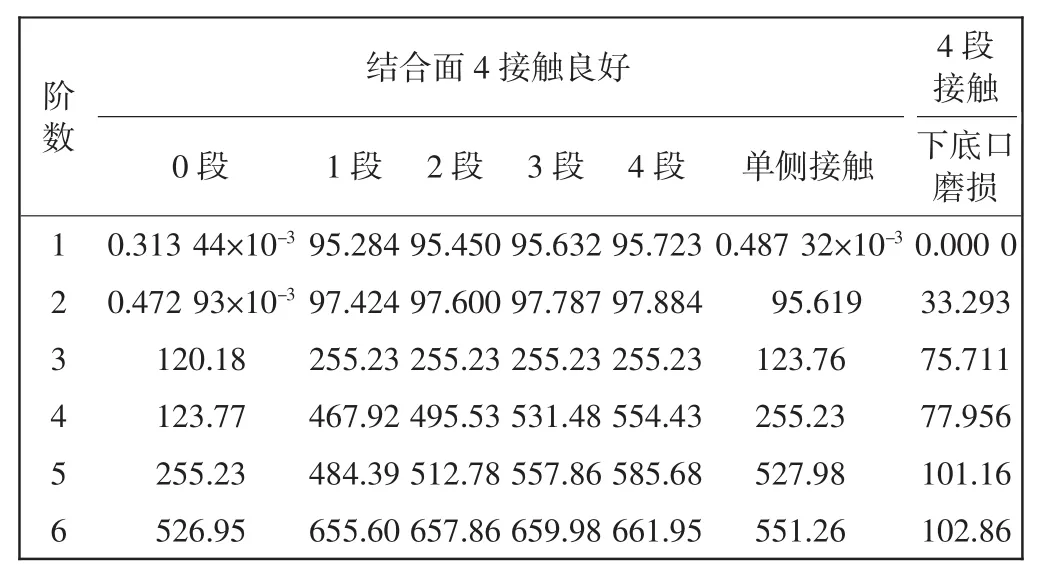
表5 不同接触情况的锭子组合系统固有频率Tab.5 Natural frequency of spindle combination system with different contact conditionsHz

转速和频率的关系：

式中：n为转速（r/min）；f为频率（Hz）.

由表5可知：结合面4接触良好且接触段数相同的情况下，固有频率随着阶数增加而增加，相应的临界转速亦随着阶数的增加逐渐增大，最小的临界转速为下底口损坏时的0 r/min，而最大的临界转速为4段接触时的39 717 r/min；结合面4接触良好且同阶数条件下，固有频率随着接触段数的增加而增加，且1—4段接触的前六阶固有频率相差较小，其中第1阶固有频率的最大误差为0.439 Hz，第2阶固有频率的最大误差为0.46 Hz，第3阶固有频率的最大误差为0 Hz，第4阶固有频率的最大误差为86.51 Hz，第5阶固有频率的最大误差为101.29 Hz，第6阶固有频率的最大误差为6.35 Hz，从其误差可知在前3阶和第6阶时1—4段接触的固有频率十分接近，尤其在3阶时1—4段接触的固有频率相同，而在第5阶和第6阶时1—4段接触的固有频率误差相差较大，说明此时第3阶到第4阶固有频率出现了一个极大的转折.锭子与纱管天眼部存在周向整圈接触时接触面积变化对其组合系统的固有频率影响较小；接触面2的锥面未存在有效接触，其1—2阶固有频率接近0 Hz，3—6阶固有频率明显小于1—4段接触的固有频率，无法满足组合系统对稳定性的要求；周向单侧接触时固有频率与1—4段接触的固有频率存在较大差异；锭子组合系统接触面4接触良好时，结合面2接触及其有效接触面积的大小影响锭子组合系统固有频率，结合面2完全接触时组合系统的固有频率最大，相应的临界转速亦最大.结合面2完全接触且下底口磨损时，1阶固有频率为0 Hz，致使组合系统不稳定，且其2—6阶固有频率与结合面4接触良好的固有频率存在显著差异，结合面4磨损对组合系统的固有频率影响更大.由式（19）可知，结合面2存在1段周向有效接触的3、4阶固有频率所对应的临界转速分别为15 314 r/min和28 075 r/min，而纱管振程检测额定转速为18 000 r/min，介于3、4阶固有频率所对应的临界转速之间，同时额定转速也介于0段接触时的5、6阶固有频率和单侧接触时的4、5阶固有频率所对应的临界转速之间，避免了系统共振.

组合系统的振型与固有频率变化类似，图10—图12给出结合面2、4变化导致的组合系统振型.

由图10可知：结合面4接触良好且结合面2存在周向1段接触时1、2、6阶振型相对位移最大处都为纱管顶部，1—2与4—6阶振型中纱管下部的相对位移都很小，且顶部与底部相对位移偏差较大，易导致细纱断头；锭子额定转速在3—4阶之间，振型相对偏移误差较小，顶部相对位移适中；结合面2的接触面积较小时组合系统的顶部相对位移较大，易产生纱线断头，故在纱管检测中仅需对纱管上部的振幅进行检测，就能很好的判断出纱管的合格与否.

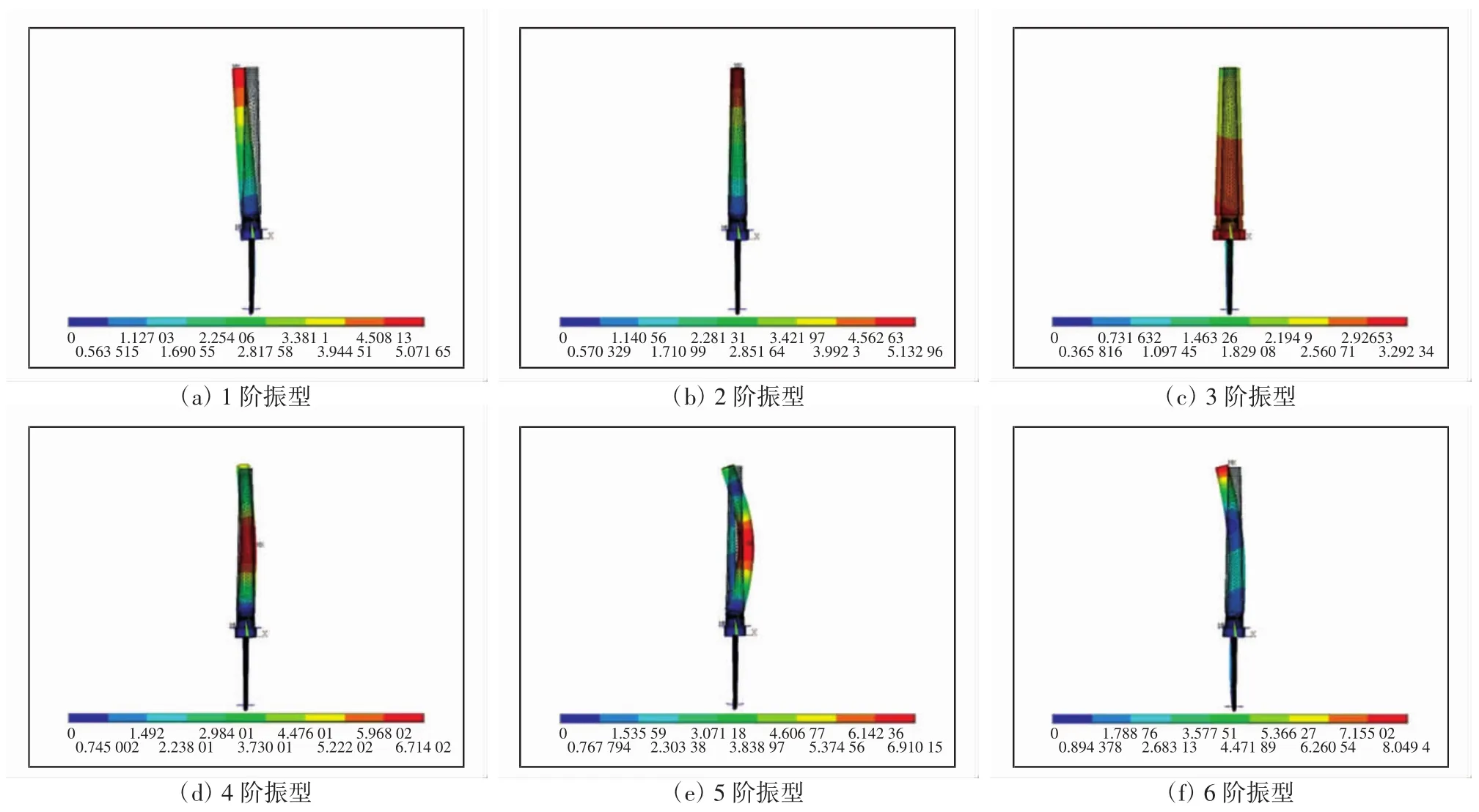
图10 结合面2周向1段接触组合系统振型Fig.10 Modes of combination system as 1 stages of circumferential contact of joint interface

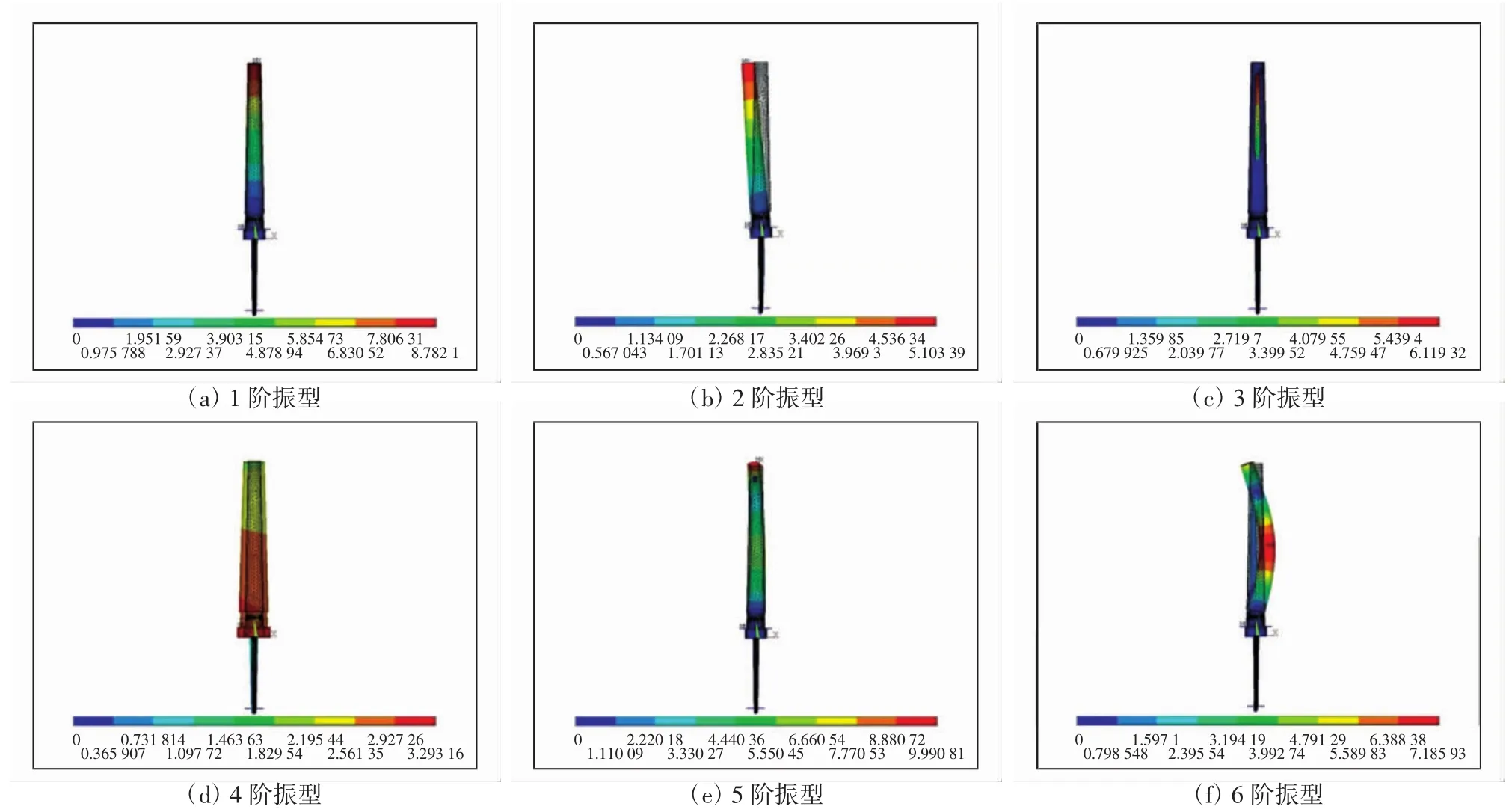
图11 结合面2周向单侧接触时前六阶振型Fig.11 First six order modes as circumferential unilateral contact of joint interface 2

由图11可知：结合面4接触良好且结合面2存在周向单侧接触时1—2、5阶振型相对位移最大处都为纱管顶部，在第1—3、5—6阶振型中纱管底部的相对位移都很小；额定转速在4—5阶之间，且4—5阶振型中纱管顶部的相对位移都较大，故周向作用力不均匀致使纱管相对位移增加，引起纺纱生产过程中的断头和张力波动，不利于高速纺纱，且在纱管检测中仅需对纱管上部的振幅进行检测，就能很好的判断出纱管的合格与否.

由图12可知：结合面2完全接触且结合面4磨损时1阶振型整体相对位移大，且纱管具有向上位移；5—6阶振型相对位移最大处都为纱管顶部，2—4阶振型相对位移最大处都为纱管底部.在结合面2完全接触且结合面4磨损时纱管顶部和底部的相对位移都较大，故结合面4磨损对组合系统的振型影响更大，且额定转速所对应的固有频率并不在1—6阶固有频率和振型范围内，此时对纱管上部的振幅进行检测，也能很好地判断出纱管的合格与否.

图12 下底口损坏时前六阶振型Fig.12 First six order modes as lower bottom is damaged

3 结论

（1）针对锭子组合系统结合面磨损对其动态特性的影响，采用弹簧-阻尼单元来模拟锭子锥面与纱管的结合面，建立锭子与纱管结合面的接触模型和锭子组合系统的动力学模型，为锭子与纱管结构优化和组合系统振动分析提供理论参考.

（2）锭子与纱管的结合面磨损引起的接触面积变化影响锭子组合系统的固有频率，且周向单侧接触比周向完全接触产生的影响大；锭子与纱管下底口结合面磨损对组合系统固有频率的影响比锭子与纱管天眼结合面磨损的影响大；纱管振程检测额定转速为18 000 r/min，不在其固有频率所对应的临界转速上，避免系统共振.

（3）锭子与纱管组合系统结合面磨损加剧振型变化，锭子与纱管下底口结合面接触良好时纱管底部振型的相对位移明显变小，纱管顶部振型的相对位移随着锭子与纱管天眼处的接触面积减小而加剧，但接触面积较小致使纱管整体相对位移较大；锭子与纱管下底口结合面磨损时，纱管底部振型的相对位移明显增大，且其顶部振型的相对位移亦比较大，故在纱管检测时设置对纱管上部进行检测是比较合理的，且结合面磨损引起纱管相对位移增加，增加张力波动，致使纱线断头，不利于纺纱生产过程高速化.