一类解析函数的三阶Hankel行列式
张海燕, 汤 获, 马丽娜
(赤峰学院数学与统计学院,内蒙古赤峰024000)
1 引言及预备知识
设A表示单位圆盘D = {z∈C:|z|<1}内单叶解析且具有如下形式的函数族
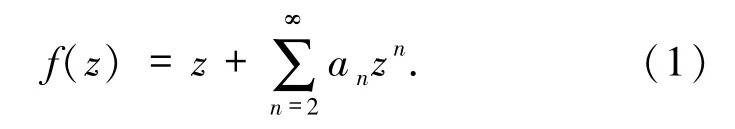
设P表示单位圆盘D内具有如下形式且满足条件 Re p(z)>0的函数族

定义 1[1]设函数 f(z)和 g(z)在单位圆盘 D内解析.如果存在D内的Schwarz函数ω(z)满足:ω(0)=0,|ω(z)|<1 且 f(z)=g(ω(z)),则称 f(z)从属于 g(z),记为 f(z)≺g(z).特别地,如果 g(z)在D上是单叶的,则

2013 年,Bansal[2]研究了函数类(A,B)的二阶Hankel行列式|a2a4|,并得到了其上界估计.
定义 2[2]设(A,B)具有(1)式的形式且满足下述条件的函数全体

其中,-1≤B <A≤1,0≤γ≤1,τ∈C\{0}.1976 年,Noonan等[3]定义了函数f的q阶Hankel行列式

其中,a1=1,n≥1,q≥1.
特别地,有:

因为 f∈A,a1=1,故有

易知,当 μ = 1 时,Fekete 等[4]估计 |a3-|即是|H2(1)|.
近年来,许多学者研究了各类解析函数的二阶Hankel行列式H2(2),得到了其上界估计,详见文献[5-8].对于各种不同的函数类,很多作者进一步对三阶 Hankel行列式H3(1)做出了研究,如文献[9-14].Bansal[2]研究了函数类(A,B)的二阶Hankel行列式|a2a4-|,得到了其上界估计.在此基础上,本文给出了函数类(A,B)的三阶Hankel行列式H3(1)的上界估计,推广了其已有的结果.
2 主要结果
除非特别说明,假设-1≤B<A≤1,0≤γ≤1,τ∈C\{0}.为了证明本文结论,需要如下引理.
引理 1[15]如果 p(z)∈P,则

引理 2[16]如果 p(z)∈P,则存在复数 x 和 z且|x|≤1,|z|≤1,使得

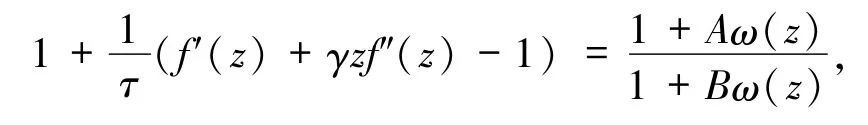
其中,ω(z)是 Schwarz函数且满足 ω(0)=0,|ω(z)|<1,z∈D.令


分别比较(6)式等号两边 z、z2、z3、z4的系数,得:

从而由引理1可得


定理1得证.

证明 由(7)和(8)式可得

设|x|= t,0≤t≤1,c1= c,c∈[0,2],又因为|z|≤1,则由三角不等式及引理2可得
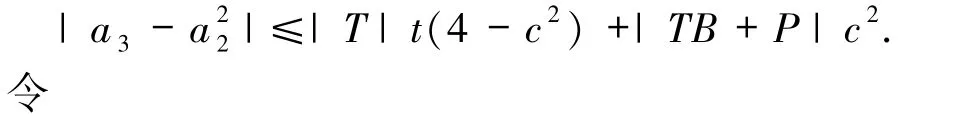
F(c,t)= |T |t(4-c2)+|TB+P |c2,从而有

因此函数 F(c,t)关于变量 t单调递增,故函数F(c,t)在 t=1 处取得最大值,即

进而有 G′(c)= -2c|T|+2c|TB+P|,令G′(c)=0,则有 c=0,或|TB+P|= |T|.下面分 2 种情况讨论.
1)当|TB+P|< |T|时,即有 G′(c)<0,函数G(c)关于 c单调递减,从而 G(c)在 c=0处取最大值,即
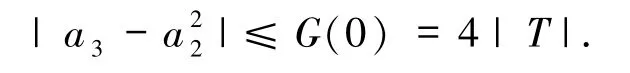
2)类似地当|TB+P|> |T|,此时有 G′(0)>0,则函数 G(c)关于 c单调递增,从而 G(c)在 c=2处取得最大值,从而有函数 F(c,t)在 t=1,c=2 处取得最大值,即|a3-|≤4 |TB+P |.综上可知,定理2得证.
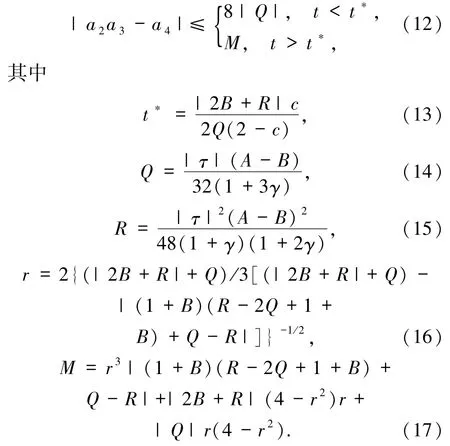
证明 由(7)~(9)式可得

设|x|= t,0≤t≤1,c1= c,c∈[0,2),又因为|z|≤1,则由三角不等式及引理2,可得


1)当 t>t*时,则有∂F/∂t<0,即函数 F(c,t)关于 t单调递减,F(c,t)在 t=0 处取得最大值,即

若 c=0,有 G″(0)= -4|Q|<0,即函数 G(c)在 c=0 处取得最大值,从而可得函数 F(c,t)在 t=0,c=0 处取得最大值,也即|a2a3-a4|≤8|Q|.
2)类似地,当0 <t<t*时,有∂F/∂t>0,即函数F(c,t)关于 t单调递增,F(c,t)在 t=1 处取得最大值,即
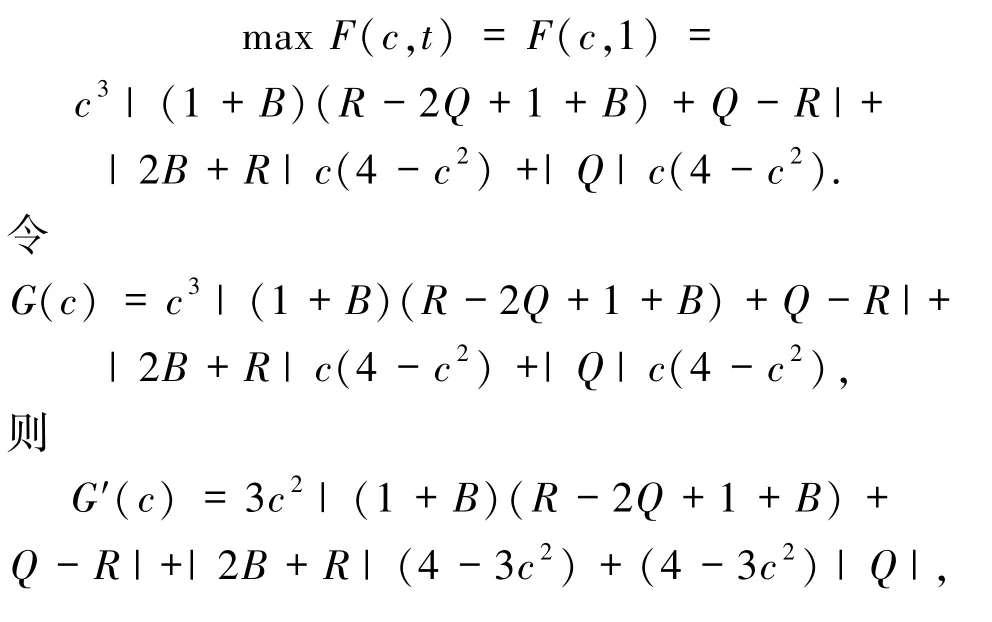

因为 G″(r)<0,所以函数 G(c)在 c=r处取得最大值.综上可知,函数 F(c,t)在 t=1,c=r处取得最大值,从而有

t*、Q、M 分别由(13)、(14)和(17)式给出.
证明 因为


将(3)~(5)、(11)、(12)和(18)式代入到(19)式中,即得定理5.

